1 Worum geht es?

Eine Ellipse sei durch fünf Punkte A, B, C, D, E gegeben (Abb. 1).

Abb. 1: Kegelschnitt durch fünf Punkte

Gesucht sind die Brennpunkte der Ellipse. Gibt es ein Verfahren ohne Rechnen?

Bemerkung 1: Durch fünf Punkte kann auch eine Hyperbel oder eine Parabel gegeben sein.

Bemerkung 2: Wir werden im Folgenden mit Tangenten an die Ellipse in Ellipsenpunkten arbeiten. Dazu gibt es eine Konstruktion [1], die wir im Folgenden als Makro verwenden.

Bemerkung 3: In den Abbildungen ist jeweils die Ellipse magenta eingezeichnet. Dies hat aber rein dekorative Bedeutung. Die Ellipse wird für die Konstruktionen nicht verwendet.

Bemerkung 4: Im Folgenden wird das Konstruktionsverfahren beschrieben. Die Beweise überlassen wir dem der Lust hat.

2 Konstruktionsverfahren

Es sei F der Mittelpunkt der Strecke AB und G der Pol der Geraden AB. Dieser Pol ist der Schnittpunkt der Tangenten in A und B (Abb. 2). Die Gerade FG ist eine Achse der Ellipse.

Abb. 2: Achse

Der Begriff Achse ist hier so zu verstehen: Die Gerade FG ist Spiegelachse der Ellipse bei Schrägspiegelung parallel zur Geraden AB. Sie verläuft durch den Mittelpunkt der Ellipse.

Mit Hilfe einer zweiten Achse finden wir den Mittelpunkt M der Ellipse (Abb. 3).

Abb. 3: Mittelpunkt der Ellipse

Wir tragen das geometrische Mittel (Kathetensatz oder Höhensatz) der Strecken MF und MG von M aus ab. Der Endpunkt N liegt auf der Ellipse. Mit MN haben wir also einen Halbmesser der Ellipse.

Abb. 4: Geometrisches Mittel

Die Richtung des zum Halbmesser MN konjugierten Halbmessers ist parallel zu AB (Abb. 5).

Abb. 5: Richtung des konjugierten Halbmessers

Wir schneiden die Trägergerade des konjugierten Halbmessers einerseits mit der Parallelen zu ersten Halbmesser durch A (Schnittpunkt K) und andererseits mit der Tangenten in A (Schnittpunkt L). Mit Hilfe des geometrischen Mittels der Strecken MK und ML finden wir den Endpunkt O des zweiten Halbmessers.

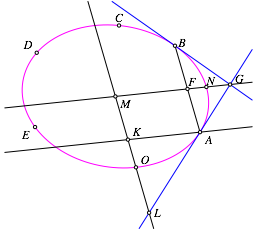
Abb. 6: Konjugierter Halbmesser

Damit haben wir zwei konjugierte Halbmesser und können mit dem Verfahren von Rytz die Hauptachsen und die Brennpunkte der Ellipse konstruieren.

Ein Verfahren ohne Tangenten findet sich in [2]

Websites

[1] Hans Walser: Tangente an Kegelschnitt (14. 2. 2017)

www.walser-h-m.ch/hans/Miniaturen/T/Tangente_an_Kegelschnitt/Tangente_an_Kegelschnitt.htm

[2] Hans Walser: Brennpunkte an Ellipse (14. 2. 2017)

www.walser-h-m.ch/hans/Miniaturen/B/Brennpunkte_Ellipse/Brennpunkte_Ellipse.htm