Hans Walser, [20040320a]
Zerlegungen des Zwšlfeckes / Dissections of the Dodekagon
1 Spielregeln
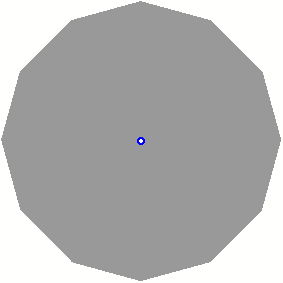
RegelmŠ§iges Zwšlfeck
1.1 Gleichschenklige Dreiecke
Das regelmŠ§ige Zwšlfeck soll in gleichschenklige Dreiecke mit den Spitzenwinkeln 30¡, 60¡ (gleichseitiges Dreieck), 90¡ (halbes Quadrat), 120¡ oder 150¡ zerlegt werden. Die Grš§e der Dreiecke spielt keine Rolle.
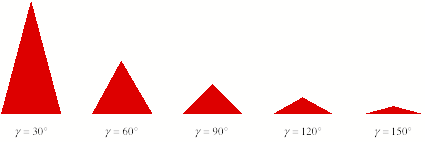
Die Bauteile
1.2 Erweitertes Sortiment
Aus zwei kongruenten
gleichschenkligen Dreiecken kšnnen wir einen Rhombus zusammensetzen. Es ist
daher sinnvoll, auch diese Rhomben als direkte Bauteile zuzulassen. Wir haben
dann Rhomben mit den spitzen Winkeln 30¡ und 60¡ sowie das Quadrat. Dreiecke
mit 
und 
ergeben Rhomben
derselben Form, ebenso Dreiecke mit 
und 
.
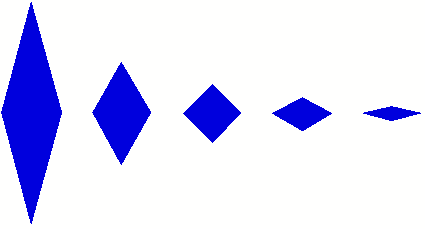
Rhomben
Aus sechs gleichseitigen Dreiecken lŠsst sich das regelmŠ§ige Sechseck zusammensetzen. Auch dieses soll ein zulŠssiger Bauteil sein.
Sechseck
2 Beispiele
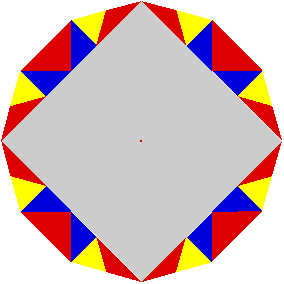
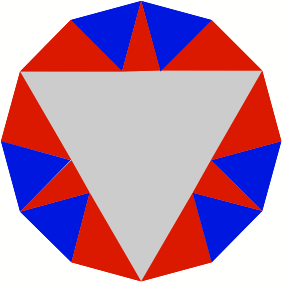
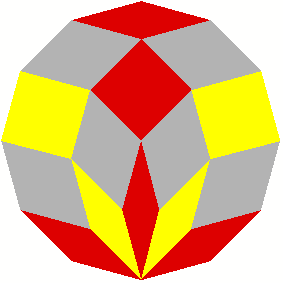
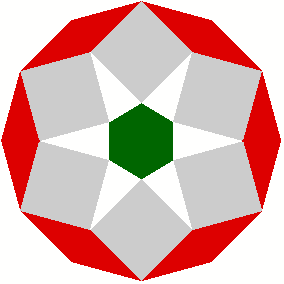
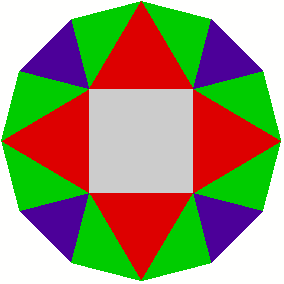
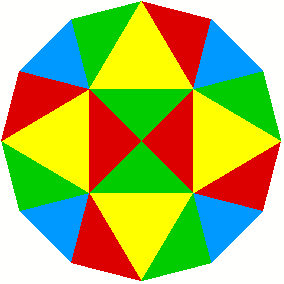
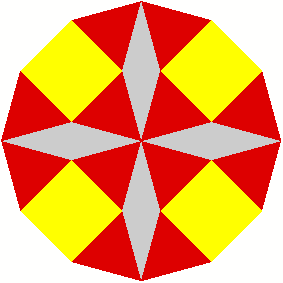
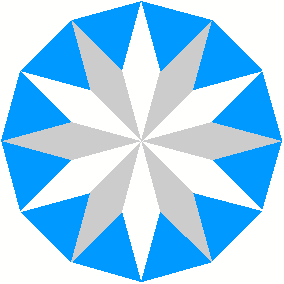
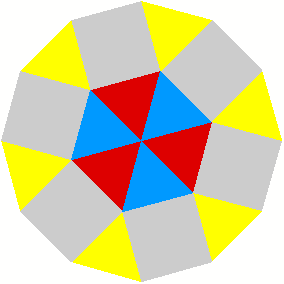
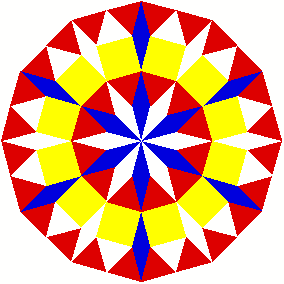
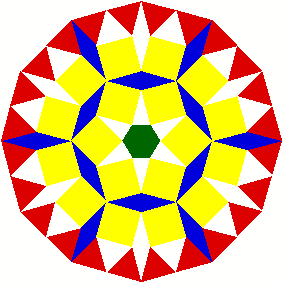
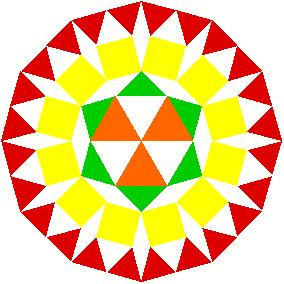
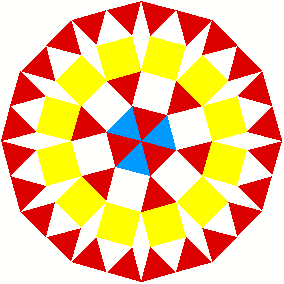
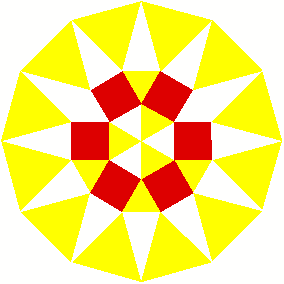
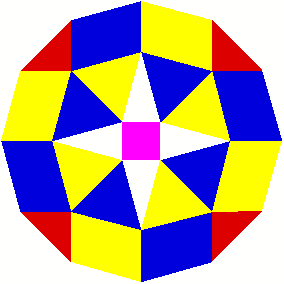
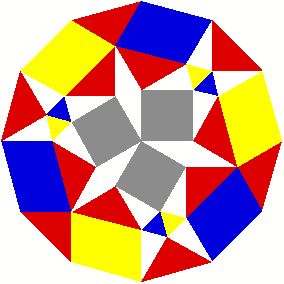
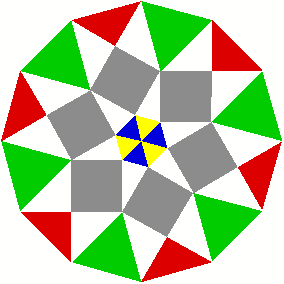
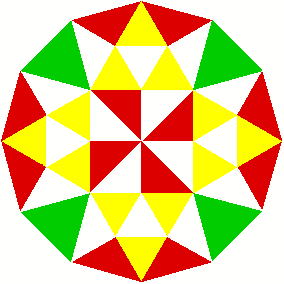
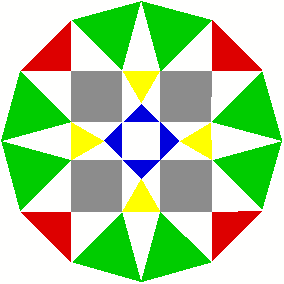
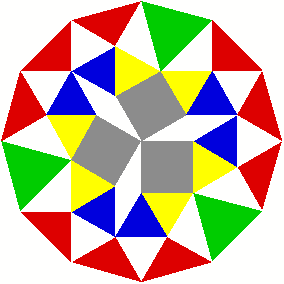
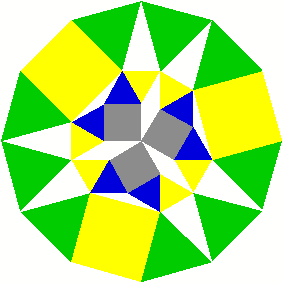
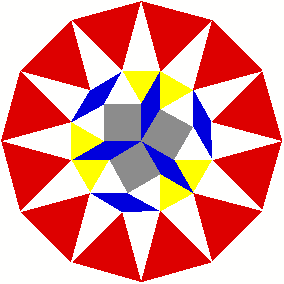
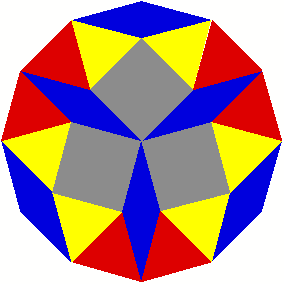
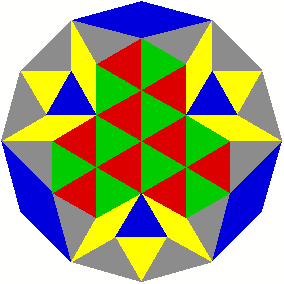
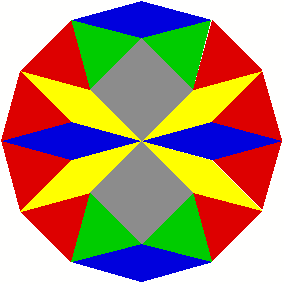
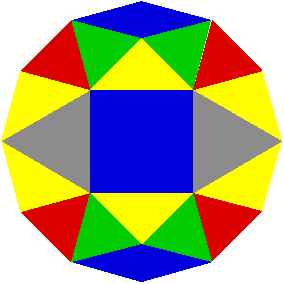
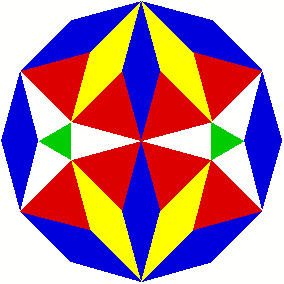
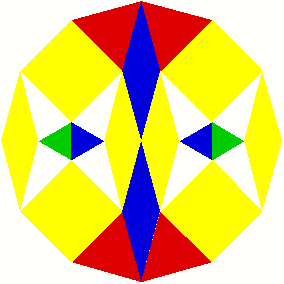
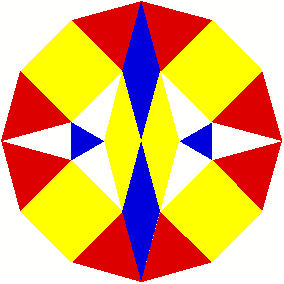
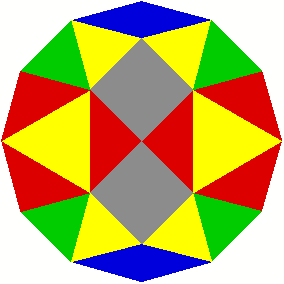
3 Kommentierte Beispiele
3.1 Sonderformen
3.1.1 Spezielles Parallelogramm
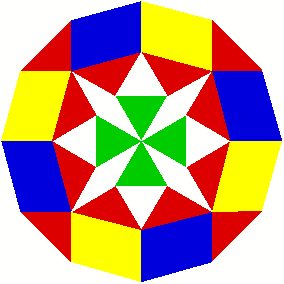
Wie steht es mit den Parallelogrammen?
Wir erhalten
Parallelogramme mit dem SeitenverhŠltnis 
und dem spitzen
Winkel 75¡. Ein solches Parallelogramm lŠsst sich aus unseren Bauteilen
zusammensetzen.
Zusammensetzung des Parallelogramms
3.1.2 Konkaves Viereck
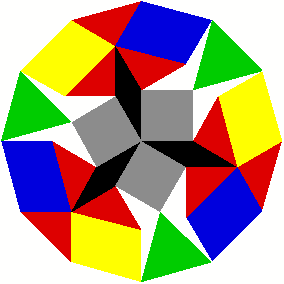
Wie ist es mit den wei§en konkaven Vierecken?
Das konkave Vierreck lŠsst sich aus unseren Bauteilen zusammensetzen.
Zusammensetzung des konkaven Viereckes
3.1.3 45¡-60¡-75¡-Dreieck
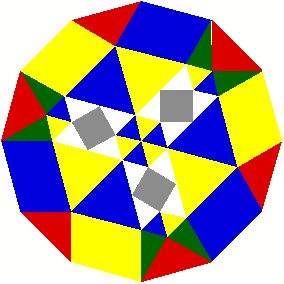
Zerlegung der wei§en Dreiecke?
Die ausgesparten wei§en Dreiecke haben Winkel von 45¡, 60¡ und 75¡ und kšnnen zerlegt werden:
Zerlegung eines 45¡-60¡-75¡-Dreieckes
3.1.4 30¡-45¡-105¡-Dreieck
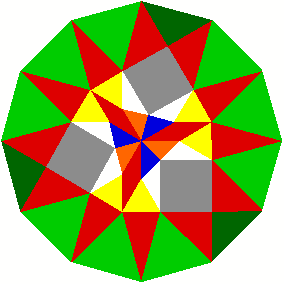
Zerlegung der wei§en Dreiecke?
Die ausgesparten wei§en Dreiecke haben Winkel von 30¡, 45¡ und 105¡ und kšnnen zerlegt werden:
Zerlegung eines 30¡-45¡-105¡-Dreieckes
3.2 Zwšlfeck mit Diagonalen
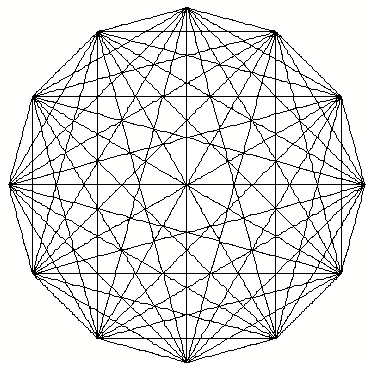
Zwšlfeck mit sŠmtlichen Diagonalen
Im regelmŠ§igen Zwšlfeck zeichnen wir alle Diagonalen ein. Lassen sich alle Teile durch unsere Bauteile zusammensetzen?
3.3 Bild des 6D-WŸrfels
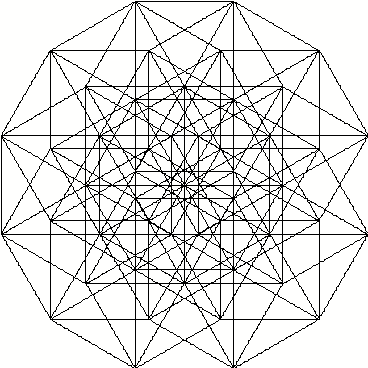
6-D-WŸrfel in isometrischer Darstellung
Der Umriss der isometrischen Darstellung des sechsdimensionalen WŸrfels ist ein regelmŠ§iges Zwšlfeck. Lassen sich alle Teile durch unsere Bauteile zusammensetzen?
3.4 Unendliche Folgen
3.4.1 HŠufungspunkt bei 12 Uhr
HŠufungspunkt im Uhrpunkt 12
In der oberen HŠlfte lŠsst sich ein halb so gro§es regelmŠ§iges Zwšlfeck aussparen und mit einer farblich verŠnderten halb so gro§en Kopie des ursprŸnglichen Zwšlfeckes fŸllen. Der Prozess kann theoretisch ad infinitum iteriert werden. Wir erhalten eine Ausschšpfung des Zwšlfeckes mit unendlich vielen Teilen.
3.4.2 HŠufungspunkt im Zentrum
3.4.2.1 Schšnes Beispiel
HŠufungspunkt im Zentrum
Hier genŸgt es, einen
den Šu§ersten Kranz mit zwšlf Dreiecken zu zeichnen und dann eine verkleinerte
Kopie im Loch einzusetzen. Der Verkleinerungsfaktor c ist 
. Die ausgesparten wei§en Dreiecke sind gleichseitig. Die
sichtbaren Spiralen sind diskretisierte logarithmische Spiralen.
3.4.2.2 Subtiles Beispiel
Wie steht es mit dem ausgesparten wei§en Dreieck?
In diesem Beispiel ist
das ausgesparte wei§e Dreieck zu studieren. Es hat zunŠchst die Seiten 
und 
sowie den Winkel
. Mit Hilfe des Kosinussatzes erhalten wir 
; c ist die positive
Lšsung der quadratischen Gleichung 
. Dies ist auch der Verkleinerungsfaktor von einem Kranz zum
nŠchst inneren Kranz. FŸr die Winkel erhalten wir, was die Zeichnung suggeriert,
nŠmlich 
und 
. Dieses 30¡-145¡-15¡-Dreieck lŠsst sich aus unseren
Bauteilen zusammensetzen.
Zusammensetzung eines wei§en Deieckes
3.5 Fraktal
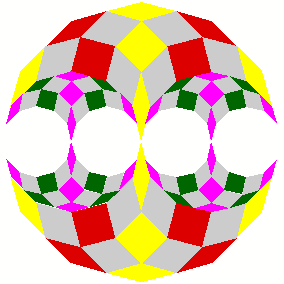
Beginn eines Fraktales
Wenn wir an mehreren Orten aussparen und verkleinerte Kopien einsetzen, entsteht ein Fraktal. In der Praxis ergeben sich Speicherprobleme.
4 Das Zwšlfeck
4.1 Einfache Konstruktion
In einem Karoraster zeichnen wir einen Kreis mit geradzahligem Radius. Damit erhalten wir die Uhrpunkte 3, 6, 9 und 12. Der Schnitt des Kreises mit den Mittelsenkrechten der waagerechten und senkrechten Radien liefert die restlichen Uhrpunkte 1, 2, 4, 5, 7, 8, 10 und 11.
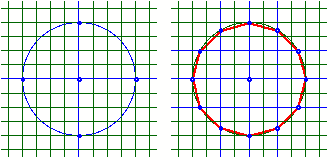
Konstruktion
4.2 FlŠcheninhalt
Ein Zwšlfeck mit dem
Umkreisradius r hat den FlŠcheninhalt 
. Dies kann mit Zerlegungsgleichheit gezeigt werden.
Zerlegungsgleichheit
Bei dieser Zerlegung werden 30¡-60¡-90¡-Dreiecke und 15¡-75¡-90¡-Dreiecke verwendet. Diese kšnnen aber auch aus unseren Bauteilen zusammengesetzt werden.
Zusammensetzung aus Bauteilen
5 Zeichentechnik
Die Figuren kšnnen mit dynamischer Geometrie-Software gezeichnet werden. Mit Vorteil generiert man fŸr die Bauteile Makros in mehreren Farben.
Zerlegungen des Zwšlfeckes / Dissections of the Dodekagon........................................... 1
1 Spielregeln................................................................................................................. 1
1.1 Gleichschenklige Dreiecke................................................................................. 1
1.2 Erweitertes Sortiment......................................................................................... 2
2 Beispiele.................................................................................................................... 3
3 Kommentierte Beispiele........................................................................................... 26
3.1 Sonderformen.................................................................................................. 26
3.1.1 Spezielles Parallelogramm....................................................................... 26
3.1.2 Konkaves Viereck................................................................................... 27
3.1.3 45¡-60¡-75¡-Dreieck............................................................................... 28
3.1.4 30¡-45¡-105¡-Dreieck............................................................................. 29
3.2 Zwšlfeck mit Diagonalen................................................................................. 30
3.3 Bild des 6D-WŸrfels........................................................................................ 31
3.4 Unendliche Folgen........................................................................................... 32
3.4.1 HŠufungspunkt bei 12 Uhr...................................................................... 32
3.4.2 HŠufungspunkt im Zentrum..................................................................... 33
3.5 Fraktal.............................................................................................................. 35
4 Das Zwšlfeck.......................................................................................................... 35
4.1 Einfache Konstruktion..................................................................................... 35
4.2 FlŠcheninhalt.................................................................................................... 36
5 Zeichentechnik......................................................................................................... 36
Inhalt................................................................................................................................ 37