Definition:

Sei W eine ebene Punktwolke aus mindestens drei Punkten, die nicht alle auf einer Geraden liegen. Die Ellipsen mit der Gleichung ( Kovarianzmatrix) sowie ihre Trans-lationen heißen Streuellipsen von W. Die Ellipse mit heißt "Standardstreuellipse".

Aus der Definition folgt, dass . Die Ellipsen sind also wohldefiniert.

Satz: Die Steiner-Ellipsen eines Dreiecks sind Streuellipsen.

Beweis:

Jedes ebene Dreieck kann mit Ähnlichkeitsabbildungen auf ein Dreieck mit den Eckpunkten mit abgebildet werden. Es genügt also, die Behauptung für dieses Dreieck zu zeigen. Sein Schwerpunkt ist. Es gilt:

, , .

Für ist das Dreieck gleichseitig. Seine Steiner-Innenellipse ist aus Symmetriegründen der Innenkreis: . Die Umellipse ist: .

Die durch gegebene affine Abbildung bildet das gleichseitige Dreieck auf

das Dreieck ab. Der Innenkreis geht dabei in die Steiner-Innenellipse über.

Die Umkehrabbildung ist gegeben durch: .

Einsetzen in die Kreisgleichung ergibt:

Diese Ellipsengleichung wird umgeformt:

Andererseits gilt für die Streuellipsen:

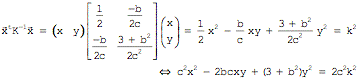
Der Vergleich zeigt: Die Streuellipse für ist die Innenellipse.

Streckung mit dem Faktor 2 ergibt für die Umellipse. ÿ

Korollar: Zu jeder Punktwolke W gibt es Steiner-Ellipsen.

Streuellipsen sind die Ortskurven der Punkte mit Mahalanobis-Abstand vom Zentrum.