2Koecher S

Orthogonale Regression und Streuellipsen

Zu einem Dreieck gibt es unendlich viele Ellipsen, die die Dreiecksseiten von innen berühren. Die flächengrößte dieser Ellipsen ist die Steiner-Innenellipse¹. Die dazu duale Umellipse ist die flächenkleinste Ellipse durch die Eckpunkte des Dreiecks:

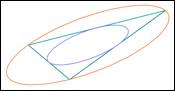
Abb.1: Steiner-Innenellipse und -Umellipse eines Dreiecks

Es zeigt sich, dass die Steiner-Ellipsen zu einer Ellipsenschar gehören, die zu beliebigen ebenen Punktwolken durch Hauptachsentransformation berechnet werden kann. Die statistischen Begriffe Varianz und Kovarianz zeigen dabei eine geometrische Bedeutung.

Abb. 2: Punktwolke: PISA-Ergebnisse oder elliptische Galaxie?

Die Punktwolke sei (ohne Einfluss auf Varianz und Kovarianz) bereits so verschoben, dass der Schwerpunkt im Koordinatenursprung liegt: .

Die Punkte der Wolke seien in Polarkoordinaten gegeben:

Die Kovarianz sei , die Varianzen bzw. .

Wir betrachten eine Ursprungsgerade mit dem Steigungswinkel .

Für jeden Punkt der Wolke gilt dann folgende Überlegung:

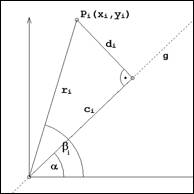
Abb. 3: Projektion auf Ursprungsgerade

Es ist:

und analog:

Die Ursprungsgerade wird im folgenden so bestimmt werden, dass sie eine Extremaleigenschaft in Bezug auf Varianz und Kovarianz der Punktwolke erfüllt.

Sie wird sich später als Hauptachse der gesuchten Ellipsenschar erweisen.

Wir definieren nun die beiden Funktionen:

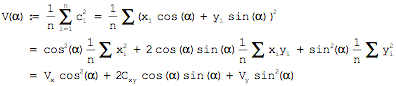
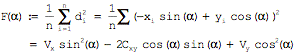
ist der mittlere Flächeninhalt "orthogonalen" Quadrate:

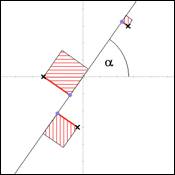
Abb. 4: Quadrate der Lote

Dazu analog ist ist die Varianz der auf der Gerade liegenden Punkte:

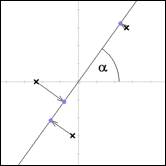
Abb. 5: Varianz der projizierten Punkte

Die Funktion stellt eine Verallgemeinerung der Varianz dar, denn es gilt:

und

Die Funktionen V und F sind um gegeneinander phasenverschoben: .

Wegen gilt:

Daraus ergibt sich . Einem Maximum der (nichtkonstanten) Funktion entspricht daher ein Minimum von und umgekehrt.

Berechnung der Extrema:

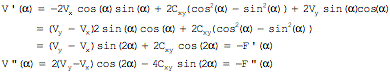
und daher (für )

Für erhält man . Im folgenden gelte:

Im Intervall gibt es eine Maximumstelle und eine Minimumstelle.

Anders als bei den gebräuchlichen Regressionsgeraden werden hier nicht die senkrecht bzw. waagerecht gemessenen Abstände in der Quadratsumme zum Minimum gemacht sondern die orthogonal gemessenen. Man könnte daher von "orthogonaler Regression" sprechen.

Es bezeichne den Winkel

und

Der Test mit der zweiten Ableitung ergibt: ,

wobei das negative Vorzeichen für gilt.

Man erhält für :

Anderenfalls gelten die umgekehrten Zuordnungen.

Beispiel: . Es gilt: , , , , und, da , ,

Die Extremwerte werden später unter Verwendung des Matrizenkalküls berechnet.

Genau wie beim Übergang von der Varianz zur Standardabweichung im Eindimensionalen sollte man auch bei und die Wurzel ziehen. Man erhält dadurch Maßstabsinvarianz und die richtigen Einheiten. In Polarkoordinaten und mit den Daten aus dem Beispiel ergibt sich:

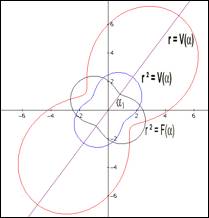
Abb. 6: Graphen zu , und

Betrachten wir die Ursprungsgerade mit Steigungswinkel (wegen ), die durch die "Taille" der zu gehörigen Kurve und gleichzeitig durch die Scheitelpunkte von verläuft. Der Winkel ist nunmehr so bestimmt, dass die Summe der in Abb. 4 dargestellten Abstandsquadrate der Punkte von dieser Gerade minimal ist: . Entsprechend liest man an der zu V gehörigen Kurve ab, dass die in Richtung der Geraden entsprechend gemessene Varianz maximal ist, d.h. .

Darstellung mit Quadratischen Formen

Die Kovarianzmatrix hat die Determinante .

Wegen der Ungleichung von Cauchy-Schwarz gilt ohnehin: .

Im Falle der Gleichheit würde für den Korrelationskoeffizienten folgen:

Daraus ergäbe sich, dass alle Punkte auf einer (steigenden oder fallenden) Gerade lägen.

Fordert man, dass die Punktwolke aus Punkten besteht, die nicht alle auf einer Geraden liegen, ergibt sich als Mindestanzahl 3 sowie, dass .

Daraus folgt, dass die Kovarianzmatrix positiv definit ist.

Man erhält dadurch die positiv definite quadratische Form

In Polarkoordinaten:

Gleichheit tritt nur für bzw. ein. Hält man den Winkel fest, so wachsen die Funktionswerte quadratisch mit . Die quadratische Form kann also als Paraboloid mit Scheitelpunkt im Koordinatenursprung dargestellt werden.

Jeder Schnitt mit einer Ebene, die die z-Achse enthält, ist eine Parabel:

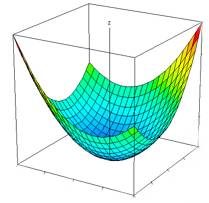
Abb. 7: Darstellung von

Hauptachsentransformation

Bei den Niveaulinien von handelt es sich um Ellipsen:

Beweis: Um den "gemischten" Term in zu eliminieren, führt man mit Hilfe der Drehmatrix

und der Substitution neue Koordinaten ein:

Das Produkt der in der Mitte stehenden drei Matrizen wird explizit ausgerechnet zu

(*)

Für die Winkelund nimmt diese Matrix Diagonalgestalt an. Zur Vereinfachung der Darstellung sei im folgenden und vorausgesetzt. Man erhält die Matrix

Die Berechnung der Extremwerte in der Hauptdiagonalen erfolgt nun nicht etwa numerisch über das Einsetzen des berechneten Winkels in die trigonometrischen Funktionen sondern nach den Rechenregeln für Determinanten. Es gilt nämlich einerseits, dass das Produkt der gesuchten Extremwerte bekannt ist:

Andererseits ergibt die Addition der in der Hauptdiagonale von (*) stehenden Terme

wegen die ebenfalls bekannte Summe

Die Werte , sind daher die Lösungen der quadratischen Gleichung

Es handelt sich um die charakteristische Gleichung der Kovarianzmatrix.

Die gesuchten Extremwerte sind also die Eigenwerte der Kovarianzmatrix:

Die Eigenwerte sind beide positiv und (falls ) voneinander verschieden.

Als Bezeichnung sei vereinbart. Die zugehörigen Eigenvektoren sind:

Die zum Wert gehörige Niveaulinie hat im gedrehten Koordinatensystem

die Gleichung:

Es handelt sich also – wie behauptet – um eine Ellipse. ÿ

Wählt man speziell , so ergibt sich , also

Die Halbachsen haben die Längen , . Normierung der Eigenvektoren und Multiplikation mit diesen Werten ergibt die Scheitelpunkte im ursprünglichen Koordinatensystem.

Die Ellipse berührt den Graphen von von innen:

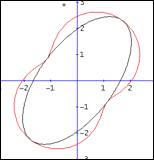
Abb. 8

Die Lage und die Maße ermöglichen es, eine Koordinatengleichung der Ellipse direkt aus derjenigen von durch eine Inversion am Kreis zu bestimmen.

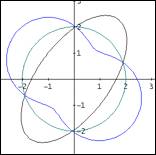
Abb. 9 Inversion am Kreis

Bei einer Inversion am Kreis muss das Produkt der Radien sein.

Aus folgt mit

dass

Ausmultplizieren ergibt eine Koordinatengleichung der Inversionskurve:

Also geht durch Inversion über in die Ellipse:

Benutzt man wieder Matrizen, lässt sich diese Ellipsengleichung sehr knapp mit der inversen Kovarianzmatrix schreiben:

Wegen ist sie äquivalent zu

Definition:

Sei W eine ebene Wolke aus Punkten, die nicht alle auf einer Geraden liegen.

sei die Kovarianzmatrix. Die Ellipsen mit der Gleichung

oder kurz

sowie ihre Translationen heißen Streuellipsen von W.

Die Ellipse mit heißt "Standardstreuellipse".

Aus der Annahme folgt und dass die Mindestpunktanzahl 3 beträgt.

Die Ellipsen sind also wohldefiniert. Der Grenzfall Kreis tritt genau dann auf, wenn . Die Streuellipsen sind die geometrischen Orte der Punkte, die denselben Mahalanobis-Abstand bzw. vom Zentrum mit Ortsvektor haben. Sie sind bei bivariater Normalverteilung die Konturlinien gleicher Wahrscheinlichkeitsdichte. Das Mahalanobis-Abstandsmaß geht den zu messenden Daten nicht voraus sondern entsteht gewissermaßen erst mit ihnen. Die (euklidische) Abstände werden entsprechend der Varianz in der jeweiligen Richtung gewichtet.

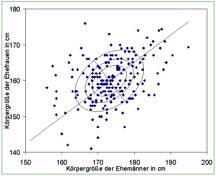
Abb. 10 Beispiel für Streuellipsen

Die eingezeichneten Geraden sind Translationen der Eigenräume der Kovarianzmatrix und Hauptachsen der Ellipsen. Man könnte sie als Dritte Regressionsgeraden bezeichnen. In diesem Beispiel wäre eine Verwendung der üblichen ersten oder zweiten Regressionsgerade wegen der Gleichartigkeit der dargestellten Daten ganz unangebracht, denn beide Komponenten des Datensatzes sind in gleicher Weise fehlerbehaftet. Die erste Regressionsgerade würde hier etwa 18° flacher, die zweite etwa 30° steiler verlaufen als die Hauptachse.

Steiner-Ellipsen als spezielle Streuellipsen

Satz: Die Punktwolke bestehe aus den Punkten mit.

Dann gilt:

Die Streuellipse ist die Steiner-Innenellipse des Dreiecks.

Die Streuellipse ist die Steiner-Umellipse des Dreiecks.

Beweis:

a) Berechnung der Streuellipse:

Für die Punktwolke ABC mit gilt:

Daher: , und

Die Streuellipsen sind also:

d.h.:

b) Berechnung der Steiner-Ellipse:

Jedes ebene Dreieck kann (zusammen mit seinen Steiner-Ellipsen) durch die umkehrbaren Abbildungen Verschiebung, Drehung, zentrische Streckung und Spiegelung auf ein geeignetes Dreieck mit abgebildet werden. Das Dreieck mit ist gleichseitig. Seine Steiner-Ellipsen sind daher bekannt: es handelt sich (aus Symmetriegründen) um den Innenkreis: und um den Umkreis: .

Wenn man das gleichseitige Dreieck durch die affine Abbildung mit

auf das Dreieck abbildet, geht sein Innenkreis in die Steiner-Innenellipse über. Denn eine affine Abbildung erhält Teilverhältnisse, und die Innenellipse berührt wie der Innenkreis die Dreiecksseiten in den Seitenmitten. Die Spaltenvektoren von M haben (als Bildvektoren der orthogonalen Kreisradien) konjugierte Richtung. Das legt zusammen mit dem Zentrum die Ellipse bereits fest. Sie sei durch die Koordinaten beschrieben.

Die Umkehrabbildung ist gegeben durch:

Durch Einsetzen in die Kreisgleichung erhält man:

Daraus folgt:

Die Steiner-Innenellipse hat die Gleichung:

Der Vergleich zeigt: Für ist die Streuellipse also die Steiner-Innenellipse.

Streckung mit dem Faktor 2 ergibt für die Umellipse. ÿ

Die Berechnung der Streuellipsen ist offenbar von der Anzahl der zugrunde liegenden Punkte unabhängig. Der Begriff der Steiner-Ellipse kann daher durch die im Satz genannte Charakterisierung allgemeiner gefasst werden.

Korollar: Zu jeder Punktwolke W gibt es Steiner-Ellipsen.

Der Extremaleigenschaft der Steiner-Ellipsen entspricht bei den Streuellipsen die Eigenschaft der "effektivsten Darstellung"².

Die Exzentrizität der Streuellipsen hängt vom Korrelationskoeffizienten und

vom Verhältnis der Varianzen ab:

Für ( also ) gilt:

Für gilt: für und für

Auch unkorrelierte Punktwolken haben also im Allgemeinen keine Kreise als Streuellipsen. Es gibt unkorrelierte Punktwolken mit Streuellipsen beliebiger Exzentrizität. Dieser Feststellung enthält eine Warnung vor zu großem Vertrauen in die Aussagekraft des optischen Eindrucks, den eine statistische Graphik erwecken kann. Falls möglich, sollte man V_x und V_ymit derselben Einheit darstellen.

Anwendung ergeben sich in Mustererkennung und Echtheitsprüfung von Geldscheinen³. Elliptische Galaxien bestehen aus Milliarden von Sternen. Mit bivariater Statistik kann jeder Streuellipsen der jeweilige Anteil an der Gesamtzahl der Sterne zugeordnet werden.

Abbildungsverzeichnis:

[Abb. 2] PISA-Konsortium (Hrsg.) PISA 2003. Der zweite Vergleich der Länder in Deutschland - Was wissen und können Jugendliche?, Münster, New York, München, Berlin: Waxmann 2005. S. 253.

(Schwarz-weiß-invertiert) Abdruck mit freundlicher Genehmigung des Verlags.

[Abb. 10] Daten aus: A Handbook of Small Data Sets.

Ed. by D.J. Hand et al.. London: Chapman and Hall 1994.

Literaturverzeichnis:

Koecher, Max: Lineare Algebra und Analytische Geometrie/Berlin;Heidelberg;

New York;Tokyo: Springer 1983. [ISBN 3-540-12572-8 ]

Tack, Thomas: Die dritte, vierte und fünfte Regressionsgerade.

MNU, Mathematischer und naturwissenschaftlicher Unterricht

59/1 (15.1.2006), S. 7-13. [ISSN 0025-5866.]

Internetquellen [Stand: jeweils 6. April 2007]:

¹ http://mathworld.wolfram.com/SteinerInellipse.html

² http://www.meteo.uni-bonn.de/mitarbeiter/PFried/multstat.pdf [S.15f]