Hans Walser, [20181008]

111111 durch 7

1 Einstiegsbeispiel

Es ist:

111111 : 7 = 15873 (1)

2 Verallgemeinerung

Es sei p eine Primzahl, p ≥ 7 und die Periodenlänge von im Dezimalsystem.

Dann ist die Dezimalzahl, die aus Einsen besteht, durch p teilbar.

3 Beispiele

p = 7. Es ist:

(2)

Daher ist die aus 6 Einsen bestehende Zahl 111111 durch 7 teilbar.

p = 11. Es ist:

(3)

Also ist 11 durch 11 teilbar.

p = 13. Es ist:

(4)

Kontrolle:

111111 : 13 = 8547 (5)

p = 17. Es ist:

(6)

Kontrolle:

1111111111111111 : 17 = 65359477124183 (7)

4 Beweis

Bei der Umwandlung eines Dezimalbruches in einen Bruch mit Zähler und Nenner wird der Dezimalbruch mit multipliziert und anschließend der Bruch subtrahiert. Damit fallen die unendlich vielen Stellen weg.

In unserem Fall heißt das:

(8)

Dabei ist n die aus den Ziffern der Periode von p bestehende Dezimalzahl.

Es ist also:

(9)

Nun ist nach der erweiterten dritten binomischen Formel:

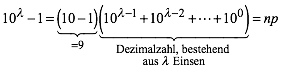(10)

Da 9 und p teilerfremd sind, teilt p die aus Einsen bestehende Zahl.

Umgekehrt ist 9 ein Teiler von n.

5 Folgerungen

Jede aus gleichen Ziffern bestehende Dezimalzahl ist durch p teilbar.

Beispiele:

222222 : 7 = 31746

333333 :7 = 47619 (11)

usw.

999999 : 7 =142857

Beim letzten Beispiel ergibt sich gemäß (9) die Zahl n.

Eine aus weniger als Neunen bestehende Dezimalzahl ist nicht durch p teilbar. Andernfalls könnte man mit dem entstehenden Quotienten einen periodischen Dezimalbruch für entwickeln der eine kleinere Periodenlänge als hat.

6 Weitere Teilbarkeiten

Gemäß (10) ist 9 ein Teiler von n.

Beispiel: für die zu p = 7 gehörende Zahl n = 142857 gilt:

142857 : 9 = 15873

142857 : 99 = 1443 (12)

142857 : 999 = 143

Hingegen ist:

(13)

Hintergrund: die Periodenlänge von p = 7 lässt sich zerlegen in . Das hat zur Folge, dass n auch teilbar ist durch Zusammensetzungen von 2 oder 3 Neunen.

Beweis: Sei . Damit ist:

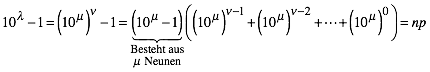(14)

Der aus Neunen bestehende Faktor ist wegen nicht durch p teilbar. Daher ist er ein Teiler von n.