Hans Walser, [20120121]
120¡-Dreieck
1 FlŠchensatz
Wir beginnen mit einem
120¡-Dreieck (wei§, im Zentrum) und ergŠnzen gemŠ§ Abbildung 1.
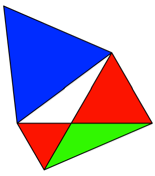
Abb. 1: Blau = Rot +
GrŸn
Es gilt der
FlŠchensatz:
Blau = Rot + GrŸn
Das grŸne Dreieck ist
kongruent zum wei§en Startdreieck.
2
Beweise des FlŠchensatzes
2.1
Kosinussatz
FŸr das gleichseitige
blaue Dreieck haben wir den FlŠcheninhalt 
. FŸr die gleichseitigen roten Dreiecke haben wir die
FlŠcheninhalte 
und 
. Das grŸne Dreieck hat den FlŠcheninhalt 
.
Andererseits gilt im
wei§en Dreieck nach dem Kosinussatz:
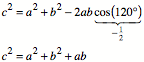
Beidseitige
Multiplikation mit 
liefert die
Aussage des FlŠchensatzes.
2.2
Pythagoras
Durch geeignete
Zerlegungen kšnnen wir die Pythagoras-Situation mit aufgesetzten gleichseitigen
Dreiecken (statt Quadraten) erreichen. Dies geht auf zwei Arten.
2.2.1
Erste Zerlegung
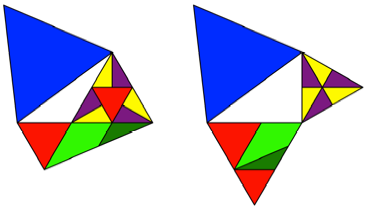
Abb. 2: Erste Zerlegung
2.2.2
Zweite Zerlegung
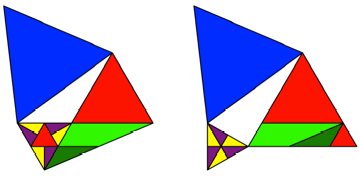
Abb. 3: Zweite Zerlegung
Literatur
[Walser 2010] Walser,
Hans: Ein FlŠchensatz. In: Katja KrŸger und Philipp Ullmann (Hg.): Von
Geometrie und Geschichte in der Mathematikdidaktik. Festschrift zum 65.
Geburtstag von Lutz FŸhrer. EichstŠtt: Polygon-Verlag 2010. ISNB:
978-3-928671-60-6. S. 41-52.