Hans Walser, [20170420]
Anregungen: E. V., M. und Y. W., M.
18-Eck
1 Problemstellung
Es ist zu zeigen, dass in der Figur (Abb. 1) mit den gegebenen Winkeln die beiden fett eingezeichneten Strecken gleich lang sind.
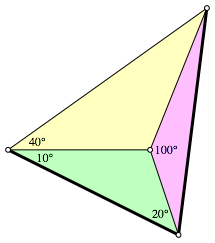
Abb. 1: Basisfigur
2
Forbidden
fruit taste the sweetest
Die in der Problemstellung vorkommenden Winkel sind alle nicht mit Zirkel und Lineal konstruierbar. Wir kšnnen das Problem also nicht empirisch mit Zirkel und Lineal angehen.
Diese Winkel erscheinen aber alle im regelmŠ§igen 18-Eck mit seinen Diagonalen.
3 Ein ăbesondererŇ Punkt im regelmŠ§igen 18-Eck
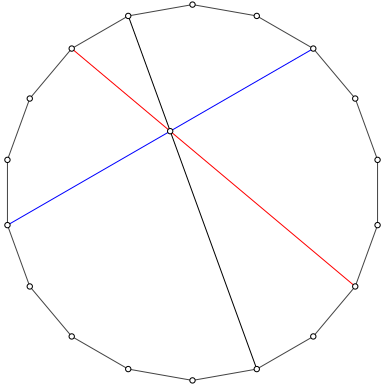
Abb. 2: Schnittpunkt dreier Diagonalen
Im regelmŠ§igen 18-Eck (Abb. 2) verlaufen die drei eingezeichneten Diagonalen durch einen gemeinsamen Punkt. Siehe auch (Walser 2012, S. 31).
Die schwarze Diagonale ist eine Mittelpunktdiagonale.
Fźr den Beweis der Schnittpunkteigenschaft lokalisieren wir den Schnittpunkt der schwarzen mit der roten Diagonalen (schwarz-roter Schnittpunkt) und den Schnittpunkt der schwarzen mit der blauen Diagonalen (schwarz-blauer Schnittpunkt) je relativ zum Mittelpunkt des 18-Eckes.
3.1 Schwarz-roter Schnittpunkt
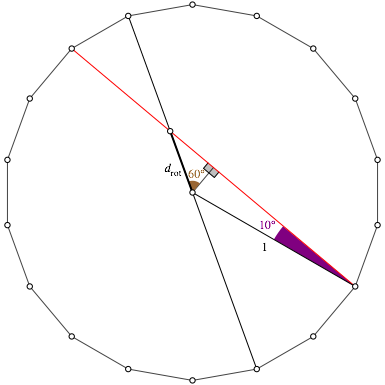
Abb. 3: Schwarz-roter Schnittpunkt
Den Umkreisradius des regelmŠ§igen 18-Ecks setzen wir 1. Die in der Abbildung 3 eingezeichneten Winkel lassen sich leicht mit KreiswinkelsŠtzen herleiten.
Fźr den Abstand drot des schwarz-roten Schnittpunktes vom Mittelpunkt des regelmŠ§igen 18-Eckes erhalten wir:
![]() (1)
(1)
3.2 Schwarz-blauer Schnittpunkt
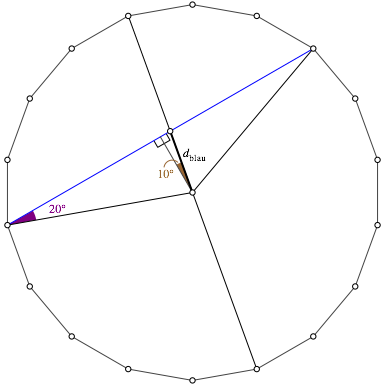
Abb. 4: Schwarz-blauer Schnittpunkt
Die in der Abbildung 4 eingezeichneten Winkel lassen sich leicht mit KreiswinkelsŠtzen herleiten. Fźr den Abstand dblau des schwarz-blauen Schnittpunktes vom Mittelpunkt des regelmŠ§igen 18-Eckes erhalten wir:
![]() (2)
(2)
Fźr die Schnittpunkteigenschaft der drei Diagonalen haben wir zu zeigen:
![]() (3)
(3)
Fźr die linke Seite erhalten wir mit dem Additionstheorem des Sinus:
![]() (4)
(4)
Fźr die rechte Seite erhalten wir:
![]() (5)
(5)
Damit ist die Schnittpunkteigenschaft der drei Diagonalen bewiesen.
4 Einbetten ins regelmŠ§ige 18-Eck
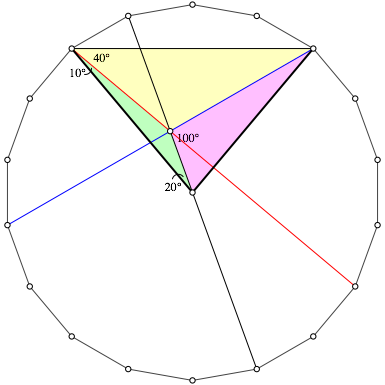
Abb. 5: Einbettung ins regelmŠ§ige 18-Eck
Nun geht es ratzfatz.
Wir betten die Figur der Problemstellung (Abb. 1) ins regelmŠ§ige 18-Eck ein (Abb. 5) und verifizieren die Winkel.
Die beiden schwarzen Strecken sind je der Umkreisradius, also gleich lang. Dies war zu zeigen.
5 Varianten
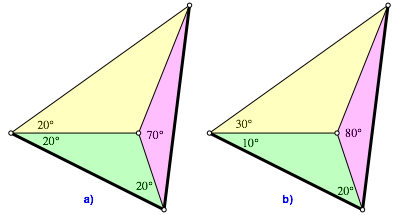
Abb. 6: Varianten
Die Abbildung 6 zeigt zwei Varianten der Problemstellung.
Literatur
Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0.