Hans Walser, [201610113]

2-reguläre Dreiecksfiguren

1 Worum geht es?

Figuren mit kongruenten gleichseitigen Dreiecken, so dass an jeder Ecke genau 2 Dreiecke zusammenkommen.

2 Parkette und Flächenornamente

Das einfachste unendlich große Beispiel ist das aus Dreiecken und Sechsecken bestehende Parkett der Abbildung 1.

Abb. 1: Parkett

Die Abbildung 2 zeigt eine Variante.

Abb. 2: Variante

Die Abbildung 3 zeigt ein Beispiel, in welchem auch der rechte Winkel vorkommt.

Abb. 3: Beispiel mit rechten Winkeln

Die Abbildung 4 zeigt indessen ein falsches Beispiel. Das Parkett ist 3-regulär. An jeder Ecke kommen drei Dreiecke zusammen.

Abb. 4: Falsches Beispiel

Bei gelenkigen Verbindungen an den Ecken ist die Figur der Abbildung 1 nicht starr. Die Abbildung 5 zeigt eine Folge von bewegten Parketten.

Abb. 5: Bewegung

3 Sierpiński-Unterteilung

Wir können jedes Dreieck flächenmäßig durch die Mittelparallelen vierteln und das mittlere Viertel herausnehmen (Abb. 6). Bei diesem Prozess bleibt die 2-Regularität erhalten. Die Anzahl der Dreiecke verdreifacht sich.

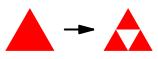
Abb. 6: Sierpiński-Unterteilung

Die Abbildung 7 zeigt das Parkett der Abbildung 1 nach dem ersten Sierpiński-Unterteilungsschritt.

Abb. 7: Erster Schritt der Sierpiński-Unterteilung

Die Abbildung 8 zeigt die Situation nach dem zweiten Sierpiński-Unterteilungsschritt.

Abb. 8: Zweiter Schritt der Sierpiński-Unterteilung

Und so weiter und so fort.

Bei den Flächenornamenten gibt es 17 Symmetrieklassen (Walser 2014, S. 83f). Zu jeder Symmetrieklasse gibt es (mindestens) ein Beispiel mit 2-regulären Dreiecken [1].

Man beachte aber, dass die Unterteilung in der Abbildung 9 falsch ist. Es ist keine Sierpiński-Unterteilung. Wir haben nun Ecken, an denen drei Dreiecke zusammenkommen. Dies steht im Widerspruch zur 2-Regularität.

Abb. 9: Falsche Unterteilung, nicht 2-regulär

4 Bandornamente

Die Abbildung 10 zeigt ein recht einfaches Bandornament. Im rechten Teil der Abbildung sind zusätzlich die Symmetrieachsen und Symmetriezentren eigezeichnet. Das Bandornament gehört zur Symmetrieklasse F₅ (Bezeichnung nach (Walser 2014, S. 80, 81).

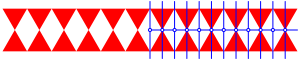
Abb. 10: Bandornament, Symmetrieklasse F₅

Das Bandornament der Abbildung 11 gehört ebenfalls zur Symmetrieklasse F₅. Es ist sozusagen die verwackelte Version des Beispiels der Abbildung 7 und hat daher eine kleinere Symmetrieachsendichte.

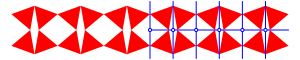
Abb. 11: F₅

Die drei Beispiele der Abbildung 12 gehören alle zur Symmetrieklasse F₆.

Abb. 12: F₆

Das Beispiel der Abbildung 13 gehört zur Symmetrieklasse F₂.

Abb. 13: F₂

Zu jeder Symmetrieklasse der Bandornamente gibt es ein Beispiel aus 2-regulären Dreiecken [2].

Mit Ausschnitten von Bandornamenten können weitere Parkette gebaut werden (Abb. 14 und 15)

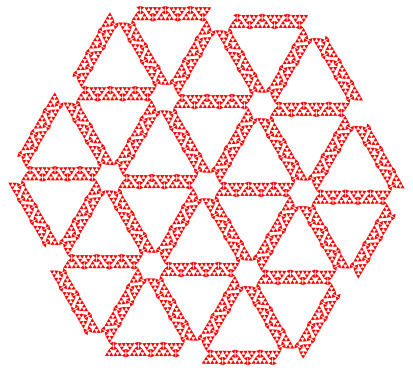
Abb. 14: Parkett

Abb. 15: Parkett

5 Figuren abschließen

Die bisherigen Beispiele gingen alle ins Unendliche und brauchen daher unendlich viele Dreiecke. Es gibt aber auch endliche 2-reguläre Dreiecksfiguren.

Zunächst können wir jedes offene Parkett oder Bandornament mit einer der Figuren der Abbildung 16 abschließen.

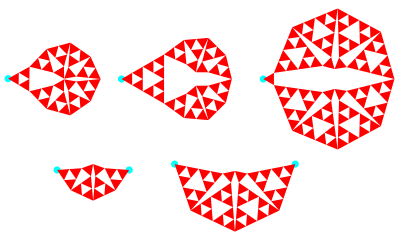
Abb. 16: Schlussfiguren

Das vierte Beispiel sieht falsch aus, man meint, im innersten Punkt kämen vier Dreiecke zusammen. Die Figur ist aber korrekt, es sind zwei verschiedene Punkte. Bezogen auf die Seitenlänge 1 der Dreiecke haben die beiden Punkte den Abstand 0.0548.

Die Abbildungen 17 und 18 zeigen abgeschlossene Figuren, welche aus den Figuren der Abbildungen 14 und 15 entstanden sind. Sie enthalten nur endlich viele Dreiecke.

Abb. 17: Abgeschlossene Figur

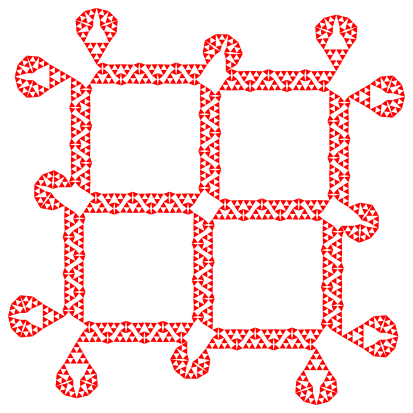
Abb. 18: Abgeschlossene Figur

6 Weitere endliche 2-reguläre Dreiecksfiguren

Im Folgenden einige Beispiele von einfacheren 2-regulären Dreiecksfiguren, geordnet nach Symmetrien.

Abb. 19: Symmetrien des Rechteckes

Abb. 20: Symmetrien des Rechtecks

Die Abbildung 21 zeigt drei Beispiele mit den Symmetrien des gleichseitigen Dreiecks. Das kleinste Beispiel enthält 42 kleine gleichseitige Dreiecke. Ich kenne keine endliche 2-reguläre Dreiecksfigur mit weniger gleichseitigen Dreiecken.

Abb. 21: Symmetrien des gleichseitigen Dreiecks

Die Abbildung 22 zeigt zwei Beispiele mit den Symmetrien des Quadrates. Sie enthalten 56 und 80 kleine Dreiecke.

Abb. 22: Symmetrien des Quadrates

Die Abbildungen 23 und 24 zeigen Beispiele mit den Symmetrien des regelmäßigen Fünfeckes und Sechseckes.

Abb. 23: Symmetrien des regelmäßigen Fünfeckes

Abb. 24: Symmetrien des regelmäßigen Sechseckes

Die Figur der Abbildung 25 hat dieselben Symmetrien wie das regelmäßige Siebeneck. Die Figur enthält 56 Dreiecke.

Abb. 25: 56 Dreiecke. Siebenteilige Symmetrie

Nun ist es ja so, dass das regelmäßige Siebeneck nicht mit Zirkel und Lineal oder einer entsprechenden dynamischen Geometrie-Software gezeichnet werden kann. Es gibt aber andere Methoden zur Konstruktion eines regelmäßigen Siebenecks.

Die Abbildung 26 zeigt ein Gelenkmodell mit 168 Stäben gleicher Länge. In geschlossenem Zustand entspricht es der Figur der Abbildung 25.

Abb. 26: Gelenkmodell

Wenn wir im Gelenkmodell der Abbildung 26 einen Doppelsektor mehr einbauen und das Gelenk vor dem Schließen etwas auffalten, erhalten wir eine 2-reguläre Dreiecksfigur mit den Symmetrien des regelmäßigen Achtecks (Abb. 27).

Abb. 27: Achtteilige Symmetrie

Leider lassen sich weitere 2-reguläre Dreiecksfiguren nicht mehr mit diesem mechanischen Modell realisieren, weil es zu Selbstüberlappungen kommt.

Die Abbildung 28 zeigt falsche Figuren. Sie sehen beinahe aus wie die Abbildungen 25 bis 27. Die Figuren haben die Symmetrien des regelmäßigen Elfecks, Zwölfecks und 13-Ecks. Leider sind sie nicht 2-regulär. Wir haben Dreiecksecken, an denen drei Dreiecke statt nur zwei zusammenkommen. Nichtsdestotrotz kann natürlich ein entsprechendes Gelenkmodell zur Konstruktion dieser Figuren gebaut werden. Schön sind sie allemal.

Das regelmäßige Elfeck und 13-Eck lassen sich nicht mit Zirkel und Lineal konstruieren.

Abb. 28: Falsche Figuren, nicht 2-regulär.

Literatur

Walser, Hans (2014): Symmetrie in Raum und Zeit. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-46-2.

Websites

[1] Hans Walser: Flächenornamente (21.10.2016):

www.walser-h-m.ch/hans/Miniaturen/F/Flaechenornamente/Flaechenornamente.htm

[2] Hans Walser: Bandornamente (21.10.2016):

http://www.walser-h-m.ch/hans/Miniaturen/B/Bandornamente/Bandornamente.htm