Hans Walser, [20130727a]

Dreieck und Sechseck

Anregung: H. K. S., L.

1 Worum geht es?

Die Abbildung 1 zeigt eine gemeinsame Zerlegung eines Dreieckes und eines dazu flächengleichen Sechseckes.

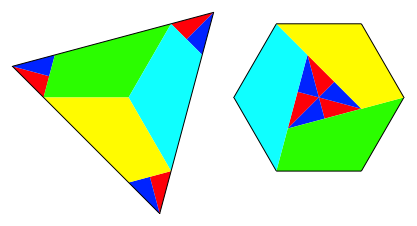
Abb. 1: Zerlegungsgleiche Figuren

Wie finden wir die Puzzle-Teile?

2 Flächengleiche Figuren

Auf dem Einheitskreis zeichnen wir zwölf Punkte in gleichen Abständen, also die Eckpunkte des regelmäßigen Zwölfecks, und dazu das rote Dreieck und das blaue Sechseck gemäß Abbildung 2.

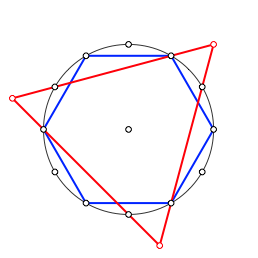
Abb. 2: Im Zwölfeck

Das rote Dreieck hat den Inkreisradius und daher den Flächeninhalt . Das blaue Sechseck hat den Umkreisradius 1 und daher den Flächeninhalt . Die beiden Figuren sind also flächengleich.

3 Konstruktion der Zerlegung

Die Abbildung 3 zeigt nun das Puzzle-Teil, das zum Schlüssel der gemeinsamen Zerlegung wird. Es ist ein Ausschnitt aus dem regelmäßigen Zwölfeck.

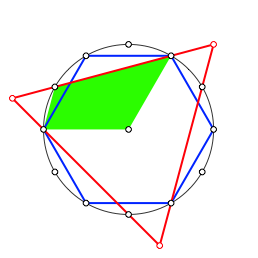
Abb. 3: Puzzle-Teil

Mit drei solcher Puzzle-Teile, jeweils um 120° verdreht, können wir das rote Dreieck bis auf drei kleine Dreiecke an den Ecken ausfüllen (Abb. 4).

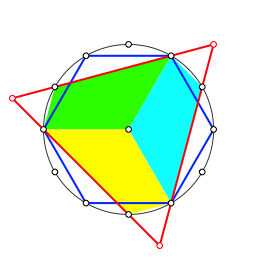
Abb. 4: Puzzle-Teile im Dreieck

Andererseits können wir mit denselben drei Puzzle-Teilen das blaue Sechseck so belegen, dass in der Mitte ein Dreieck übrig bleibt (Abb. 5).

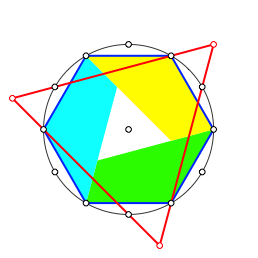
Abb. 5: Puzzle-Teile im Sechseck

Bleibt noch das Restproblem, das dreieckige Loch im Zentrum des blauen Sechseckes auf die drei kleinen Dreiecke an den Ecken des roten Dreiecks zu verteilen. Wir müssen also ein Dreieck dritteln. Die Abbildung 6 zeigt, wie das geht.

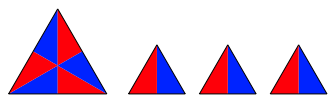
Abb. 6: Drittelung des Dreiecks

Damit erhalten wir die gemeinsame Zerlegung der Abbildung 1.