Hans Walser, [20170530]
3d-Puzzle
1 Erinnerung: 2d-Puzzle
Die Abbildung 1 zeigt ein Puzzle in der Ebene (Hemme 1989). Die Figur kann in 4 kongruente und zur Ausgangsfigur Šhnliche Figuren zerlegt werden. Die Figur besteht aus einem Dreiviertelquadrat.
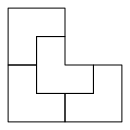
Abb. 1: Puzzle in der Ebene
2 †bertragung in den Raum
Wir arbeiten mit einem Siebenachtelwźrfel, der in 8 kongruente und zur Ausgangsfigur Šhnliche Figuren zerlegt werden kann.
Die Idee ist naheliegend, ich brauchte aber die Zeichnungen und den schrittweisen Zusammenbau, um mir klar zu machen, dass es wirklich funktioniert.
Die
Abbildung 2 zeigt die acht Teile in einer Sprengzeichnung. Sie sind bereits in
der fźr den Zusammenbau erforderlichen Anordnung.
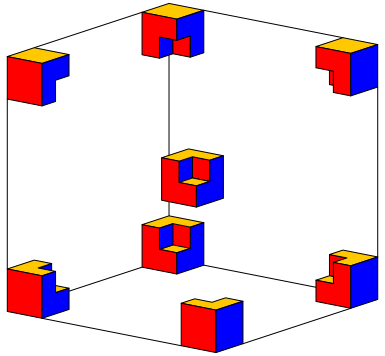
Abb. 2: Die acht Teile
Die Abbildungen 3 bis 6 zeigen den Zusammenbau.
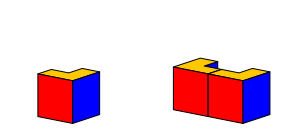
Abb. 3: Die beiden ersten Teile
In den nŠchsten Schritten kšnnen wir die Basis fertigstellen (Abb. 5).
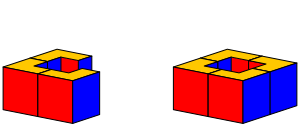
Abb. 4: Die Basis ist fertig
Nun kšnnen wir das Mittelstźck einsenken und mit dem Bau der zweiten Etage beginnen (Abb. 5).
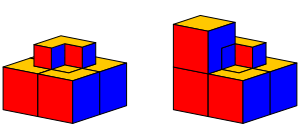
Abb. 5: Mittelstźck und Beginn der zweiten Etage
Anschlie§end kann der Zusammenbau fertiggestellt werden (Abb. 6).
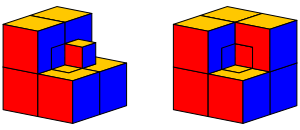
Abb. 6: Fertiggestelltes Puzzle
[1] gibt eine andere †bertragung der Puzzle-Idee in den Raum.
Literatur
Hemme, Heinrich (1989): Geometrische Gerźchte: Figuren, die sich selbst vervielfachen. bild der wissenschaft, 5-1989. 141-144.
Websites
[1] Hans Walser: Viererpuzzle im Raum (31.05.2017):
www.walser-h-m.ch/hans/Miniaturen/V/Viererpuzzle_im_Raum/Viererpuzzle_im_Raum.htm