Hans Walser, [20230403]

3d-Schachbrett

Idee und Anregung: Stephan Rosebrock, Karlsruhe

1 Worum geht es?

Farbspiele im Raster. Approximation von Kugel und Oktaeder. Oberflächenmuster. Parität gerade / ungerade.

2 Erinnerung: 2d-Schachbrett

Die Abbildung 1 zeigt das übliche zweidimensionale Schachbrett. Zwei Felder mit gemeinsamer Seite sind ungleich gefärbt. Zwei Felder mit gemeinsamer Ecke haben gleiche Farbe. Ein Läufer kann also entweder nur rote oder nur grüne Felder erreichen.

Abb. 1: Zweidimensionales Schachbrett

Wir verschärfen nun die Färbungsbedingung: Zwei Felder, die eine Seite oder eine Ecke gemeinsam haben, sind ungleich gefärbt. Für die Minimallösung brauchen wir vier Farben (Abb. 2). Ein Läufer kann entweder nur gelbe und rote Felder erreichen oder nur grüne und blaue.

Abb. 2: Vier Farben

3 Im Raum

Es handelt sich beim 3d-Schachbrett natürlich nicht um ein „Brett“, sondern um einen Würfelhaufen.

Wir können sukzessiv verschärfte Färbungsbedingungen stellen:

(1) Zwei Würfel mit gemeinsamer Seitenfläche sollen ungleich gefärbt sein. Wir kommen in diesem Fall mit zwei Farben aus.

(2) Zwei Würfel mit gemeinsamer Seitenfläche sowie zwei Würfel mit gemeinsamer Kante sollen ungleich gefärbt sein. Wir benötigen nun vier Farben.

(3) Zwei Würfel mit gemeinsamer Seitenfläche sowie zwei Würfel mit gemeinsamer Kante sowie zwei Würfel mit gemeinsamer Ecke sollen ungleich gefärbt sein. Wir brauchen acht Farben.

3.1 Zwei Farben

3.1.1 Raster

Zwei Würfel mit gemeinsamer Seitenfläche sollen ungleich gefärbt sein (Abb. 3). Für die Minimallösung brauchen wir zwei Farben. Zwei Würfel mit gemeinsamer Kante sind gleich gefärbt. Zwei Würfel mit gemeinsamer Ecke sind ungleich gefärbt.

Abb. 3: Zwei Farben

Die Abbildung 4 zeigt den systematischen Aufbau eines 4×4×4-Rasters mit zwei Farben.

Abb. 4: Systematischer Aufbau

3.1.2 Kugelapproximation

Die Abbildungen 5 und 6 zeigen die Approximation einer Kugel mit dem Durchmesser 32 im Raster mit zwei Farben. Beim Spiegeln an der Äquatorebene werden die Farben vertauscht.

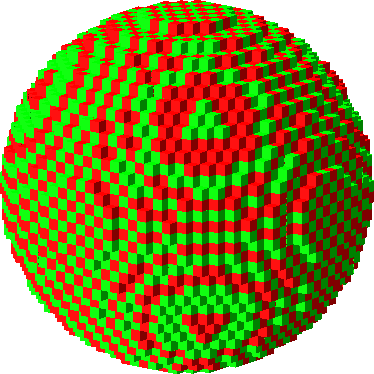
Abb. 5: Kugelapproximation

Abb. 6: Kugel und Approximation

Die Abbildungen 7 und 8 zeigen dasselbe für eine Kugel mit dem ungeraden Durchmesser 31. Beim Spiegeln an der Äquatorebene bleiben die Farben erhalten.

Abb. 7: Ungerader Durchmesser

Abb. 8: Kugel mit ungeradem Durchmesser

3.1.3 Oktaeder

Die Abbildungen 9 und 10 zeigen je eine Oktaederapproximation mit geradem beziehungsweise ungeradem Durchmesser. Beim geraden Durchmesser ist die Oberfläche zweifarbig.

Abb. 9: Oktaeder mit geradem Durchmesser

Bei ungeradem Durchmesser ist die Oberfläche monochrom.

Abb. 10: Oktaeder mit ungeradem Durchmesser

3.2 Vier Farben

3.2.1 Raster

Zwei Würfel mit gemeinsamer Seitenfläche sowie zwei Würfel mit gemeinsamer Kante sollen ungleich gefärbt sein (Abb. 11). Wir benötigen nun vier Farben. Übereck liegende Würfel haben dieselbe Farbe.

Abb. 11: Vier Farben

Die Abbildung 12 zeigt den systematischen Aufbau eines 4×4×4-Rasters mit vier Farben.

Abb. 12. Systematischer Aufbau

Die Abbildung 13 zeigt die Anordnung der roten Würfel.

Abb. 13: Die roten Würfel

3.2.2 Kugelapproximationen

Die Abbildungen 14 und 15 zeigen Kugelapproximationen mit geradem beziehungsweise ungeradem Durchmesser.

Abb. 14: Gerader Durchmesser

Abb. 15: Ungerader Durchmesser

3.2.3 Oktaeder

Die Abbildungen 16 und 17 zeigen Oktaeder mit geradem beziehungsweise ungeradem Durchmesser.

Abb. 16: Gerader Durchmesser

Abb. 17: Ungerader Durchmesser

3.3 Acht Farben

3.3.1 Raster

Zwei Würfel mit gemeinsamer Seitenfläche sowie zwei Würfel mit gemeinsamer Kante sowie zwei Würfel mit gemeinsamer Ecke sollen ungleich gefärbt sein (Abb. 18). Wir brauchen acht Farben. Welches ist die achte Farbe?

Abb. 18: Acht Farben

Die Abbildung 19 zeigt den systematischen Aufbau. Jetzt sehen wir auch die achte Farbe: schwarz.

Abb. 19: Aufbau

Die Abbildung 20 zeigt die Anordnung der roten Würfel.

Abb. 20: Anordnung der roten Würfel

3.3.2 Kugelapproximationen

Die Abbildungen 21 und 22 zeigen Kugelapproximationen mit geradem beziehungsweise ungeradem Durchmesser.

Abb. 21: Gerader Durchmesser

Abb. 22: Ungerader Durchmesser

3.3.3 Oktaeder

Die Abbildungen 23 und 24 zeigen Oktaeder mit geradem beziehungsweise ungeradem Durchmesser.

Abb. 23: Gerader Durchmesser

Abb. 24: Ungerader Durchmesser