Hans Walser, [20231021]
512
Idee und Anregung: Swetlana Nordheimer, Berlin
1 Worum geht es?
Es ist 83 = 512.
Abzählproblem. Kombinatorische und Räumliche Lösung. Erkennen von geometrischen Mustern und Zahlenmustern.
2 Die Spirale
Wie viele Quadrate enthält die Spirale (Abb. 1).
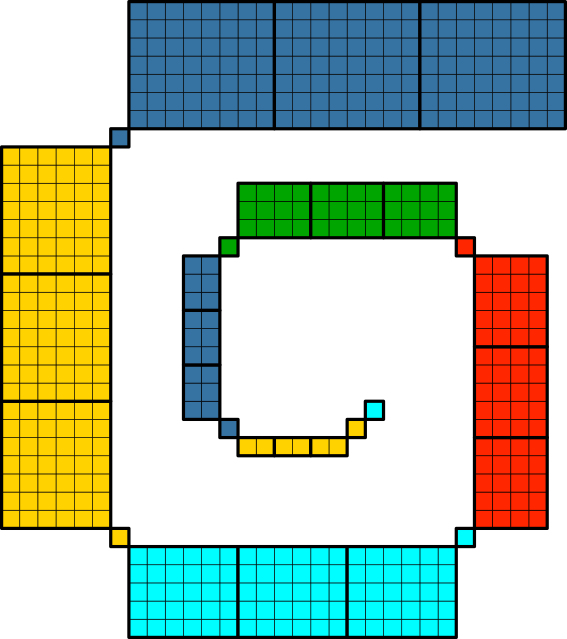
Abb. 1: Spirale
3 Abzählen mit Pfiff und Pascal
3.1 Zahlen im Pascal-Dreieck
Das äußerste, erste, blaue, Teilstück besteht aus drei Rechtecken mit den Seitenlängen 8 und 7 sowie einem Einzelquadrat. Es enthält also 3•8•7 + 1 = 3•56 + 1 Quadrate.
Das zweite, gelbe, Teilstück besteht aus drei Rechtecken mit den Seitenlängen 7 und 6 sowie einem Einzelquadrat. Es hat also 3•7•6 + 1 = 3•42 + 1 Quadrate.
Das dritte, hellblaue, Teilstück besteht aus drei Rechtecken mit den Seitenlängen 6 und 5 sowie einem Einzelquadrat. Es hat also 3•6•5 + 1 = 3•30 + 1 Quadrate.
Wir erkennen das Muster. Jedes Teilstück besteht aus drei Rechtecken mit den Seitenlängen n und n – 1 sowie einem Einzelquadrat. Dabei geht n von 8 hinunter bis 1.
Für die Gesamtsumme S erhalten wir somit:
S = 3•(56 + 42 + 30 + 20 + 12 + 6 + 2 + 0) + 8•1
Aus der Klammer können wir den Faktor 2 ausklammern:
S = 6•(28 + 21 + 15 + 10 + 6 + 3 + 1 + 0) + 8•1
Die Zahlen in der Klammer kennen wir aber. Sie erscheinen auch in einer Schrägzeile im Pascal-Dreieck der Binomialkoeffizienten (gelb markiert in Abb. 2).
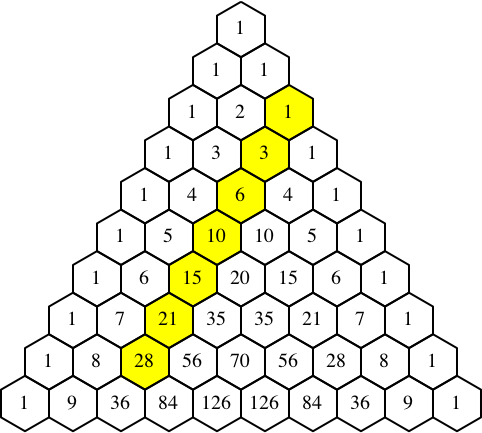
Abb. 2: Zahlen im Pascal-Dreieck
3.2 Das Weihnachts-Socke-Theorem
Die Summe der gelb markierten Zahlen im Pascal-Dreieck ist die rot markierte Zahl 84, rechts unten im Anschluss an die gelb markierten Zahlen (Abb. 3).
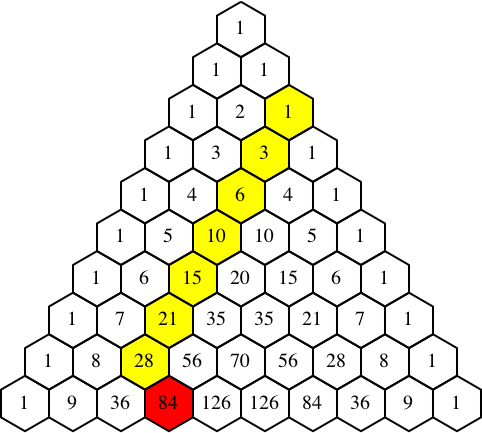
Abb. 3: Summe
3.3 Weitere Beispiele
Bevor wir dies beweisen, einige weitere Beispiele (Abb. 4).
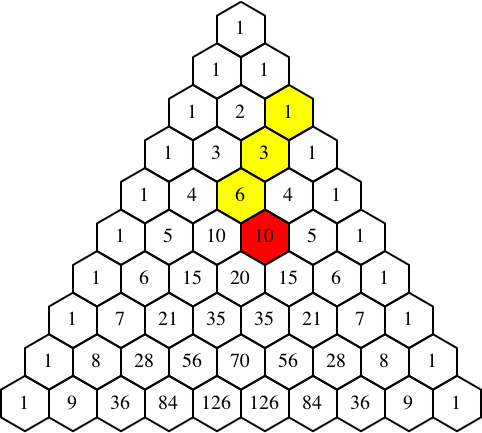
Abb. 4.1: Beispiel
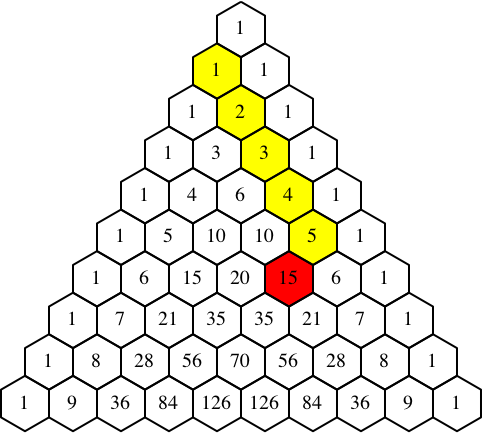
Abb. 4.2: Beispiel
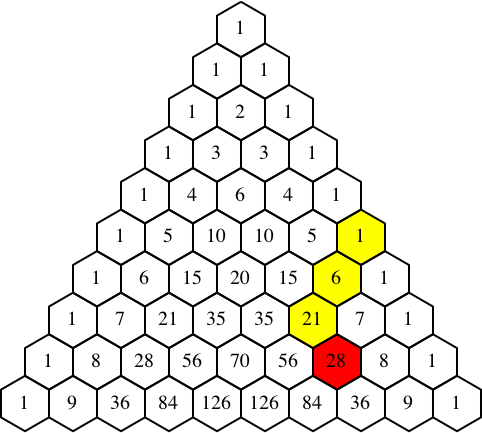
Abb. 4.3: Beispiel
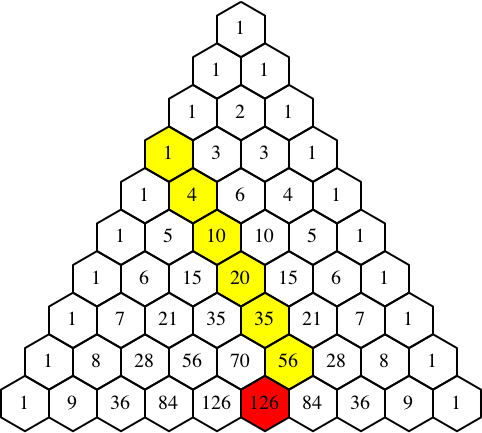
Abb. 4.4: Beispiel
Die Figuren erinnern an die vom Weihnachtsmann gebrachten, mit Zahlen gefüllten Socken. Die Summe der Zahlen im Schaft ist gleich groß wie die Zahl in der Fußspitze. Formal:
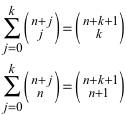
3.4 Beweis
Für den Beweis verwenden wir die Rekursionsformel für die Binomialkoeffizienten (Abb. 5):
![]()
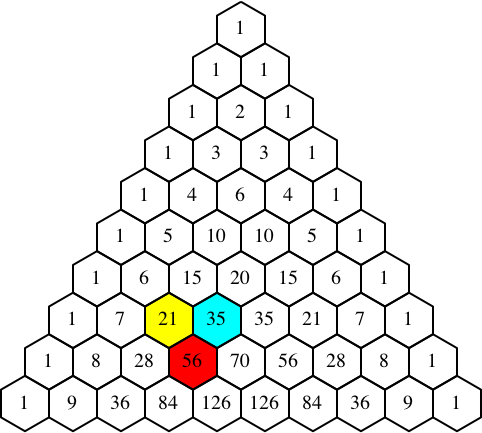
Abb. 5: Rot = Gelb + Cyan
Die Abbildung 6 illustriert nun den Rekursionsbeweis für das Weihnachts-Socke-Theorem.
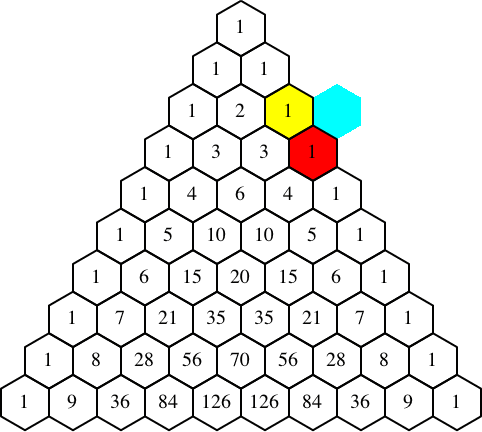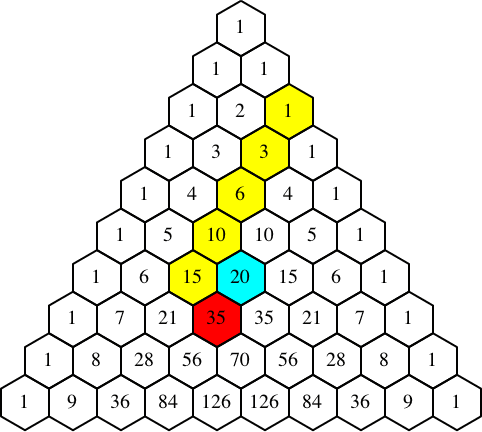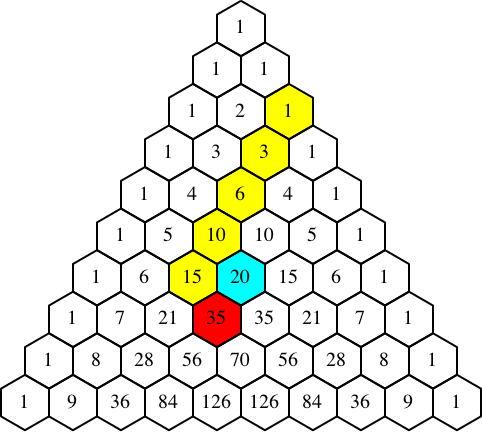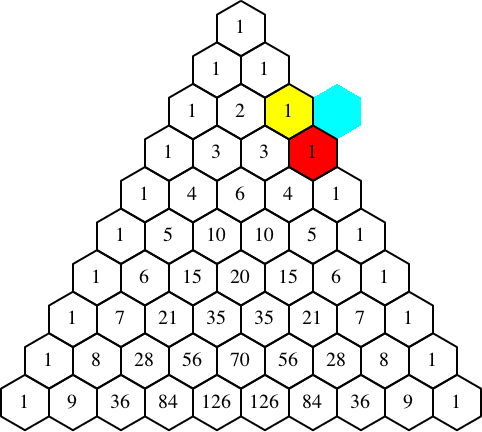
Abb. 6: Weihnachts-Socke-Theorem
3.5 Anzahl Quadrate
Nun zurück zu unserem Abzählproblem.
Für die Summe S der Anzahl der Quadrate in der Spirale (Abb. 1) erhalten wir:
S = 6•(28 + 21 + 15 + 10 + 6 + 3 + 1 + 0) + 8•1 = 6•84 + 8 = 504 + 8 = 512
4 Abzählen im Raum
4.1 Von Quadraten zu Würfeln
Wir ersetzen die Quadrate durch Würfel (Abb. 7).
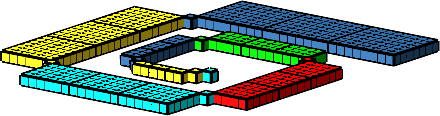
Abb. 7: Situation im Raum
Die Abbildung 8 zeigt den Übergang von der ebenen Situation der Abbildung 1 zur räumlichen Situation der Abbildung 7.
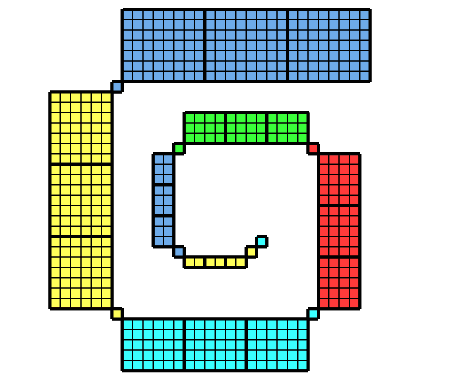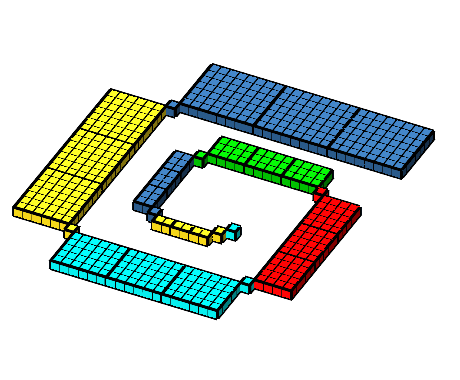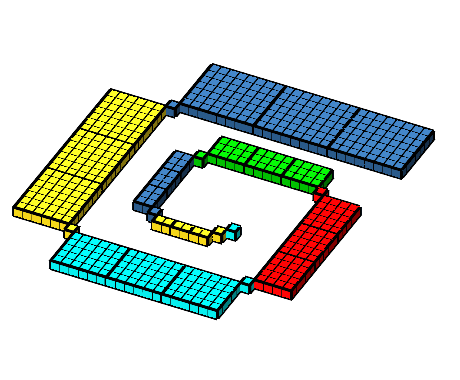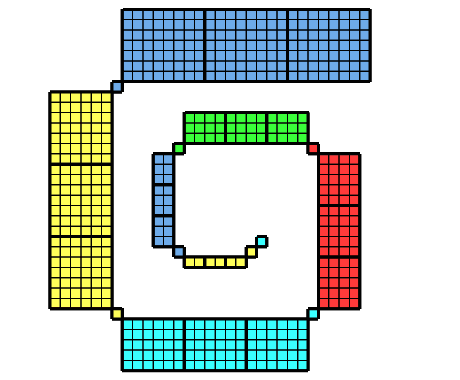
Abb. 8: Von der Ebene in den Raum
4.2 Andere Anordnung im Raum
Die Abbildung 9 zeigt das erste, blaue Teilstück der Figur der Abbildung 7. Es besteht aus drei rechteckigen Platten mit den Seitenlängen 8 und 7 und der Dicke 1 sowie einem Einzelwürfel.
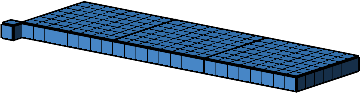
Abb. 9: Erster Anteil
Diese vier Teilfiguren ordnen wir nun anders an (Abb. 10).
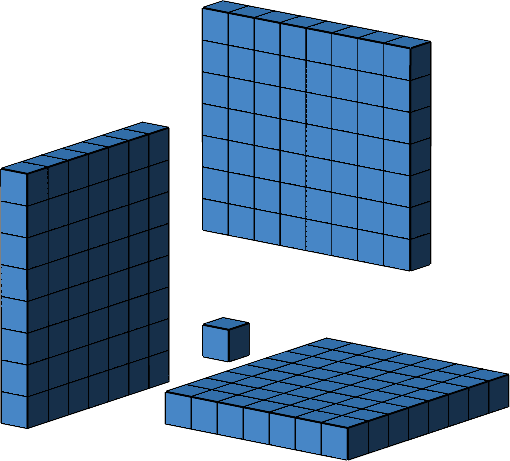
Abb. 10: Andere Anordnung im Raum
Wir können nun die drei rechteckigen Platten simultan zusammenschieben, bis sie den Einzelwürfel berühren (Abb. 11).
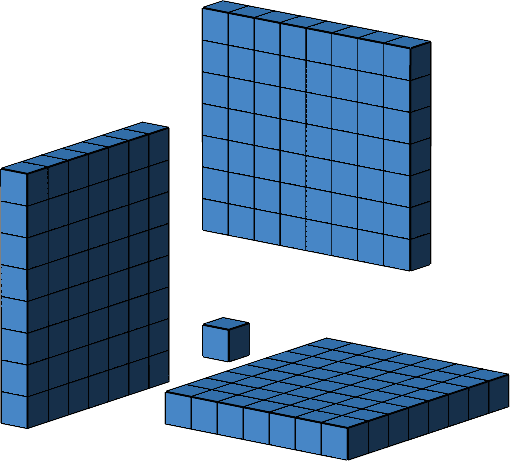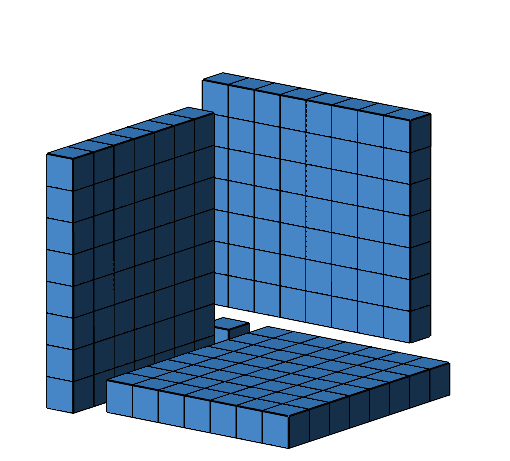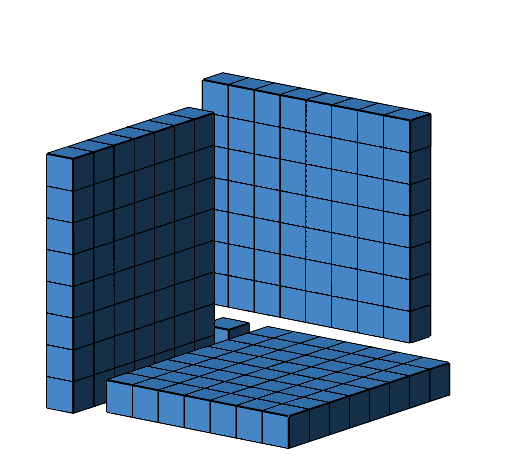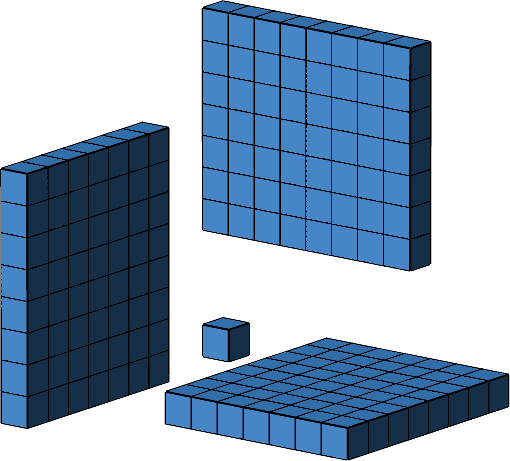
Abb. 11: Zusammenschieben der Platten
Als Endlage entsteht eine räumliche Ecke (Abb. 12).
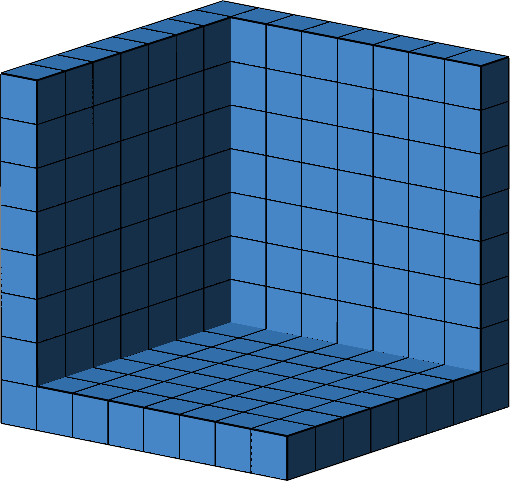
Abb. 12: Ecke
Analog können wir mit den weiteren Teilstücken verfahren. Die Abbildung 13 zeigt ein Beispiel.
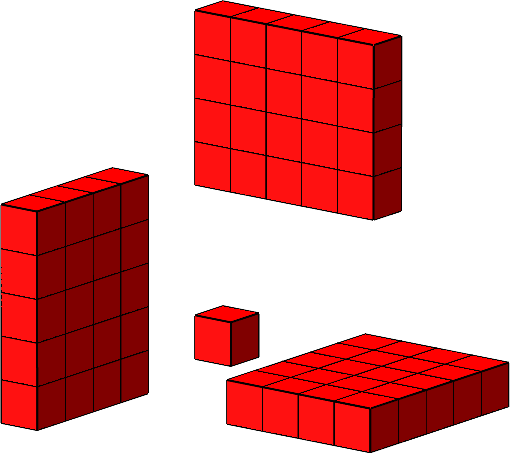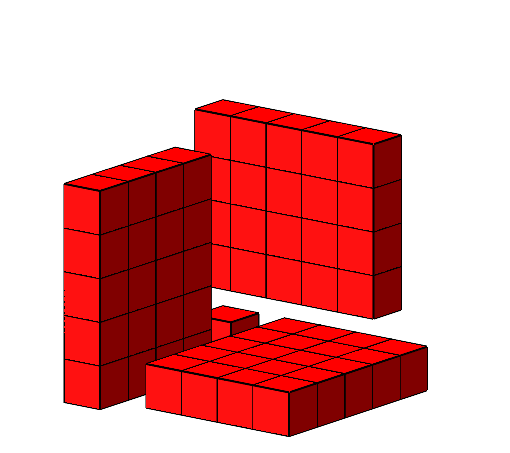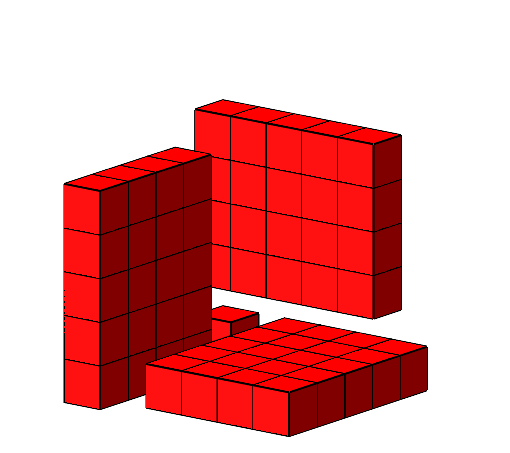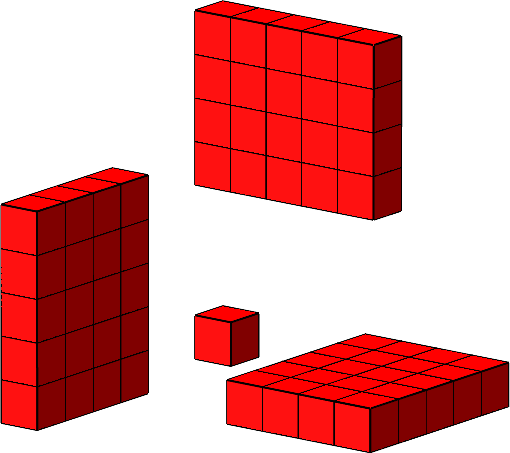
Abb. 13: Weiteres Beispiel.
4.3 Ein großer Würfel entsteht
Die entstehenden räumlichen Ecken lassen sich ineinanderlegen (Abb. 14).
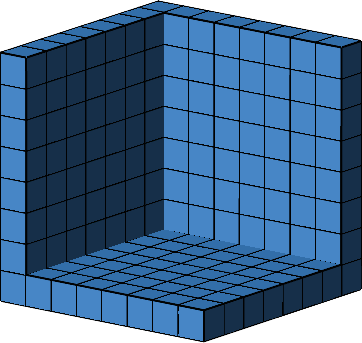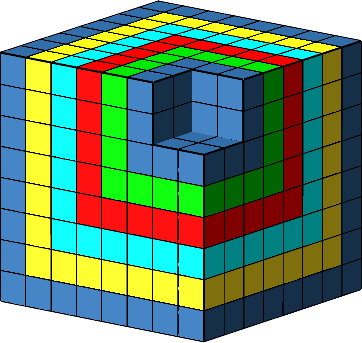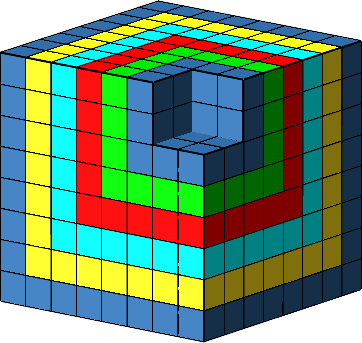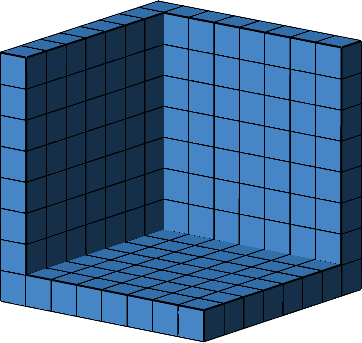
Abb. 14: Ineinanderlegen der räumlichen Ecken
Es entsteht ein großer Würfel (Abb. 15).
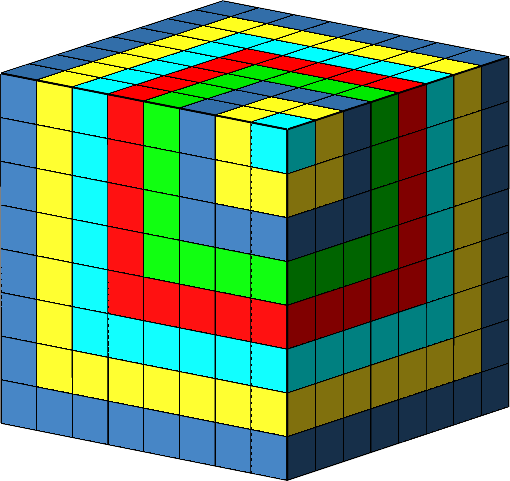
Abb. 15: Großer Würfel
Der große Würfel hat die Kantenlänge 8 und enthält somit 83 = 512 kleine Würfelchen.
Weblink
Hans Walser: Tausend
https://walser-h-m.ch/hans/Miniaturen/T/Tausend/Tausend.html