Hans Walser, [20210128], [2020203]
7 Dreiecke
1 Worum geht es?
Eine FlŠcheninvariante mit sieben gleichseitigen Dreiecken
2 Schritt um Schritt
Wir fźgen drei rote gleichseitigen Dreiecke an einer Ecke aneinander (Abb. 1).

Abb. 1: Drei rote gleichseitige Dreiecke
An die freien Au§enecken setzen wir blaue gleichseitige Dreiecke mit der Spitze nach innen an (Abb. 2).

Abb. 2: Drei blaue gleichseitige Dreiecke mit der Spitze nach innen
Dann gilt folgendes:
Die freien inneren Spitzen der blauen Dreiecke sind die Ecken
eines weiteren gleichseitigen Dreieckes.
Dieses zeichnen wir wieder rot (Abb. 3).
Wir haben also eine Art Schlie§ungsfigur mit sieben gleichseitigen Dreiecken.

Abb. 3: Siebentes gleichseitiges Dreieck. Rot = blau
Weiter gilt die FlŠchenbeziehung:
Die FlŠchensumme der vier roten Dreiecke ist gleich der
FlŠchensumme der drei blauen Dreiecke.
3 Beweise
Der Beweis ist eine idyllische RechenaffŠre.
Wir verwenden die Bezeichnungen der Abbildung 4.
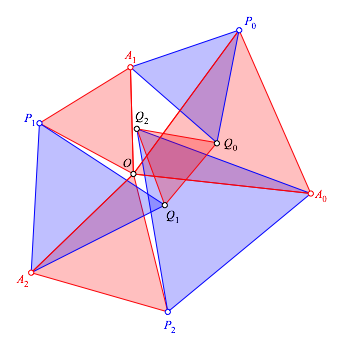
Abb. 4: Bezeichnungen
Der Startpunkt (gemeinsame Ecke der drei roten Startdreiecke) ist der Koordinatenursprung O.
Durch die Wahl von A0, A1 und A2 ist die ganze Konfiguration definiert.
Wir setzen:
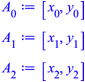
Zusammen mit dem Ursprung kšnnen wir die Punkte Pi berechnen:

Weiter berechnen wir die Punkte Qi:
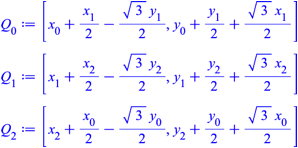
Wir berechnen die dritte Ecke Qfin des durch Q0 und Q1 definierten Dreiecks:
![]()
Wir sehen, dass dies mit Q2 źbereinstimmt. Damit ist die Schlie§ungseigenschaft gezeigt.
Fźr die FlŠchensumme der vier roten Dreiecke erhalten wir:
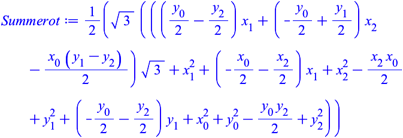
Fźr die FlŠchensumme der drei blauen Dreiecke entsprechend:
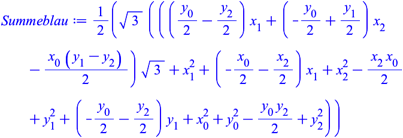
Die beiden FlŠchensummen sind gleich. Dies war zu zeigen.