Hans Walser, [20150307]

Ableitung der Sinusfunktion

1 Heuristisches Vorgehen

Zum Funktionsgraphen der Sinusfunktion werden die Steigungen graphisch ermittelt und als Funktion skizziert. Das legt die Vermutung nahe.

2 Einsicht und Beweis

Mit dem Additionstheorem für die Sinusfunktion erhalten wir:

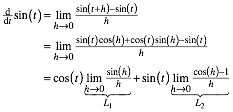
In beiden Limites haben wir eine „Null zu null“-Situation. Das mahnt zur Vorsicht.

2.1 Experimentell numerisches Vorgehen

Wir erhalten:

h
1.00000	0.84147	–0.45970
0.10000	0.99833	–0.04996
0.01000	0.99998	–0.00500
0.00100	1.00000	–0.00050
0.00010	1.00000	–0.00005
0.00001	1.00000	–0.00000

Tab. 1: Experiment

Auf Grund des Experimentes vermuten wir und . Damit haben wir erneut die Vermutung:

2.2 Beweis

2.2.1 Beweis für den ersten Grenzwert. Sandwichbeweis

Wir arbeiten mit den drei in der Abbildung 1 eingezeichneten Figuren.

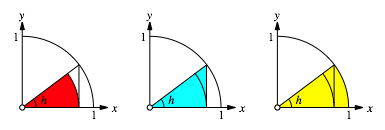
Abb. 1: Beweisfiguren

Die drei Figuren haben der Reihe nach die Flächeninhalte , und . Es ist auf Grund der Abbildung 1:

Daraus ergibt sich:

Für den Limes erhalten wir daher:

Dabei ist zu beachten, dass beim Grenzübergang die <-Relation durch die ≤-Relation zu ersetzen ist. Dies kann am Beispiel , aber eingesehen werden.

Somit ist eingeklemmt zwischen 1 und 1 und daher selber 1. Die Mathematiker verwenden für diesen Gedankengang die etwas widersprüchliche Formulierung „exakte Abschätzung“.

Aus folgt unmittelbar: . Wir werden diesen Sachverhalt im Folgenden verwenden.

2.2.2 Beweis für den zweiten Grenzwert

2.2.2.1 Geometrische Überlegung

Das grüne rechtwinklige Dreieck der Abbildung 2 hat die Hypotenusenlänge . Der kleinere der beiden spitzen Winkel ist . Daher misst die kurze Kathete .

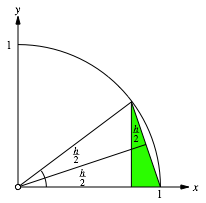
Abb. 2: Geometrische Überlegung

Andererseits ist die kurze Kathete auch . Somit haben wir:

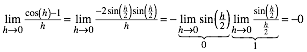
2.2.2.2 Berechnung mit Additionstheorem

Mit dem Additionstheorem für die Kosinusfunktion erhalten wir:

Somit ist:

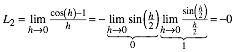
2.3 Zusammenfassung

Für die Ableitung der Sinusfunktion gilt daher:

Uff.