Hans Walser, [20230318]

Ableitungsfolge

1 Worum geht es?

Einheitliche Formel für die Ableitung einer gebrochen rationalen Funktion mit linearem Nenner.

2 Der Funktionsterm

Wir nehmen im Zähler ein Polynom vom Grad n und im Nenner einen linearen Term (Abb. 1 für n = 3).

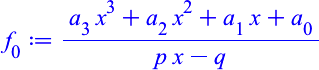
Abb. 1: Gebrochen rationaler Term

3 Ableitungen

Nun leiten wir ab. Die Abbildung 2 zeigt k und die k-te Ableitung nach x.

Abb. 2: Ableitungen

4 Feststellungen

Wir stellen fest, dass ab k = n die Terme eine einheitliche Form haben mit folgenden Eigenschaften:

· Alternierendes Vorzeichen (–1)^k

· Kein x im Zähler

· Koeffizient k! im Zähler

· Koeffizient p^k–n im Zähler

· Konstanter Koeffizient (Klammerausdruck) im Zähler. Der Klammerausdruck enthält die Koeffizienten des ursprünglichen Zählerpolynoms und homogene Ausdrücke n-ten Grades in p und q. Die Systematik ist offensichtlich.

· Im Nenner linearer Ausdruck (px – q) mit dem Exponenten k + 1.

5 Beweisskizze

Zunächst werden die x im Zähler „heruntergemacht“ (Ausdruck einer Schülerin). Ab dann induktiv.