Hans Walser, [20090124a]
Abnehmende Zickzacklinien
Anregung: R. E.
1 Fragestellung
Wie verhalten sich die beiden Zickzacklinien?
Harmonisch abnehmende Zickzacklinie
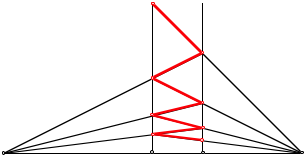
Exponentiell abnehmende Zickzacklinie
2 Bearbeitung
2.1 Harmonisch abnehmende Zickzacklinie
Wir
fźhren ein Koordinatensystem und Bezeichnungen gemŠ§ Arbeitsfigur ein. Gegeben
seien die drei Punkte 
, 
und 
sowie die Gerade q mit der Gleichung 
. Die Gerade p ist
die y-Achse.
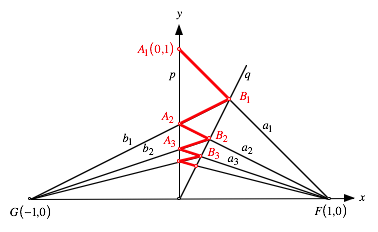
Arbeitsfigur
Wir
verbinden 
mit 
(Gerade 
) und schneiden mit q,
das gibt 
. Nun schneiden wir 
(Gerade 
) mit p und
erhalten 
. Schnitt von 
mit q gibt 
und so weiter.
Wir
erhalten dann der Reihe nach: 
, 
, 
, 
, ... . Allgemein
gilt:
Die y-Koordinaten bilden abnehmende harmonische Folgen.
Beweis induktiv:
(I) 
ist gegeben.
(II) Aus 
erhalten wir fźr
die Gerade 
die Gleichung 
. Schnitt mit der Geraden 
ergibt 
. Die Gerade 
hat dann die
Gleichung 
. Schnitt mit der Geraden 
liefert 
. Ł
2.2 Exponentiell abnehmende Zickzacklinie
Wir
fźhren wiederum ein Koordinatensystem und Bezeichnungen gemŠ§ Arbeitsfigur ein.
Die Nummerierung der Punkte 
und 
beginnt aus
Šsthetischen Grźnden mit Null. Gegeben seien die drei Punkte 
, 
und 
sowie die senkrechte
Gerade q mit der Gleichung 
. Die Gerade p ist
wiederum die y-Achse.
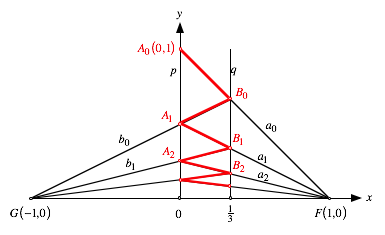
Arbeitsfigur
Wir
verbinden 
mit 
(Gerade 
) und schneiden mit q,
das gibt 
. Nun schneiden wir 
(Gerade 
) mit p und erhalten
. Schnitt von 
mit q gibt 
und so weiter.
Wir
erhalten der Reihe nach: 
(wie im oberen
Fall der harmonischen Zickzacklinie), 
(ebenfalls wie
oben), 
, 
, ... . Allgemein
gilt:
Die y-Koordinaten sind geometrische Folgen
mit dem Quotienten 
; wir haben also einen exponentiellen Zerfall.
Beweis induktiv:
(I) 
, also 
, ist gegeben.
(II) Auf
Grund der StrahlensŠtze ist 
, also 
. Weiter ist 
, also 
. Somit ist 
. Aus 
ergibt sich daraus
. Ł