Hans Walser, [20161103]
Abroll-Globus
1 Worum geht es?
Wir bauen einen Papierglobus, der abrollen lŠsst.
2 Kartengrundlagen
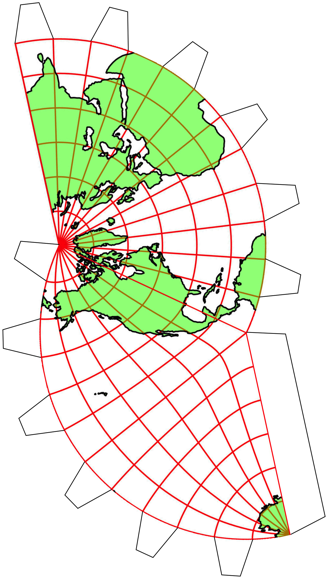
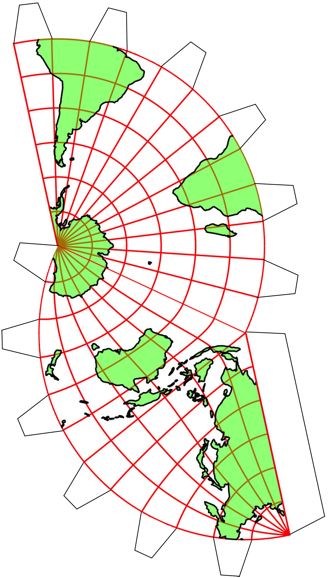
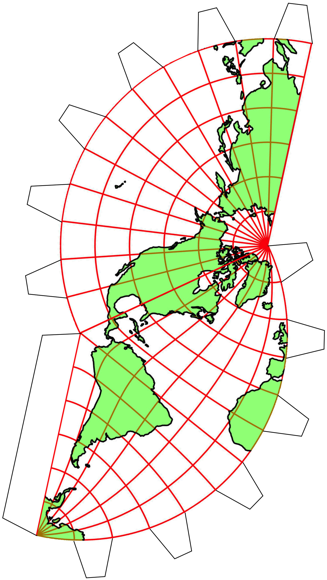
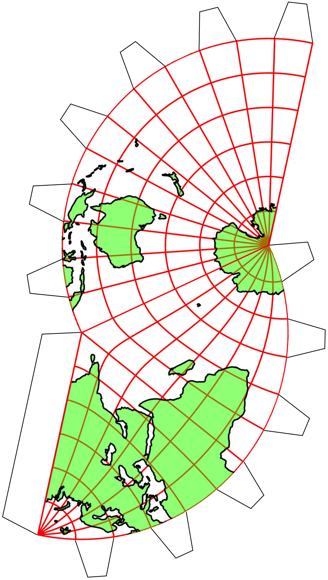
Die Abbildung 1 zeigt acht Kartenausschnitte. Jeder Ausschnitt zeigt einen Viertel der ErdoberflŠche. Die ganze Welt wird also insgesamt doppelt abgebildet. In der oberen Zeile erkennen wir in den Zentren der Bildpaare den Nordpol beziehungsweise den Sźdpol. Bei den Bildern der unteren Zeile kšnnen wir źber einen ăWestpolŇ und einen ăOstpolŇ nachdenken.
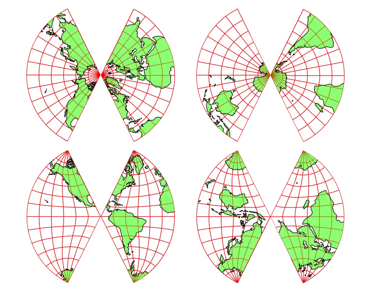
Abb. 1: Acht Kartenausschnitte
3 Zusammensetzen der Ausschnitte
Nun fźgen wir je vier der acht Ausschnitte so zusammen, dass es beim †bergang von einem zum nŠchsten Ausschnitt ăpasstŇ. Wir kšnnen das auf zwei Arten tun (Abb. 2).
In der Abbildung 2 sind fźr jede der beiden Weltkarten bereits die Klebelaschen und KlebezŠhne des zu bauenden Papiermodells eingezeichnet. Wir kšnnen aus jedem der beiden Schnittmuster einen Abroll-Globus bauen.
Die beiden Schnittmuster haben eine spiegelbildliche Form. Die Karteninhalte sind aber nicht spiegelbildlich.
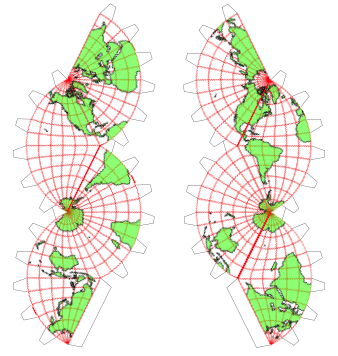
Abb. 2: Schnittmuster
Im Anhang sind die Schnittmuster in grš§erem Format wiedergegeben. Aus Platzgrźnden sind sie in je zwei Teilen angegeben. Daher ergibt sich eine zusŠtzliche Klebelasche.
4 Bauvorgang
Wir drucken zwei aufeinanderfolgende Schnittmusterteile des Anhangs aus und schneiden sie aus (Abb. 3 fźr das linke Beispiel der Abb. 2).

Abb. 3: Ausgeschnittene Teile
Der Rest ist Kleben. Wir verkleben mit einem Klebestift die beiden Teile lŠngs der langen Klebelaschen. Die langen Klebelaschen sind dazu nicht umzubiegen, da das Modell dort glatt ineinander źbergeht.
Wir haben jetzt ein zylinderfšrmiges Stźck mit zwei zueinander orthogonal stehenden MŠulern an den Enden. Wir biegen die ZŠhne leicht ein und kontrollieren, ob der Biss sitzt. Die ZŠhne mźssen wie die ZŠhne zweier ZahnrŠder ineinandergreifen. Dann betupfen wir bei einem der beiden MŠulern die ZŠhne mit einem schnellhŠrtenden Universalkleber, klappen zu, helfen allenfalls von innen und au§en ein bisschen nach und źben uns in Geduld, bis das Maul verklebt ist.
Mit dem zweiten Maul verfahren wir dann entsprechend. Da muss man das Modell mit sanftem Druck zwischen Daumen und Mittelfinger einige Minuten fixieren bis der Leim trocken ist.
Die Abbildung 4 zeigt das fertige Modell. Die eine Kante des Modells ist der halbe €quator von 90ˇW bis 90ˇE. Die andere Kante ist der 180ˇ-Meridian, also die Datumsgrenze.

Abb. 4: Abrollglobus
Die Abbildung 5 zeigt das Modell gemŠ§ dem rechten Schnittmuster der Abbildung 2. Es hat eine €quatorkante im Pazifik und eine Meridiankante beim Greenwich-Meridian.

Abb. 5: Zweites Modell
5 Bemerkungen
5.1 Geometrie des Abrollkšrpers
Wir beginnen mit einem Doppelkegel mit dem halben …ffnungswinkel 45ˇ (Abb. 6a).

Abb. 6: Zerschneiden des Doppelkegels
Der Achsenschnitt dieses Doppelkegels ist ein Quadrat. Wir zerschneiden den Doppelkegel mit einem Achsenschnitt und schieben die beiden hŠlften auseinander (Abb. 6b).
Nun verdrehen wir die hintere der beiden HŠlften um die Mittelnormale des Achsenschnittquadrates um 90ˇ (Abb. 7a).

Abb. 7: Verdrehen einer HŠlfte
Anschlie§end schieben wir die beiden HŠlften wieder zusammen und erhalten so den Abrollkšrper (Abb. 7b).
Die Abbildung 8 zeigt einen streifenweisen Zugang zum Abrollkšrper.
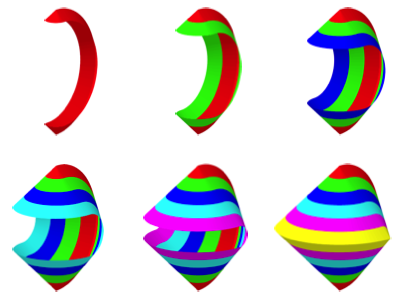
Abb. 8: Farbstreifen
5.2 Kartografisches
Bei den dargestellten Karten handelt es sich um Šquidistante Kegelprojektionen.
Fźr das
erste Bildpaar in der ersten Zeile der Abbildung 1 hat der Kegel die Spitze im
Nordpol und schneidet die Kugel im Breitenkreis ![]() . Das ist eine numerische Lšsung der Gleichung:
. Das ist eine numerische Lšsung der Gleichung:
![]() (1)
(1)
Damit erhŠlt der Kegel einen halben …ffnungswinkel von 45ˇ. Der Kegel hat dieselbe Achse wie die Erdkugel (normalachsige Kegelprojektion). Das gilt auch fźr das zweite Bildpaar in der ersten Zeile der Abbildung 1.
Die Bildpaare in der zweiten Zeile der Abbildung 1 sind querachsige Kegelprojektionen.
Das Wort Projektion bedeutet im kartografischen Kontext in der Regel keine Zentral- oder Parallelprojektion, wo die Bildgenerierung durch Projektionsstrahlen geschieht. Die Abbildungen sind vielmehr als Artefakte zu verstehen.
5.3 Vergleich mit dem Oloid
Unser Abrollkšrper ist nicht das von Paul Schatz 1929 eingefźhrte Oloid.
Es bestehen aber einige Gemeinsamkeiten. Beide Kšrper sind abrollbar. Ihre OberflŠche ist in die Ebene abwickelbar. Daher ist es mšglich, diese Kšrper als Papiermodelle zu bauen. Beide Kšrper haben eine so genannte RegelflŠche als OberflŠche. Wir kšnnen also Geraden in die OberflŠche einbauen. Bei unserem Abrollkšrper sind es die Mantellinien der Teilkegel.
Beide Kšrper haben in der OberflŠche zwei Kreisbšgen als Kanten. Die TrŠgerkreisebenen dieser Kreisbšgen stehen orthogonal aufeinander.
Der Unterschied betrifft die relative Lage der Zentren der beiden Kreisbšgen. In unserem Abrollkšrper sind die beiden Zentren identisch. Beim Oloid haben sie einen Abstand, der dem Bogenradius entspricht.
6 Websites
Kartenprojektionen (2. 11. 2016):
http://swai.ethz.ch/swaie/MapProjector/MapProjector.de.html
7 Anhang: Schnittmuster