Hans Walser, [20090427a]

Achteck

Anregung: Chr. W.

1 Worum es geht

Wir denken uns acht regelmäßig auf einem Kreis angeordnete Punkte.

Nun verbinden wir fortlaufend und insgesamt acht Mal Punkte in regelmäßigen Abständen. Dadurch entstehen, wenn die allenfalls mehrfach betroffene Punkte mit entsprechender Vielfachheit gezählt werden, Achtecke und/oder Sterne mit acht Spitzen. Wie groß sind deren Außen- und Innenwinkelsummen?

Ausgangslage

2 Verbinden der Punkte

2.1 Benachbarte Punkte, positiver Umlauf

Benachbarte Punkte, positiver Umlauf

Wir erhalten das reguläre Achteck.

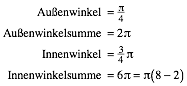
Bemerkung: Auf dem regulären Achteck haben zwei benachbarte Punkte den Bogenabstand . Das entspricht dem Außenwinkel.

2.2 Jeder zweite Punkt wird begrüßt

Wir verbinden jeden im positiven Umlaufssinn zweiten Punkt auf dem Kreis. Ausgehend von einem Startpunkt verbinden wir also fortlaufend Punkte mit dem Bogenabstand .

Jeder zweite Punkt kommt dran

Fürs Auge entsteht ein Quadrat, es ist aber doppelt durchlaufen und daher ein Achteck mit zweifachem Umlauf.

Es sind nur vier der acht Punkte betroffen, dafür diese doppelt. Das ist bei den entsprechenden Winkelsummen zu berücksichtigen.

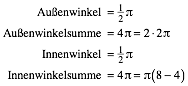
2.3 Jeder dritte Punkt

Ausgehend von einem Startpunkt verbinden wir fortlaufend Punkte mit dem Bogenabstand .

Jeder dritte Punkt

Wir erhalten einen schönen Stern.

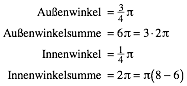
2.4 Jeder vierte Punkt

Wir verbinden Punkte mit dem Bogenabstand . Außer dem Startpunkt benötigen wir nur noch den diametralen Punkt.

Jeder vierte Punkt

Wir erhalten ein vierfach durchlaufenes Zweieck. Wow.

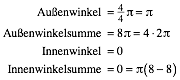
2.5 Jeder fünfte Punkt

Wir verbinden jeden fünften Punkt, im positiven Umlaufssinn gezählt. Das ist gleichbedeutend damit, dass wir jeden dritten Punkt im negativen Umlaufssinn nehmen.

Wir verbinden also Punkte mit dem Bogenabstand .

Jeder fünfte Punkt

Fürs Auge gibt das denselben Stern wie bei jedem dritten Punkt. Die Genesis läuft aber anders herum. Die beiden Sterne sind Spiegelbilder voneinander.

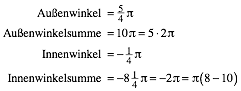
Spätestens an dieser Stelle wird man sich Gedanken machen müssen über die exakte Definition der Außen- und Innenwinkel.

Der Außenwinkel gibt die Richtungsänderung (orientierter, das heißt mit Vorzeichen versehener Winkel) an bei Übergang von einer Kante zur anschließenden Kante.

Den Innenwinkel berechnen wir als .

2.6 Jeder sechste Punkt

Nun ist es nicht mehr lustig. Wir verbinden Punkte mit dem Bogenabstand .

Jeder sechste Punkt

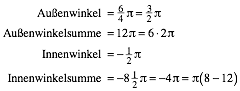
2.7 Jeder siebente Punkt

Jeder siebente Punkt

Wir erhalten das Spiegelbild des regulären Achteckes.

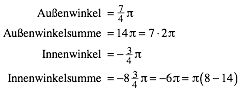
2.8 Jeder achte Punkt

Da läuft nichts mehr. Die Leserin ist aber eingeladen, sich zu überlegen, was geschieht, wenn wir jeden neunten Punkt nehmen.

3 Allgemein

3.1 Acht Punkte

Wir nehmen auf dem Kreis jeden k-ten Punkt (im positiven Drehsinn). Mit Vielfachheit gezählt erhalten wir eine Figur mit acht Ecken. Die Figur hat k Umläufe. Es ist:

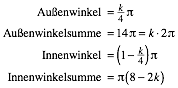
3.2 n Punkte

Wir beginnen mit n regelmäßig auf dem Kreis verteilten Punkten und verbinden dann jeden k-ten Punkt, . Insgesamt zeichnen wir n Verbindungen. Dann erhalten wir n-Ecke mit k Umläufen und:

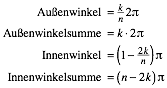
Wir sehen, dass die Formeln für die Außenwinkel viel einfacher sind. Vor allem die Außenwinkelsumme ist trivial, da wir k Umläufe haben.