Hans Walser, [20090928a]
Eine Figur mit acht plus einem Kreis
Anregungen: E. Chr. W. und P. G.
1 Worum geht es?
In der ebenen Geometrie scheinen sich Quadrat und regelmŠ§iges Dreieck zu ãbei§enÒ. Es ist unmšglich, ein regelmŠ§iges Dreieck in ein Quadratraster zu legen, und umgekehrt passt auch kein Quadrat in das regelmŠ§ige Dreiecksraster.
Gleichwohl gibt es eine auf Quadraten und Achtecken basierte Figur, welche regelmŠ§ige Dreiecke, Sechsecke, Zwšlfecke und ein 24-Eck enthŠlt. Die Figur enthŠlt zusŠtzlich einige schšne Eigenschaften. Historisch gesehen geht die Figur auf die Achteckskonstruktion in den BauhŸtten der mittelalterlichen Kathedralen zurŸck.
2 Aus der BauhŸtte
2.1 Die Konstruktion
In den BauhŸtten war folgende Konstruktion des Achteckes bekannt: Von den Ecken eines Quadrates aus werden vier Kreise durch den Quadratmittelpunkt geschlagen. Die Schnittpunkte dieser Kreise mit den Quadratseiten sind die Ecken eines regelmŠ§igen Achtecks.
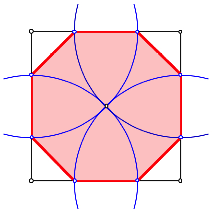
Konstruktion des Achteckes
2.2 Beweise
Rein logisch genŸgt natŸrlich ein Beweis. Wenn wir versuchen, mehrere Beweise zu finden, ergibt sich didaktischer Mehrwert (steuerfrei).
2.2.1 Forza brutale
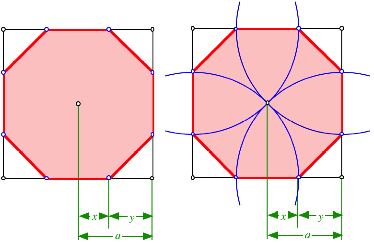
Bezeichnungen
Wir rechnen. Bezeichnungen gemŠ§ Figur. UnabhŠngig von der BauhŸttenkonstruktion gilt:
Daraus ergibt sich durch Elimination von y:
Aus der
BauhŸttenkonstruktion ergeben sich zwei Mšglichkeiten, den Kreisradius r auszudrŸcken: 
und 
. Gleichsetzen liefert:
Also dasselbe Resultat fŸr die halbe Achtecksseite x.
2.2.2 Elegante
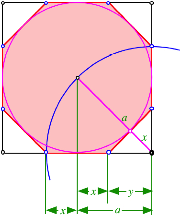
Beweisfigur
Diesen
schšnen Beweis verdanke ich Peter Gallin, ZŸrich. Der Kreisradius 
kann zum einen
auf der Quadratseite und zum anderen auf der Diagonalen eingesehen werden. Wenn
wir noch das um 45¡ verdrehte Quadrat einzeichnen, ergibt sich ein Proof
without Words.
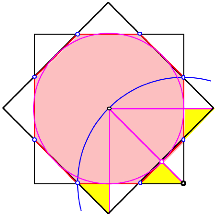
Proof w/o Words
2.3 Die Achtkreisfigur
Jetzt ist es wohl an der Zeit, die Achtkreisfigur anzusehen. Die Zentren der acht Kreisbogen sind die Ecken der beiden Quadrate. — VorlŠufig einfach eine Šsthetisch schšne Figur.
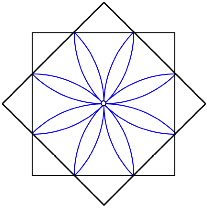
Achtkreisfigur
HŠtten wir etwas mehr Geduld gehabt und die Bogen bis zum Umkreis der Figur geschlagen, hŠtten wir acht gleichseitige Dreiecke gefunden.
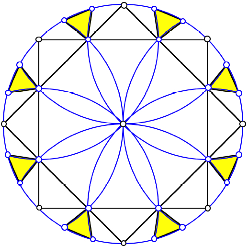
Acht kleine Dreiecke
Beweis: SŠmtliche neuen beteiligten Kreise haben denselben Radius. Es genŸgt also, zu zeigen, dass die an den Dreiecken beteiligten Kreisbogen denselben Zentriwinkel haben. Dieser Zentriwinkel ist 15¡, wie an der folgenden Figur eingesehen werden kann.
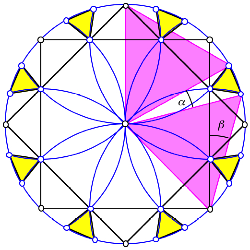
Beweisfigur
Die beiden magenta Dreiecke sind gleichseitig, ihre Winkel also 60¡. Daher gilt:
Wegen 
und der Symmetrie
der Figur bilden die 24 Punkte auf dem Umkreis ein regelmŠ§iges 24-Eck.
2.4 Das Zwšlfeck
Die acht Schnittpunkte dieses Umkreises mit den vier Kreisen ergeben zusammen mit den Quadratecken ein regelmŠ§iges Zwšlfeck. Die Punkte sind ja eine alternierende Auswahl aus den 24 Ecken des regelmŠ§igen 24-Eckes.
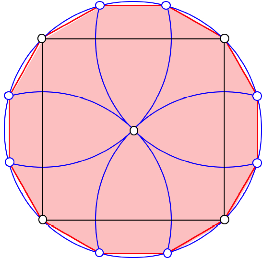
RegelmŠ§iges Zwšlfeck
Geben wir noch einen drauf und zeichnen die Kreise vollstŠndig. Das liefert erneut gleichseitige Dreiecke. Die an diesen Dreiecken beteiligten Kreisbogen haben den Zentriwinkel 30¡. Und wir kšnnen das Zwšlfeck zusammen mit den vier Dreiecken in ein Quadrat einpacken.
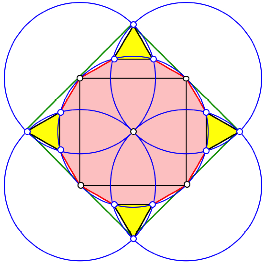
Mit Dreiecken und Au§enquadrat
3 Die kanonische Achtkreisfigur
Wir zeichnen acht kongruente Kreise, deren Zentren ein regelmŠ§iges Achteck mit einem neunten kongruenten Kreis als Umkreis bilden.
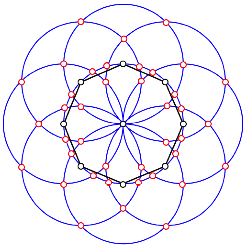
Acht Kreise und ein neunter
4 Vermutungen
Die wechselseitigen Schnittpunkte der Kreise sowie deren Zentren, also die Ecken des Ausgangsachteckes, lassen einige Vermutungen zu.
4.1 Das regelmŠ§ige 24-Eck
Wie wir schon gesehen haben, bilden die 24 Punkte auf dem Umkreis des Achteckes ein regelmŠ§iges 24-Eck. Durch Auswahl geeigneter Punkte erhalten wir also ein regelmŠ§iges Dreieck, ein Quadrat, ein regelmŠ§iges Sechseck und ein regelmŠ§iges Zwšlfeck. Das Achteck haben wir schon.
Als Beispiel ein regelmŠ§iges Dreieck.
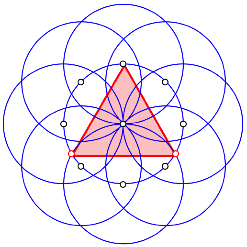
RegelmŠ§iges Dreieck
4.2 Die lieben Kleinen
Ganz neckisch sind die kleinen und ganz kleinen gleichseitigen Dreiecke. Wir haben diese in der BauhŸtte schon angetroffen.
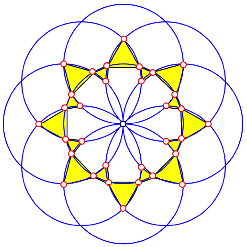
Zweimal acht kleine gleichseitige Dreiecke
4.3 Quadrate
Wir finden einen Kranz von Quadraten.
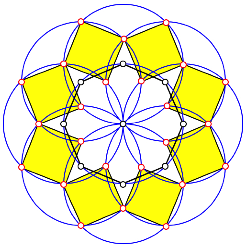
Quadrate
Um einzusehen, dass das wirklich Quadrate sind, ergŠnzen wir noch mit weiteren Vierecken.
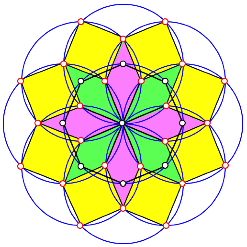
Rhomben
An der folgenden Figur kšnnen wir einsehen, dass es sich wirklich um Rhomben handelt. Sie haben den spitzen Winkel 45¡, die Seiten gehšren zu Kreisbogen mit dem Zentriwinkel 45¡.
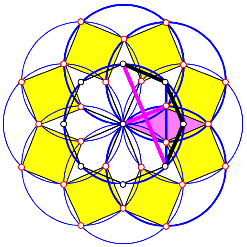
Beweisfigur
Die magenta Linien zeigen, dass die Schenkel des inneren gleichschenkligen Dreiecks der Vierecke zu Bšgen mit dem Zentriwinkel 45¡ gehšren. Die blaue Linie spiegelt das innere Dreieck auf das Šu§ere.
Mit einigen ZusatzŸberlegungen kann nun gezeigt werden, dass die gelben Vierecke rechtwinklige Rhomben derselben SeitenlŠnge sind, also Quadrate.
4.4 Kozyklische Punkte
Nun ja,
wir finden nun neun Kreise mit kleinerem Radius (der Radius ist 
mal der Radius
der bisherigen Kreise) welche durch mehrere Punkte unserer Figur laufen.
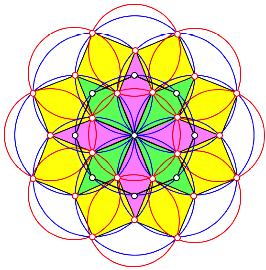
Noch mehr Kreise
4.5 Kollineare Punkte
Es gibt Tripel, Quadrupel, Quintupel und Hexatupel von kollinearen Punkten.
4.5.1 Punktetripel
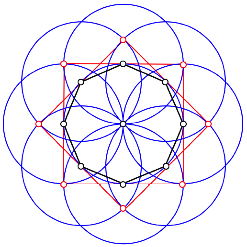
Kollineare Punktetripel
Die TrŠgergeraden der Punktetripel bilden zwei um 45¡ verdrehte Quadrate. Im Prinzip haben wir diese Konfiguration schon beim Zwšlfeck mit den aufgesetzten gleichseitigen Dreiecken angetroffen.
4.5.2 Punktequadrupel
Die folgenden zwei Figuren sind eine unmittelbare Folge der Figur mit den acht gelben Quadraten.
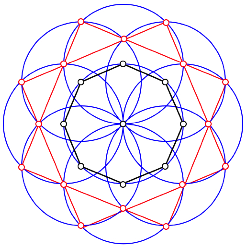
Kollineare Punktequadrupel
Die TrŠgergeraden bilden zwei um 45¡ verdrehte Quadrate.
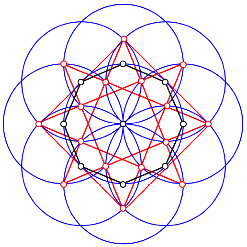
Eine zweite Schar von kollinearen Punktequadrupeln
Die TrŠgergeraden bilden einen achtspitzigen Stern.
4.5.3 Punktequintupel
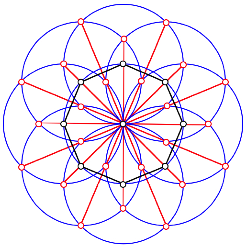
Kollineare Punktequintupel
Auf den Symmetrieachsen liegen je fŸnf Punkte.
4.5.4 Punktehexatupel
Auch diese Figur ergibt sich aus der Konfiguration mit den acht gelben Quadraten.
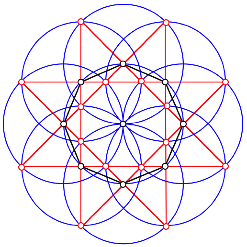
Kollineare Punktehexatupel
Die trŠgergeraden bilden einen achtspitzigen Stern.
4.5.5 Integrales Bild
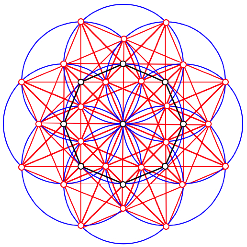
Kollineare Punkte mit TrŠgergeraden
4.6 Bild des 4D-HyperwŸrfels
Wir erkennen eine isometrische Darstellung des 4D-HyperwŸrfels. Die Figur ergibt sich aus der Figur mit den Punktehexatupeln.
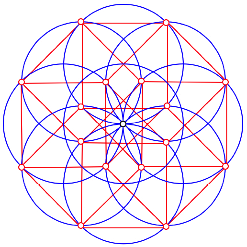
Bild des 4D-HyperwŸrfels