Hans Walser, [20131226]

Adam Ries

1 Worum geht es?

Es wird eine zufällig herausgegriffene Rechenaufgabe von Adam Ries untersucht. Dabei zeigt es sich, dass in der Lösungsmethode von Adam Ries spätere grafische und iterative Methoden implizit vorweggenommen sind.

2 Die Aufgabe

„Item / einer führet ghen Regenspurg von Wien 60. fuder Weins / gibt eins dem Zölner / von welchem er widerumb 30. flor. empfahet. Nun kompt ein ander bringt 200. fuder / gibt dem Zölner ein fuder vnd 20. fl. mehr. Die frag wie viel ein fuder ist werth gewesen? Setz 40. fl. sprich: 30. daruon / bleiben 10. die er dem Zölner gegeben hat / sprich: 60. geben 10. fl. was geben 200? Facit 33. fl. vnd ein drittheil / sollten 60. fl. sey / leugt zu wenig 26. fl. vnd 2/3. Setz fort / ein fuder kost 50. fl. Examinir auch / so kommen minus 3. fl. ein drittheil / die lügen resolvir in theil / steht also:

40 —— 80

70

50 —— 10

Vollfuehre es / kommen 51. fl. vnd . So viel hat ein fuder Weins gekost. „

(Ries Adam, 1574, S. 65, Rückseite)

3 Moderne Lösung

Da ich die von Adam Ries angegebene Lösung zunächst nicht verstand, versuchte ich es mit Methoden, wie sie heute in den Schulen unterrichtet werden:

x = Wert eines Fuders Wein

p = Zollanteil

Damit gilt:

60px = x – 30

200px = x + 20

Wir haben ein nicht lineares Gleichungssystem für x und p. Division ergibt:

Der Wert eines Fuders Wein ist (offenbar Druckfehler im Lösungsteil des Originaltextes). Weiter erhalten wir, was Adam Ries nicht gefragt hat, . Der Zoll beträgt einen Zwölftel von einem Zwölftel, also eins auf ein Gros.

4 Wie hat das Adam Ries gelöst?

Adam Ries arbeitet mit der Methode des „falschen Ansatzes“ (regula falsi): Es wird eine beliebige Zahl als Lösung für den Wert eines Fuders Wein untersucht. Sie wird sich als falsch erweisen, aber wir erhalten eine Information über den Fehler. Nun wird eine zweite Zahl versucht. Aus der Information über die Fehler der beiden Versuche erhalten wir einen Hinweis, wie wir korrigieren müssen, um auf die richtige Lösung zu kommen. Sprachlich muss im Konjunktiv gearbeitet werden.

In unserem Beispiel:

Wir versuchen es zunächst mit einem Wert von 40 fl. für ein Fuder Wein.

Damit ergäbe sich für den ersten Weinhändler einen Zoll vom Wert eines Fuders minus 30 fl., also 10 fl. .

Hochrechung (von 60 Fuder auf 200 Fuder) ergäbe für den zweiten Weinhändler einen Zoll von . Andererseits müsste er den Werte eines Fuders plus
20 fl. , also 60 fl. Zoll bezahlen. Der Vergleich ergibt einen Fehlbetrag von .

Nun versuchen wir es mit einem Wert von 50 fl. für ein Fuder Wein und rechnen analog durch.

Der erste Weinhändler müsste einen Zoll von 20 fl. zahlen. Hochrechnung auf den zweiten Händler ergäbe . Andererseits müsste er 70 fl. Zoll bezahlen. Der Fehlbetrag ist also noch

Jetzt fängt ein fröhliches Rechnen in Verhältnissen an. Die Drittel lässt Adam Ries daher weg (rechte Spalte in seiner tabellarischen Darstellung). Bei einer Erhöhung des virtuellen Wertes eines Fuders Wein um 10 fl. reduziert sich der Fehlbetrag um 70 Einheiten (die „Einheit“ ist jetzt ein Drittel). Da wir aber noch immer einen Fehlbetrag von 10 Einheiten haben, müssen wir den Wert von 50 fl. für ein Fuder Wein um erhöhen. Somit ist der wirkliche Wert eines Fuders Wein .

Bei dieser Rechnung wird stillschweigend angenommen, dass die Abnahme des Fehlbetrages linear von der Erhöhung des virtuellen Wertes abhängt. Die Abbildung 1 illustriert den Sachverhalt.

Solche grafische Verfahren wurden allerdings erst nach Adam Ries eingeführt, etwa von Descartes.

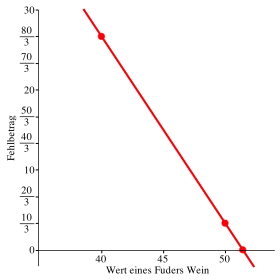
Abb. 1: Lineare Abhängigkeit

5 Alternativer Lösungsweg

Die Aufgabe von Adam Ries enthält zwei Unbekannte, nämlich den Wert eines Fuders Wein und den Zollansatz.

Adam Ries hat mit dem Wert eines Fuders Wein gespielt.

Wir können aber auch alternativ mit dem Zollansatz sielen und wählen also verschiedene Zahlen als virtuelle Zollansätze p.

Da für den ersten Weinhändler die Beziehung gilt, ergibt sich in Abhängigkeit von p für den Wert x eines Fuders Wein (der Index 1 soll andeuten, dass sich die Rechnung aus Sicht des ersten Weinhändlers ergibt):

Aus der Sicht des zweiten Weinhändlers ergibt wegen die Beziehung:

Beim richtigen Wert für p müssten x₁ und x₂ übereinstimmen, ihre Differenz also null sein.

Wir wählen nun für p die Werte der Tabelle 1, berechnen x₁ und x₂ sowie die Differenz.

p	p gekürzt	x1	x2	Differenz
29/4608		48.20084	77.31544	29.11460
30/4608	5/768	49.23077	66.20690	16.97613
31/4608		50.30568	57.88945	7.58377
32/4608	1/144	51.42857	51.42857	0.00000
33/4608	11/1536	52.60274	46.26506	-6.33768

Tab. 1: Verschiedene Werte für den Zollansatz

Wir sehen, dass p = 1/144 die richtige Lösung ist, mit x = 51.42857. Da in unserer Versuchsanordnung für p der richtige Wert auch vorhanden war, haben wir ihn entsprechend auch „gefunden“. Die Frage ist natürlich, wie wir vorgehen sollen, wenn wir keine Informationen über den richtigen Wert von p haben.

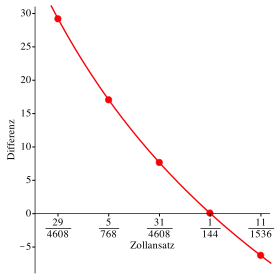
Abb. 2: Die Punkte liegen nicht auf einer Geraden

Die Punkte liegen nicht auf einer Geraden.

Wenn wir trotzdem auf Grund zweier Startwerte mit einer Geraden arbeiten, erhalten wir nicht den richtigen Wert für p, aber immerhin einen, der weniger falsch ist als die beiden Startwerte (Abb. 3).

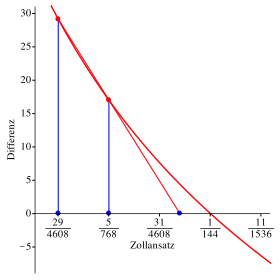
Abb. 3: Falscher Wert

Wir können nun das Verfahren gemäß Abbildung 4 mehrfach wiederholen und kommen dem richtigen Wert immer näher.

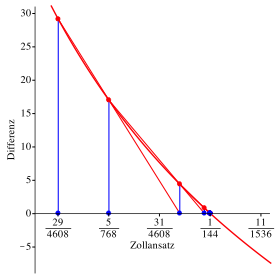
Abb. 4: Wiederholung des Verfahrens

Solche iterative Verfahren gehen auf Newton und Raphson zurück. Wir erhalten nie den exakten Wert, können aber den Fehler beliebig klein machen. Für praktische Zwecke ist dies gleich gut wie die Kenntnis des exakten Wertes.

Die Tabelle 2 gibt die Daten für p nach der Approximation gemäß der Abbildung 4 mit den beiden Startwerten p₁ = 29/4608 = 0.006293402778 und p₂ = 0.006510416667.

n	pn
1	0.006293402778
2	0.006510416667
3	0.006813919073
4	0.006919519207
5	0.006943079398
6	0.006944430397
7	0.006944444438

Tab. 2: Approximation des Zollansatzes

Wir sehen, dass sich die Werte dem richtigen Wert p = 1/144 = 0.006944444444 annähern.

6 Bemerkungen des Lehrers Lämpel

· Das Beispiel von Adam Ries arbeitet mit Verhältnissen.

· Die Idee des falschen Ansatzes ist eine Vorwegnahme eines heuristischen Problemlöseverhaltens.

· Die Idee des falschen Ansatzes ist auch eine Vorwegnahme von algorithmischen Approximationsverfahren.

· Das Beispiel ist von der Problemstellung her nicht authentisch, da jeder Weinhändler zwischen Wien und Regensburg über die Zolltarife im Bild war. Der Zollanteil von „eins auf ein Gros“ war ja leicht zu merken. Das Beispiel hat Übungs- und/oder Scherzfrage-Charakter.

· Das Beispiel ist vom Sachverhalt her nicht realistisch, da in Siebteln angegebene Preise wohl auch damals nicht üblich waren. Man rechnete allenfalls mit Sechsteln oder Zwölfteln.

· Das Beispiel ist von den numerischen Daten her didaktisch ungeschickt. Die Zahl 10 kommt in unterschiedlicher Bedeutung vor, einmal als Schrittgröße der virtuellen Werterhöhung, und dann aber auch als übrigbleibender Fehlbetrag (in Dritteln).

Literatur

Prinz, Ina: Rechnen wie die Meister. Die Rechenbücher von Johannes Widmann, Adam Ries, Christoff Rudolff und Johann Albrecht. Einführung zu den entsprechenden Faksimile Drucken. Arithmeticum Bonn. Nicolaische Verlagsbuchhandlung GmbH, Berlin 2009. ISBN 978-3-89479-492-7.

Ries, Adam: Rechenbuch auff Linien vnd Ziphren, in allerley Hanthierung, Geschäfften vnnd Kauffmanschafft, Mit neuwen künstlichen Regeln vnd Exempeln gemehret, Innhalt fürgestellten Registers. Visier vnd Wechselruthen künstlich vnd gerecht zumachen, auß dem Quadrat Durch die Arithmetic vnnd Geometri, von Erhart Helm, Mathematico zu Franckfurt, beschrieben. Alles von neuwem jetzunde wiederumb ersehen vnd Corrigiert. Franck. Bey. Chr. Egen. Erben. 1574. Frankfurt am Main.