Hans Walser, [20140817]
Additionstheorem fźr VerhŠltnisse im Dreieck
Herkunft: R., B.
1 Das Theorem
Die Abbildung 1 zeigt die geometrische Situation:
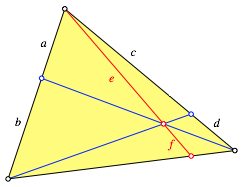
Abb. 1: Situation
Mit den Bezeichnungen der Abbildung 1 gilt:
![]()
2 Beweisskizze
Die Aussage des Theorems ist affin invariant. Wir kšnnen daher mit dem Dreieck der Abbildung 2 arbeiten.
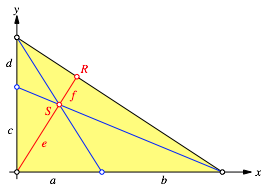
Abb. 2: Beweisfigur
Fźr den Schnittpunkt S erhalten wir mit einiger Rechnung die Koordinaten:
![]()
vom Punkt R benštigen wir nur die x-Koordinate:
![]()
Es ist dann:
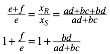
Somit ist:
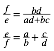
3 Eine Ungleichung
Wir verwenden die Bezeichnungen der Abbildung 3.
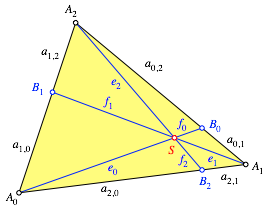
Abb. 3: Bezeichnungen
Dreimalige Anwendung des Additionstheorems liefert:
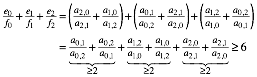
Gleichheit gilt genau dann, wenn S der Schwerpunkt ist.
4 Bemerkung
Das Theorem erinnert von ferne an den Satz von Ceva. Allerdings sind im Satz von Ceva die relevanten VerhŠltnisse multiplikativ verbunden.