Hans Walser, [20090418a]

Additionstheoreme

1        Herleitung an einem Dreieck

Wir arbeiten in einem Dreieck mit den Bezeichnungen der Figur. 

Bezeichnungsfigur

1.1      Additionstheorem fźr Sinus

Anregung von Chr. P., A.

 

 

 

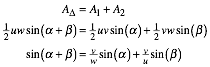
Nun ist aber  und . Eingesetzt ergibt:

 

 

1.2      Additionstheorem fźr den Kosinus

1.2.1    Direktes Vorgehen

Wir verwenden den Kosinussatz.

 

 

 

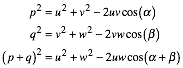
Andererseits ist aber:

 

 

Vergleich liefert:

 

 

 

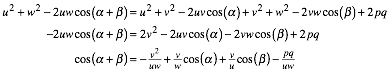
Wegen , ,  und  erhalten wir:

 

 

1.2.2    Basierend auf Additionstheorem fźr Sinus

Wir gehen davon aus, dass die Formel

 

gegeben ist. Das Additionstheorem fźr den Kosinus kšnnen wir daraus auf zwei verschiedenen Wegen herleiten. — Mit beiden Methoden kann auch umgekehrt das Additionstheorem des Sinus aus dem des Kosinus hergeleitet werden.

1.2.2.1  †berschieben

Wir verwenden die Relationen  und :

 

 

Bei dieser Herleitung wurde das Bogenma§ vorausgesetzt. Im Gradma§ muss  durch 90ˇ ersetzt werden.

1.2.2.2  Ableiten

Wir verwenden die Relationen  und . Wir leiten nun die Terme des Additionstheorems fźr den Sinus auf beiden Seiten partiell nach  ab:

 

 

Bei dieser Herleitung wurde das Bogenma§ vorausgesetzt. Bei Verwendung des Gradma§es erhalten wir auf beiden Seiten die innere Ableitung  als Faktor und mźssen dann durch diesen Faktor dividieren. — Derselbe Trick geht auch bei den Additionstheoremen der hyperbolischen Funktionen.

2        Herleitung źber Drehmatrizen

Die Additionstheoreme lassen sich einfach źber Drehmatrizen herleiten:

 

 

 

 

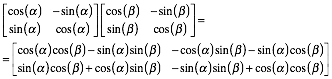
Andererseits ist die Zusammensetzung zweier Drehungen mit den Drehwinkeln  und  eine Drehung um . Daher ist:

 

 

Vergleich ergibt die Additionstheoreme fźr Kosinus und Sinus.