Hans Walser, [20140504]

Additionstheoreme

Ausarbeitung einer Idee von R. Sch., C.

1 Worum geht es?

Für gerades n gilt:

Für ungerades n gilt:

2 Eine Schließungsfigur

Wir zeichnen zwei Geraden, die sich unter einem Winkel von schneiden. Auf einer der beiden Geraden wählen wir einen Startpunkt und tragen die Einheitsstrecke abwechselnd auf den beiden Geraden ab. Dann ergibt sich eine Schließungsfigur mit (Hohenberg, 1979), (Walser, 1988).

Die Abbildung 1 zeigt exemplarisch für gerades n die Situation für .

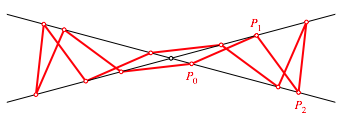
Abb. 1: n = 6

Die Abbildung 2 zeigt exemplarisch für ungerades n die Situation für .

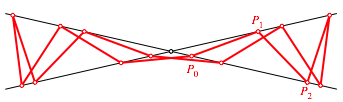
Abb. 2: n = 7

Wir sehen Unterschiede:

Für gerades n ist die Figur punktsymmetrisch. Das Symmetriezentrum ist der Schnittpunkt der beiden Geraden. Die konvexe Hülle des Streckenzuges ist ein Parallelogramm.

Für ungerades n ist die Figur achsensymmetrisch. Die Symmetrieachse ist die eine Winkelhalbierende der beiden Geraden. Die konvexe Hülle des Streckenzuges ist ein gleichschenkliges Trapez.

Es ist daher eine Fallunterscheidung bezüglich der Parität von n erforderlich.

Wir verwenden aber in beiden Fällen den Sonderfall, dass die konvexe Hülle ein Rechteck ist.

3 Gerades n

Die Abbildung 3 zeigt den Sonderfall mit einem Rechteck als konvexer Hülle des Streckenzuges.

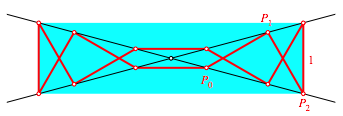
Abb. 3: Sonderfall für n = 6

Das Rechteck hat die Höhe 1 und die Länge s:

Mit einigen Winkelüberlegungen erhalten wir für die Seiten des Polygonzuges der Reihe nach die Steigungswinkel gegenüber der Basislänge des Rechtecks. Orthogonalprojektion auf diese Basislänge liefert (der letzte Summand ist de luxe und steht nur der Ästhetik halber da):

Wegen ergibt sich:

4 Ungerades n

Die Abbildung 4 zeigt wiederum den Sonderfall mit einem Rechteck als konvexer Hülle des Streckenzuges. In diesem Sonderfall ist der Startpunkt der Schnittpunkt der beiden Geraden.

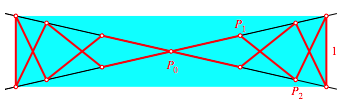
Abb. 4: Sonderfall für n = 7

Das Rechteck hat die Höhe 1 und die Länge s:

Mit einigen Winkelüberlegungen erhalten wir für die Seiten des Polygonzuges der Reihe nach die Steigungswinkel gegenüber der Basislänge des Rechtecks. Orthogonalprojektion auf diese Basislänge liefert:

Wegen ergibt sich:

Damit sind die Additionstheoreme des ersten Abschnittes bewiesen.

5 Link mit regelmäßigen Vielecken

Die Figur der Abbildung 3 lässt sich in ein regelmäßiges Zwölfeck einpacken (Abb. 5). Die Seiten des Polygonzuges sind parallel zu den Zwölfeckseiten.

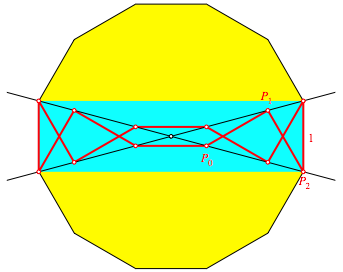
Abb. 5: Zwölfeck

Entsprechend lässt sich die Figur der Abbildung 4 in ein regelmäßiges 14-Eck einpacken (Abb. 6).

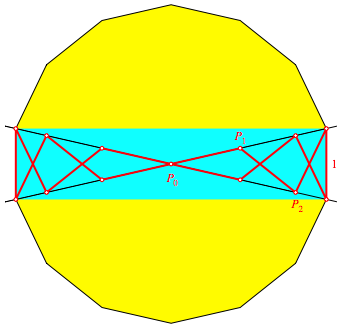
Abb. 6: 14-Eck

Damit ergeben sie wohl einfachere Beweismöglichkeiten für unsere Summen und analoge Summen mit Sinuswerten, vgl. (Götzl und Walser, 2012).

Literatur

Götzl, Dieter und Walser, Hans (2012): Abstandssummen am regelmäßigen n-Eck. MNU. Der mathematische und naturwissenschaftliche Unterricht 65/8 (1. 12. 2012), 465-467. ISSN 0025-5866.

Hohenberg, Fritz (1979): Gleichseitige Polygone, deren Ecken abwechselnd auf zwei Geraden liegen. Sitzungsberichte der Österreichischen Akademie der Wissenschaften, Mathematisch naturwissenschaftliche Klasse, Abteilung II, 188. Band, 385-405.

Walser, Hans (1988): Ein Schliessungssatz der Elementargeometrie. Elemente der Mathematik (43), 161-169.