Hans Walser, [20140504a]

Additionstheoreme

Ausarbeitung einer Idee von R. Sch:, C.

1 Worum geht es?

Anhand des regelmäßigen 2n-Eckes werden acht trigonometrische Summenformeln hergeleitet. Dabei ist eine Paritätsunterscheidung bezüglich n erforderlich.

2 Gerades n

Die Eckenzahl 2n ist also durch vier teilbar.

2.1 Basislinie horizontal

Wir arbeiten zunächst mit dem regelmäßigen 2n-Eck gemäß Abbildung 1. In der Abbildung 1 ist .

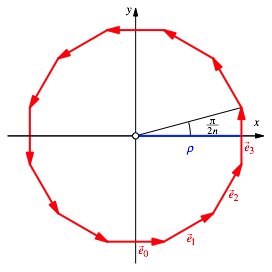
Abb. 1: Überlegungsfigur

Die eingezeichneten Vektoren sind Einheitsvektoren, also:

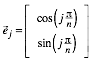
Für den Inkreisradius erhalten wir:

Den Inkreisradius können wir auch durch Projektionen von geeigneten Einheitsvektoren auf die x-Achse ausdrücken (Abb. 2).

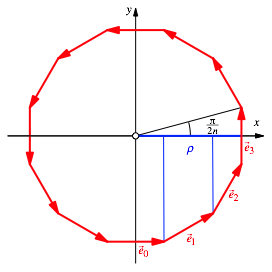
Abb. 2: Projektionen

So erhalten wir:

(1)

Durch analoge Projektion auf die y-Achse ergibt sich:

(2)

2.2 Spitzständig

Wir drehen das regelmäßige 2n-Eck der Abbildung 1 um . Dadurch erhalten wir ein regelmäßiges 2n-Eck, das auf einer Spitze steht (Abb. 3).

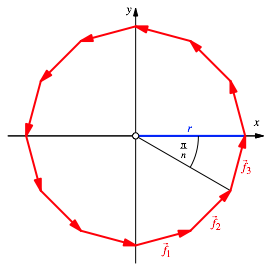
Abb. 3: Spitzständiges 2n-Eck

Die eingezeichneten Vektoren sind Einheitsvektoren, also:

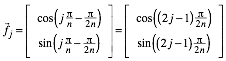
Für den Umkreisradius r erhalten wir:

Durch Projektion auf die x- beziehungsweise y-Achse ergeben sich die Formeln:

(3)

(4)

3 Ungerades n

Die Eckenzahl 2n ist nun kongruent 2 modulo 4. Die Abbildungen illustrieren den Fall .

3.1 Bodenständig

Die Abbildung 4 illustriert den Fall mit horizontaler Basislinie.

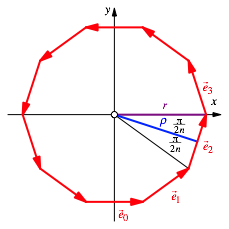
Abb. 4: Ungerades n. Horizontale Basislinie

Für die Einheitsvektoren gilt wiederum:

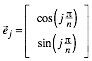
Für den Umkreisradius r erhalten wir ebenfalls:

Für den Inkreisradius erhalten wir wiederum:

Projektionen ergeben:

(5)

(6)

3.2 Spitzständig

Wir drehen um und erhalten die Figur der Abbildung 5.

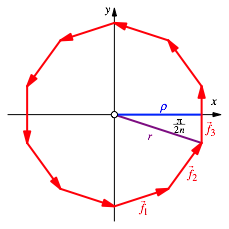
Abb. 5: Ungerades n. Spitzständig

Die eingezeichneten Vektoren sind Einheitsvektoren, also:

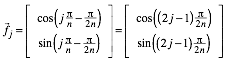
Durch Projektion erhalten wir:

(7)

(8)