Hans Walser, [20180823]

Äquidistanz

Anregung: Schröpfer 2018

1 Worum geht es?

Spiel mit äquidistanten Kreisen und Geraden. Hintergrund: Kegelschnitte.

2 Ellipse

Wir beginnen mit zwei äquidistanten Kreistripeln mit den Zentren F und G (Abb. 1).

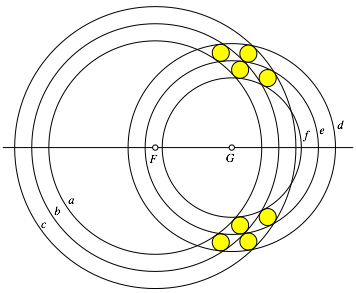
Abb. 1: Kreistripel

Dann wählen wir sechs Schnittpunkte gemäß Abbildung 2. Diese sechs Schnittpunkte liegen auf einer Ellipse mit den Brennpunkten F und G (Fadenkonstruktion).

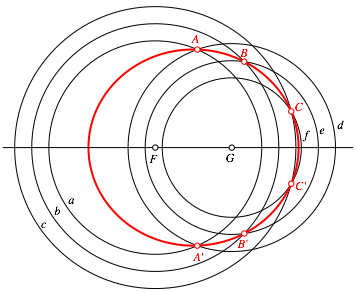
Abb. 2: Schnittpunkte und Ellipse

Die Ellipsensehnen gemäß Abbildung 3 sind aus Symmetriegründen parallel.

Diese Ellipsensehnen sind äquidistant.

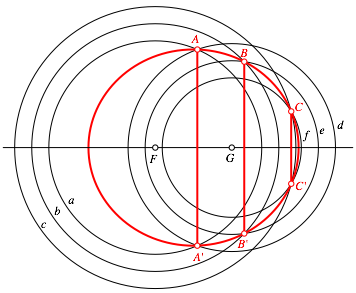
Abb. 3: Äquidistante Ellipsensehnen

3 Beweise

3.1 Rechnerischer Beweis

Wir wählen eine Koordinatensystem so dass und . Die Kreise haben dann der Reihe nach die Gleichungen:

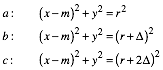(1)

und

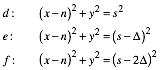(2)

Dabei ist der Unterschied zwischen den Kreisradien.

Da die Sehnen senkrecht zur x-Achse stehen, genügt es, zu zeigen, dass die x-Koordinaten der Punkte A, B und C eine arithmetische Folge bilden.

Der Punkt A ist ein Schnittpunkt der Kreise a und d, also:

(3)

Durch Subtraktion der beiden Gleichungen erhalten wir:

(4)

Der Punkt B ist ein Schnittpunkt der Kreise b und e. Eine zu (3) und (4) analoge Rechnung liefert:

(5)

Für C erhalten wir schließlich:

(6)

Dies war zu beweisen.

3.2 Raumgeometrische Überlegung

Wir interpretieren die konzentrischen Kreise als Niveaulinien von Kegeln. Diese beiden Kegel haben gleich steile Mantellinien, aber der eine hat die Spitze oben und der andere unten (Abb. 4).

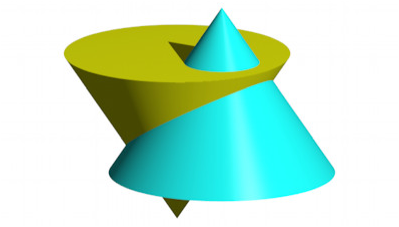
Abb. 4: Die beiden Kegel

Die Schnittkurve der beiden Kegel ist eine Ellipse (Abb. 5).

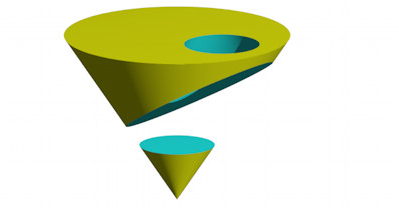
Abb. 5: Schnittkurve eine Ellipse

Diese Ellipse liegt in einer schrägen Ebene. In der Abbildung 3 sehen wir diese Ellipse von oben. Die Sehnen sind die Niveaulinien der schrägen Trägerebene der Ellipse.

4 Hyperbel

Die Abbildung 6 zeigt eine Modifikation der Abbildung 3. Statt einer Ellipse haben wir eine Hyperbel. Die Hyperbelsehnen sind äquidistant.

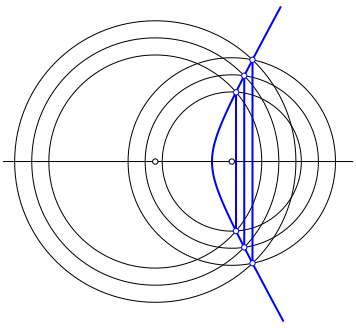
Abb. 6: Hyperbel

Die Beweise laufen analog. Bei der räumlichen Überlegen haben die beiden Kegel entweder beide die Spitze oben oder beide die Spitze unten (Abb. 7 und 8).

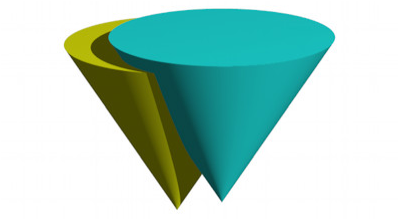
Abb. 7: Beide Spitzen unten

Abb. 8: Hyperbel als Schnittfigur

Die Trägerebene der Hyperbel ist sehr steil, wie ein Blick von der Seite zeigt (Abb. 9). Daher sind auch die Niveaulinien so nahe beieinander (Abb. 6).

Abb. 9: Blick von der Seite

Literatur

Schröpfer, Gerhard (2018): Aufgabe 24.3. IBDG, Informationsblätter der Geometrie, Heft 1/2018, Jahrgang 37, S. 9.