Hans Walser, [20150418]
Affine und projektive Kegelschnittbilder
Anregung: H. H., W.
1 Worum geht es?
Wir wollen zeigen, dass das affine Bild einer Ellipse wieder eine Ellipse, das affine Bild einer Parabel wieder eine Parabel und das affine Bild einer Hyperbel eine Hyperbel ist.
Das ist nicht trivial, da fŸr projektive Abbildungen dieser Sachverhalt nicht gilt. Dies wird exemplarisch gezeigt.
2 Affine Abbildung
Eine regulŠre affine Abbildung hat lineare Abbildungsgleichungen
mit
.
Der Vektor
ist der Translationsanteil, der fŸr unsere †berlegungen weggelassen werden kann. Somit bleiben die Abbildungsgleichungen:
Wir brauchen rechentechnisch im Folgenden die Umkehrabbildung:
(1)
2.1 Allgemeine Gleichung zweiten Grades
Eine allgemeine Gleichung zweiten Grades ist von der Form:
(2)
In Gro§vaters Formelsammlung (DMK/DPK 1992, S. 71) finden wir folgende Klassifizierung:
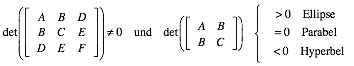(3)
sowie
Da eine affine Abbildung geradentreu ist, kšnnen wir den zweiten Fall fŸr unsere †berlegungen weglassen.
2.2 Etwas Rechnung
Wir setzen (1) in (2) ein:
Die lŠsst sich umformen zu:
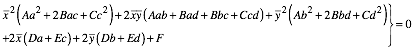
Mit
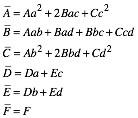
erhalten wir wiederum die Form (2).
FŸr das entscheidende Kriterium gemŠ§ (3) ergibt sich:
Dies lŠsst sich umformen zu:
Der
Faktor 
ist das
Quadrat der inversen Abbildungsdeterminante. Bei einer regulŠren Abbildung ist
diese nicht null, das Quadrat davon also positiv. Daher haben die Determinanten
und 
das
gleiche Vorzeichen. GemŠ§ (3) ist also die Aussage im ersten Abschnitt
bewiesen.
3 Beispiel einer projektiven Abbildung
Wir werden exemplarisch zeigen, dass der Sachverhalt bei projektiven Abbildungen viel interessanter ist.
Eine projektive Abbildung hat gebrochen lineare Abbildungsgleichungen. Wir arbeiten mit dem Beispiel:
Diese Abbildung hat zunŠchst die x-Achse als Fixpunktgerade.
Nullsetzen
des gemeinsamen Nenners in den Abbildungsgleichungen liefert die so genannte Verschwindungsgerade. In unserem Beispiel
ist das die Gerade 
(Abb. 1).
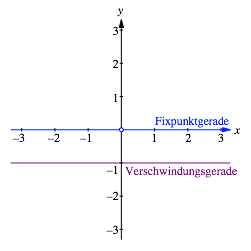
Abb. 1: Fixpunktgerade und Verschwindungsgerade
Die Punkte auf dieser Geraden werden in unendlich ferne Punkte abgebildet (ãDivision durch nullÒ). Das Bild der Verschwindungsgeraden ist entsprechend die unendlich ferne Gerade.
FŸr die Rechnungen benštigen wir wiederum die Abbildungsgleichungen der Umkehrabbildung. Diese sind:
3.1 Bild des Einheitskreises
Der
Einheitskreis 
berŸhrt
die Verschwindungsgerade. Dieser Punkt muss also verschwinden.
Rechnerisch erhalten wir:
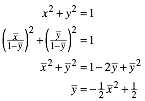
Das ist die Gleichung einer Parabel (Abb. 2).
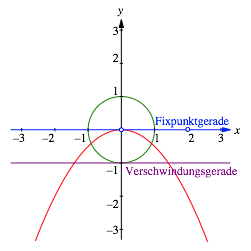
Abb. 2: Parabel
3.2 Bild des Kreises mit Radius ½
Der Kreis
hat mit
der Verschwindungsgeraden keinen Punkt gemeinsam. Da kann nicht viel passieren.
Rechnerisch erhalten wir (die ãquadratische ErgŠnzungÒ ist immer wieder
spannend):
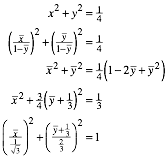
Das ist die Gleichung einer Ellipse (Abb. 3).
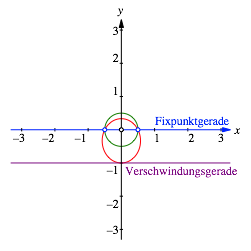
Abb. 3: Ellipse
Wir sehen, dass Urbild (dunkelgrŸn) und Bild (rot) sich auf der Fixpunktgeraden schneiden.
Dass die
rote Bildellipse die Verschwindungsgerade berŸhrt, hat nichts zu bedeuten, da
die Verschwindungsgerade zum Urbildgehšrt. Das ist also reiner Zufall. Wenn wir
jetzt allerdings die rote Ellipse abbilden, erhalten wir eine Parabel, nŠmlich 
. Auch diese geht durch die gemeinsamen Fixpunkte.
3.3 Bild des Kreises mit Radius 2
Der Kreis
schneidet
die Verschwindungsgerade in zwei Punkten.
Rechnerisch erhalten wir:
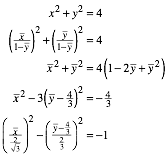
Das ist die Gleichung einer Hyperbel (Abb. 4).
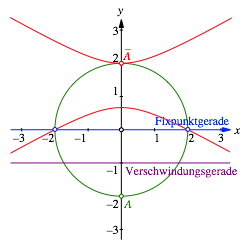
Abb. 4: Hyperbel
Der
Urbildkreis und die Hyperbel schneiden sich auf der Fixpunktgeraden. Dass die
Hyperbel und der Urbildkreis sich oben berŸhren, ist ein unglŸcklicher Zufall.
Auf Grund der Abbildungsgleichungen ist nŠmlich 
.
Die Abbildung 5 illustriert, wie die Schnittpunkte des Urbildkreises mit der Fixpunktgeraden (das sind die Punkte, die ins Unendliche abrauschen) mit den Asymptoten der Hyperbel zusammenhŠngen. Sie legen die Richtungen der Asymptoten fest.
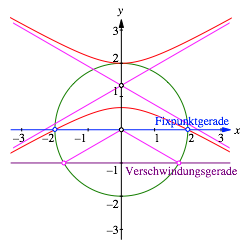
Abb. 5: Asymptoten
3.4
RŽsumŽ
Das Bild eines Kreises als Sonderfall einer Ellipse kann bei ein und derselben projektiven Abbildung eine Parabel, eine Ellipse oder eine Hyperbel sein. Entscheidend ist, ob der Kreis die Verschwindungsgerade berŸhrt, meidet oder schneidet.
4 Philosophisches
Was auf der Verschwindungsgeraden liegt, geht sozusagen dann hinter die Kulissen. Bei einer affinen Abbildung bleibt alles auf der BŸhne, was auf der BŸhne ist. Und alles, was hinter den Kulissen ist, bleibt dort. Die unendlich ferne Gerade ist bei affinen Abbildungen eine Fixgerade (zum Beispiel bei Drehungen) oder gar eine Fixpunktgerade (zum Beispiel bei Translationen oder zentrischen Streckungen).
Eine Parabel ist eine an sich geschlossene Kurve, die mal kurz hinter den Kulissen die unendliche ferne Gerade kŸsst.
Literatur
DMK/DPK (1992): Deutschschweizerische Mathematikkommission / Deutschschweizerische Physikkommission: Formel und Tafeln. Mathematik – Physik. 5. Auflage. ZŸrich: Orell FŸssli. ISBN 3 280 02162 6.