Hans Walser, [20191219]
Das Theorem des Al-Sijzī
1 Worum geht es?
Es wird ein Theorem des persischen Mathematikers Al-Sijzī (zweite HŠlfte des 10. Jahrhunderts) vorgestellt.
2 Beliebiges Dreieck
Wir beginnen mit einem beliebigen Dreieck ABC (Abb. 1). Weiter sei M der Mittelpunkt der Strecke AB und s die von C ausgehende Seitenhalbierende.
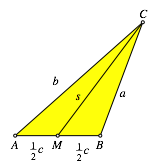
Abb. 1: Dreieck
Wir fźhren Vektoren ein gemŠ§ Abbildung 2.
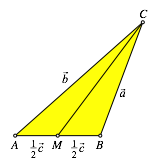
Abb. 2: Vektoren
Es ist:
(1)
Daraus ergibt sich:
(2)
Addition liefert:
(3)
In der Schreibweise ohne Vektoren hei§t dies:
(4)
Dies ist das Theorem des Al-Sijzī.
Wenn nun die Punkte A und B fest bleiben und C auf dem Kreis um M mit Radius s variiert, bleibt die rechte Seite von (4) invariant. Damit ist aber auch die QuadratflŠchensumme auf der linken Seite von (4) invariant.
Die Abbildung 3 illustriert den Sachverhalt.
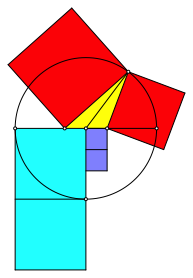
Abb. 3: Theorem des Al-Sijzī: Rot = blau
Die FlŠchensumme der beiden roten Quadrate entspricht der FlŠchensumme der vier blauen und hellblauen Quadrate.
Die Abbildung 4 zeigt einen Zerlegungsbeweis fźr das Beispiel der Abbildung 3.
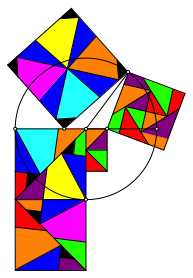
Abb. 4: Zerlegungsbeweis
Die Abbildung 5 zeigt ein Beispiel mit einem stumpfen Winkel bei C.
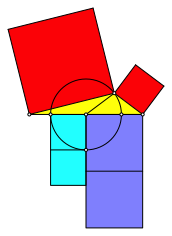
Abb. 5: Oben ein stumpfer Winkel
3 Sonderfall
Fźr 
ergibt
sich der Satz des Pythagoras. Der Kreis wird zum Thaleskreis.
4 Umbau
Die Figur der Abbildung 3 lŠsst sich umbauen zur Figur der Abbildung 6. Dazu wird das gelbe Dreieck der Abbildung 3 mit der Seitenhalbierenden halbiert und die beiden HŠlften werden neu zusammengesetzt.
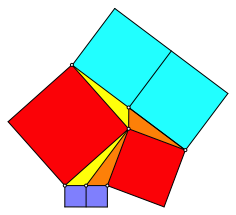
Abb. 6: Rot = blau
Die Abbildung 7 zeigt den entsprechenden Umbau der Abbildung 5.
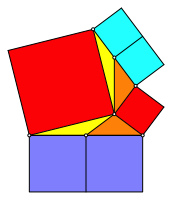
Abb. 6: Rot = blau
5 Ganzzahlig
Es gibt auch, entsprechend zu den pythagoreischen Tripeln, ganzzahlige Lšsungen. Die Tabelle 1 gibt einige Beispiele.
|
a |
b |
c |
s |
Bemerkungen |
|
5 |
5 |
6 |
4 |
Aus pythagoreischen Dreiecken zusammengesetzt |
|
5 |
5 |
8 |
3 |
Aus pythagoreischen Dreiecken zusammengesetzt |
|
6 |
8 |
10 |
5 |
Pythagoreisches Dreieck |
|
7 |
9 |
8 |
7 |
Abb. 8 |
|
7 |
9 |
14 |
4 |
Abb. 9 |
|
7 |
11 |
12 |
7 |
|
|
7 |
11 |
14 |
6 |
|
|
8 |
14 |
14 |
9 |
|
|
8 |
14 |
18 |
7 |
|
|
9 |
13 |
10 |
10 |
|
|
9 |
13 |
20 |
5 |
|
|
9 |
17 |
16 |
11 |
|
|
9 |
19 |
20 |
11 |
|
|
10 |
10 |
12 |
8 |
Aus pythagoreischen Dreiecken zusammengesetzt |
|
10 |
10 |
16 |
6 |
Aus pythagoreischen Dreiecken zusammengesetzt |
|
10 |
20 |
18 |
13 |
|
|
11 |
13 |
16 |
9 |
|
|
11 |
13 |
18 |
8 |
|
|
11 |
17 |
12 |
13 |
|
|
12 |
14 |
14 |
11 |
|
|
12 |
16 |
20 |
10 |
Pythagoreisches Dreieck |
|
13 |
13 |
10 |
12 |
|
|
14 |
18 |
16 |
14 |
|
|
15 |
15 |
18 |
12 |
Aus pythagoreischen Dreiecken zusammengesetzt |
|
17 |
17 |
16 |
15 |
Aus pythagoreischen Dreiecken zusammengesetzt |
|
17 |
19 |
12 |
17 |
|
|
17 |
19 |
20 |
15 |
|
Tab. 1: Ganzzahlige Lšsungen
Abb. 8: Ganzzahliges Beispiel
Abb. 9: Ganzzahliges Beispiel
Websites
Hans
Walser: Al-Sijzī
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi/Al-Sijzi.htm
Hans Walser: Pythagoras-Schmetterling
www.walser-h-m.ch/hans/Miniaturen/P/Pythagoras-Schmetterling/Pythagoras-Schmetterling.htm