Hans Walser, [20200101]

Al-Sijzi

Anregung: Z. D., W.

1 Worum geht es?

Kugelproblem. Etwas Rechnung.

Die Idee geht auf al-Sijzi (945-1020) zurück.

2 Problemstellung

Im n-dimensionalen Raum seien m Punkte gegeben.

Gesucht ist die Menge der Punkte mit der Eigenschaft:

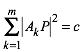(1)

Dabei ist c eine Konstante.

3 Bearbeitung

Die Bedingung (1) lautet in Koordinaten:

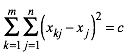(2)

Mit einiger Rechnung lässt sich (2) umformen zu:

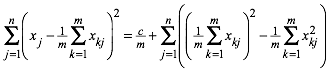(3)

Dies ist die Gleichung einer Hyperkugel im n-dimensionalen Raum. Die Hyperkugel hat den Mittelpunkt M:

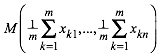(4)

Dies ist der Schwerpunkt der m Punkte .

Weiter hat die Hyperkugel den Radius r:

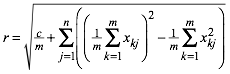(5)

4 Beispiel

Es sei n = 3 und m = 3 und weiter:

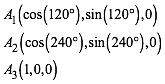(6)

Weitere sei c = 6. Für (3) ergibt sich mit CAS die Kugelgleichung:

(7)

Die Abbildung 1 illustriert den Sachverhalt.

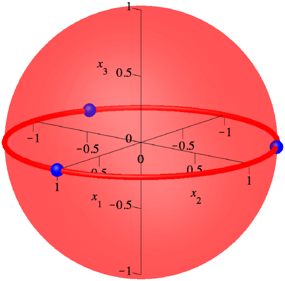
Abb. 1: Kugel

Die drei blauen Punkte auf dem Äquator sind die durch (6) gegebenen Punkte.

Kontrollen:

Ist P einer der drei blauen Punkte, haben wir die Abstände . Die Summe der Quadrate der Abstände ist 6.

Ist P der Nordpol, haben wir dreimal den Abstand . Die Summe der Quadrate der Abstände ist 6.

Ist (hinten auf dem Äquator), haben wir die Abstände 1, 2, 1. Die Summe der Quadrate der Abstände ist 6.

Websites

Hans Walser: Al-Sijzi

http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi2/Al-Sijzi2.htm