Hans Walser, [20210104]
Al-Sijzi
Anregung: Johanna Heitzer, Aachen
Mathematik ist das Finden von Invarianten.
Heinz Hopf
1 Worum geht es?
Verallgemeinerung der Stze von Pythagoras und al-Sijzi sowie des Begriffs des Thaleskreises. Invarianten.
2 Problemstellung
Gegeben seien m Punkte Ai im Rn.
Zu einer gegebenen Konstanten k suchen wir die Punktmenge H:
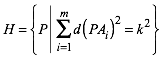 (1)
(1)
Die Summe der Quadrate der Abstnde von P zu Ai soll konstant k2 sein.
Das hei§t
umgekehrt, dass fr alle Punkte ![]() die Summe
der Quadrate der Abstnde invariant bleibt.
die Summe
der Quadrate der Abstnde invariant bleibt.
3 Behauptung
Die gesuchte Punktmenge H ist eine n–1-Hypersphre um den Schwerpunkt S der m Punkte Ai. Der Beweis folgt sogleich. Beispiele anschlie§end.
4 Beweis
Wir whlen ein kartesisches Koordinatensystem so, dass der Schwerpunkt S der m Punkte Ai in den Nullpunkt zu liegen kommt.
Mit ![]() gilt dann
die Schwerpunktbedingung:
gilt dann
die Schwerpunktbedingung:
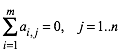 (2)
(2)
Mit ![]() , erhalten wir fr das Quadrat eines
einzelnen Abstands:
, erhalten wir fr das Quadrat eines
einzelnen Abstands:
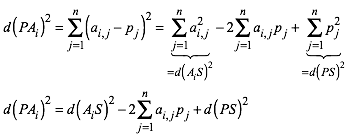 (3)
(3)
Fr die Summe der Quadrate der Abstnde folgt daraus:
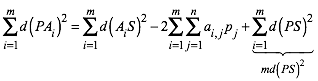 (4)
(4)
Durch Vertauschung der Summationsreihenfolge in der Doppelsumme ergibt sich wegen 2:
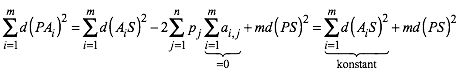 (5)
(5)
Wenn
dieser Ausdruck (5) konstant sein soll, muss ![]() konstant
sein. Das hei§t, der Punkt P liegt
auf einer n–1-Hypersphre mit
dem Mittelpunkt S. Dies war zu beweisen.
konstant
sein. Das hei§t, der Punkt P liegt
auf einer n–1-Hypersphre mit
dem Mittelpunkt S. Dies war zu beweisen.
Ein vorgegebener Wert k2 fr die Konstante (5) fhrt auf:
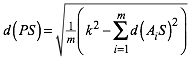 (6)
(6)
Die gesuchte Punktmenge H ist also eine n–1-Hypersphre um den Schwerpunkt S mit dem durch (6) gegebenen Radius.
Fr einen reellen Radius muss die Bedingung
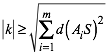 (7)
(7)
erfllt sein.
5 Beispiele
5.1 Vorbemerkung zur Visualisierung
Das algebraisch gemeinte Quadrat einer Strecke kann durch ein geometrisches Quadrat mit der Strecke als Seitenlnge visualisiert werden. Dem algebraischen Quadrat entspricht der Flcheninhalt des geometrischen Quadrates.
Diese Visualisierung kennen wir von der Pythagoras-Ikone (Abb. 1a) her.
Wenn wir es allerdings wie in (1) mit m Quadraten zu tun haben und m recht gro§ ist, fhrt dies in der geometrischen Visualisierung bald einmal zu berlappungen der Quadrate.
Im 3- oder hherdimensionalen Raum wirken die (zweidimensionalen) Quadrate wie quadratische Flatterfahnen an der Fahnenstange.
5.2 Pythagoras
Wir arbeiten mit einem rechtwinkligen Dreieck A1A2P mit dem rechten Winkel bei P. Nach dem Satz des Thales liegt P auf dem Kreis mit Durchmesser A1A2.
Wir setzen ![]() . Weiter ist m
= 2. Der Schwerpunkt S der beiden
Punkte A1 und A2 ist der Mittelpunkt der
Strecke A1A2. Daher ist
. Weiter ist m
= 2. Der Schwerpunkt S der beiden
Punkte A1 und A2 ist der Mittelpunkt der
Strecke A1A2. Daher ist ![]() . Weiter ist
. Weiter ist ![]() .
.
Fr die Summe (5) der Quadrate der Abstnde von P zu A1 und A2 erhalten wir:
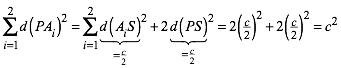 (8)
(8)
Das c2 setzt sich aus vier
Teilquadraten der Seitenlnge ![]() zusammen. Die
Abbildung 1 gibt zwei Visulisierungen des Satzes von Pythagoras. Die Abbildung
1a kennen wir von der Schule her. Die Abbildung 1b ist symmetrisch im Sinne
ãzwei rote Quadrate = zwei blaue QuadrateÒ.
zusammen. Die
Abbildung 1 gibt zwei Visulisierungen des Satzes von Pythagoras. Die Abbildung
1a kennen wir von der Schule her. Die Abbildung 1b ist symmetrisch im Sinne
ãzwei rote Quadrate = zwei blaue QuadrateÒ.
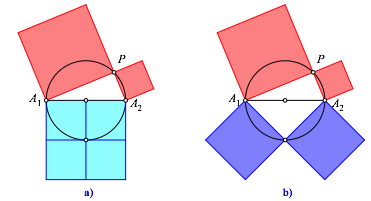
Abb.1: Pythagoras: Rot = blau
Die Abbildung 2 gibt den Link zwischen den beiden Darstellungsarten. Wegen der Invarianz der Quadratsumme knnen wir die beiden roten Quadrate durch zwei gleich gro§e, symmetrisch liegende dunkelblaue Quadrate ersetzen (Abb. 1b). Diese wiederum knnen wir durch je zwei hellblaue Quadrate ersetzen, welche zusammen das klassische c2 ergeben.
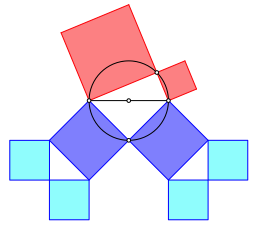
Abb. 2: Link zwischen hellblau und dunkelblau
5.3 Al-Sijzi
Wir
arbeiten mit einem beliebigen Dreieck A1A2P. Wir setzen wiederum ![]() . Weiter ist m
= 2 und der Schwerpunkt S der beiden
Punkte A1 und A2 der Mittelpunkt der
Strecke A1A2. Daher ist
. Weiter ist m
= 2 und der Schwerpunkt S der beiden
Punkte A1 und A2 der Mittelpunkt der
Strecke A1A2. Daher ist ![]() . Wir zeichnen einen Kreis um S und bewegen den Punkt P
darauf. Es ist also
. Wir zeichnen einen Kreis um S und bewegen den Punkt P
darauf. Es ist also ![]() konstant
(die von P ausgehende Schwerlinie). Aus
(5) erhalten wir:
konstant
(die von P ausgehende Schwerlinie). Aus
(5) erhalten wir:
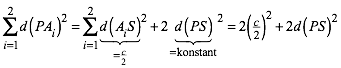 (9)
(9)
Die Abbildungen 3 und 4 illustrieren den Sachverhalt.
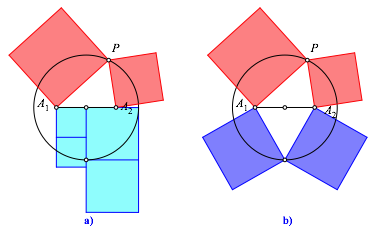
Abb. 3: Al-Sijzi: Rot = blau
Die
Flchensumme der roten Quadrate ist invariant bei einer Bewegung von P auf dem Kreis um S. Diese Flchensumme ist wegen (9) gleich der Flchensumme von
zwei Quadraten der Seitenlnge ![]() plus der
Flchensumme von zwei Quadraten mit dem Kreisradius als Seitenlnge (Abb. 3a).
Wegen der Invarianz der Quadratsumme knnen wir die beiden roten Quadrate durch
zwei gleich gro§e, symmetrisch liegende dunkelblaue Quadrate ersetzen (Abb.
3b). Die Abbildung 4 gibt den Link zwischen den hellblauen und den dunkelblauen
Quadraten.
plus der
Flchensumme von zwei Quadraten mit dem Kreisradius als Seitenlnge (Abb. 3a).
Wegen der Invarianz der Quadratsumme knnen wir die beiden roten Quadrate durch
zwei gleich gro§e, symmetrisch liegende dunkelblaue Quadrate ersetzen (Abb.
3b). Die Abbildung 4 gibt den Link zwischen den hellblauen und den dunkelblauen
Quadraten.
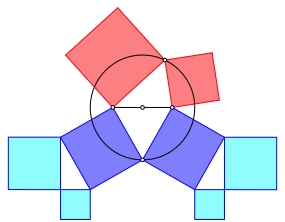
Abb. 4: Link zwischen hellblau und dunkelblau
5.4 Drei Punkte
Das einfachste ebene Beispiel, das ber die Stze des Pythagoras und des Sijzi hinausgeht, besteht aus drei Punkten A1, A2, A3 (Abb. 5). Die drei Quadrate, die der Visualisierung der drei Abstandsquadrate dienen, berlappen sich teilweise. Der Punkt P kurvt auf einem Kreis um den Schwerpunkt S. Die Summe der Quadrate der Abstnde bleibt invariant.
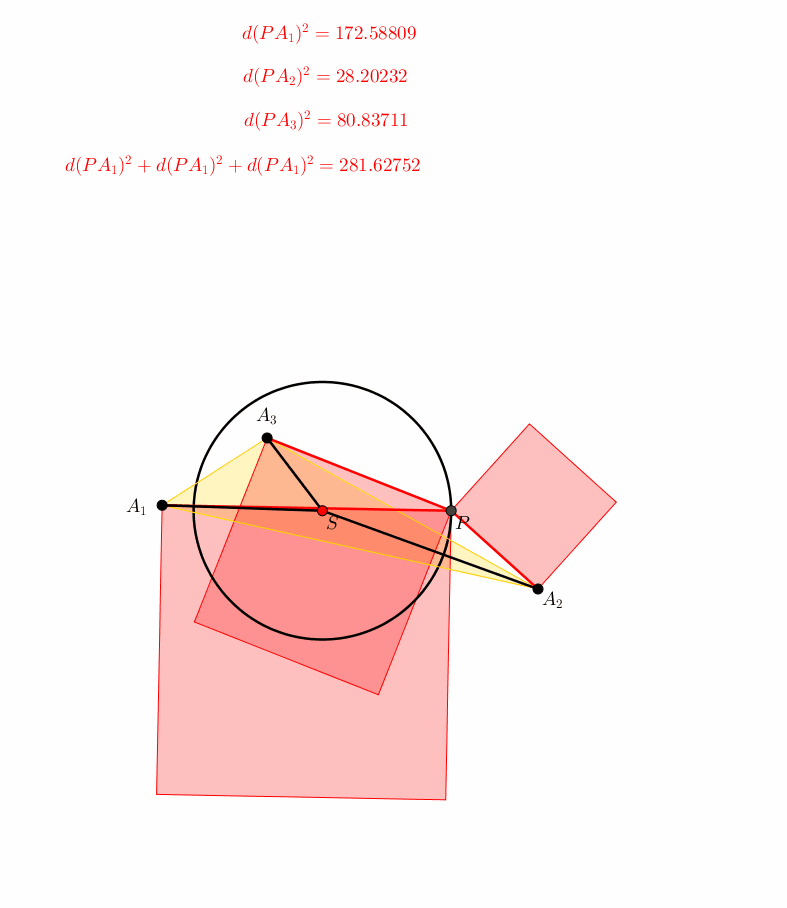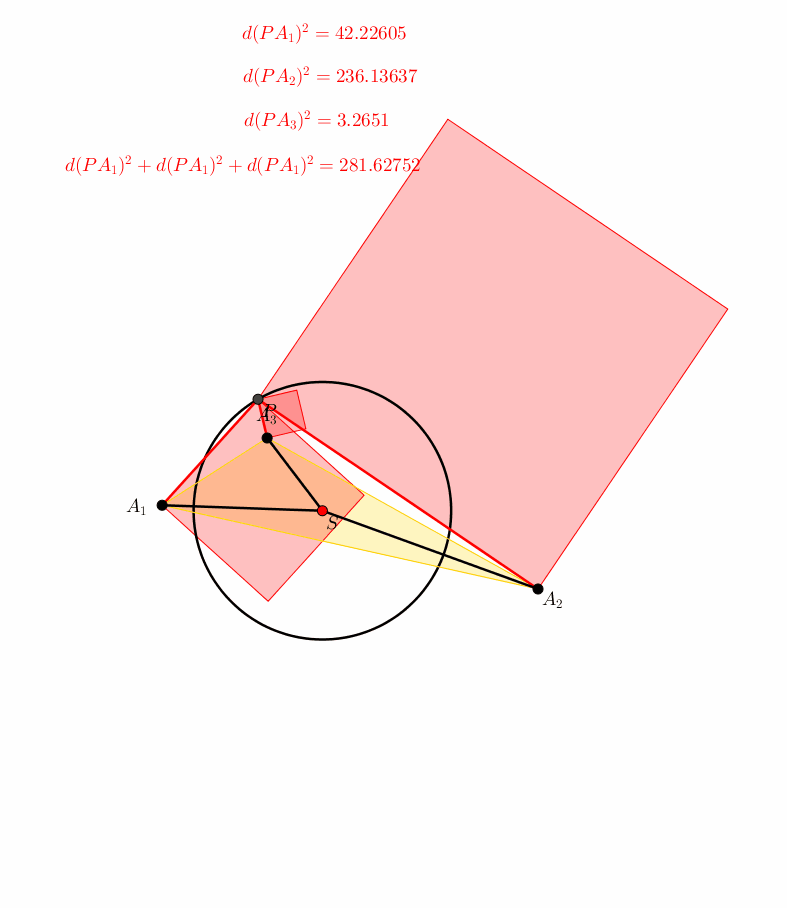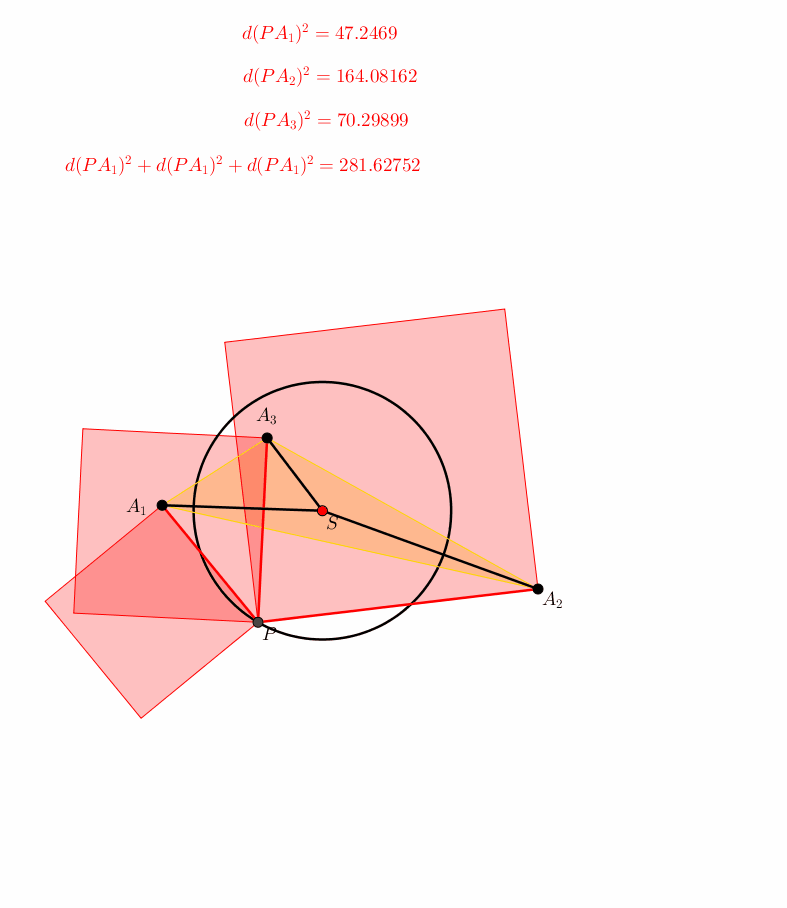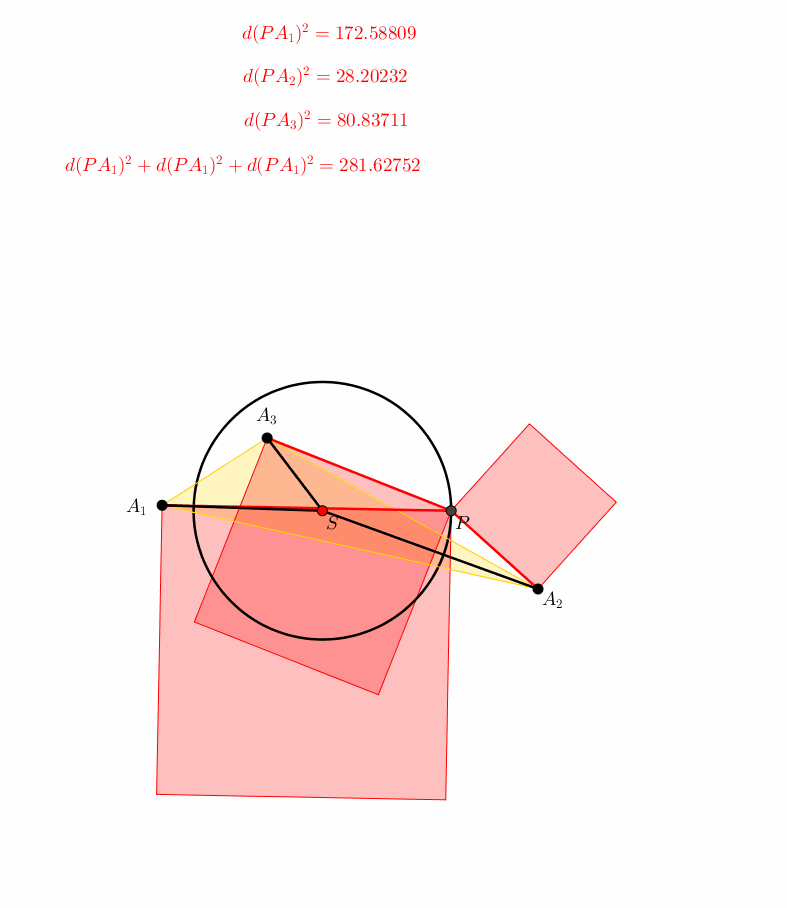
Abb. 5: Drei Punkte
6 Die kopernikanische Wende
In der Abbildung 5 kreist der Punkt P um die Figur mit den drei Punkten A1, A2, A3 wie die Sonne um die Erde.
Wir knnen die Sichtweise umkehren. Wir halten den Punkt P fest und drehen die Figur mit den drei Punkten A1, A2, A3 um ihren Schwerpunkt (Abb. 6). Die Summe der Abstandsquadrate bleibt invariant.
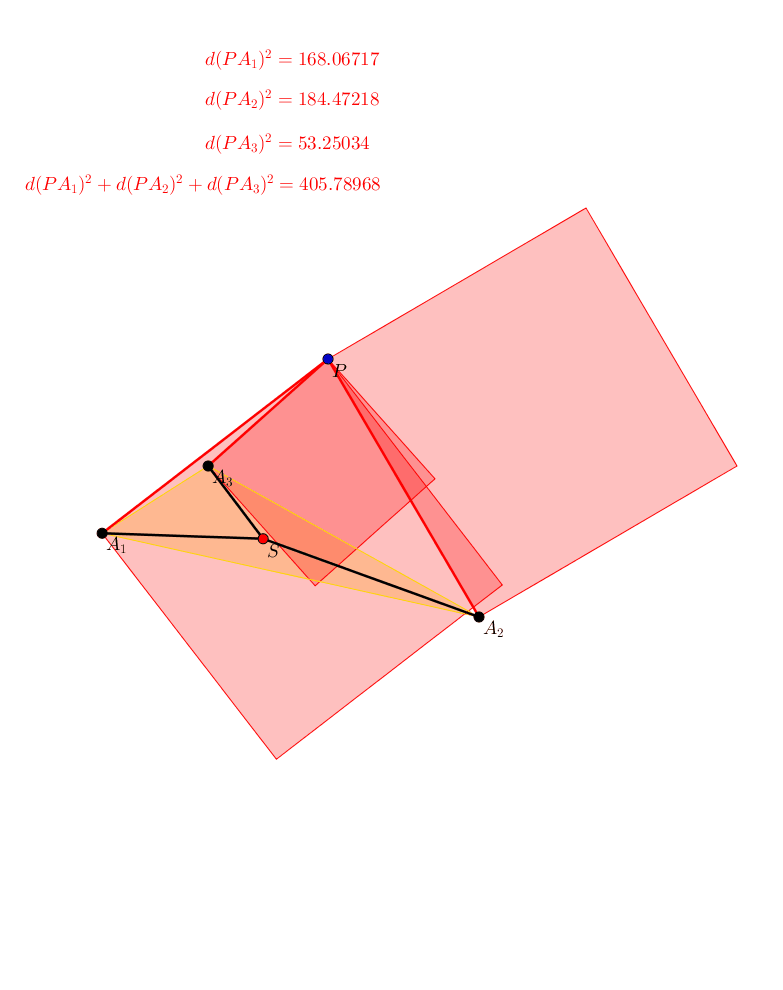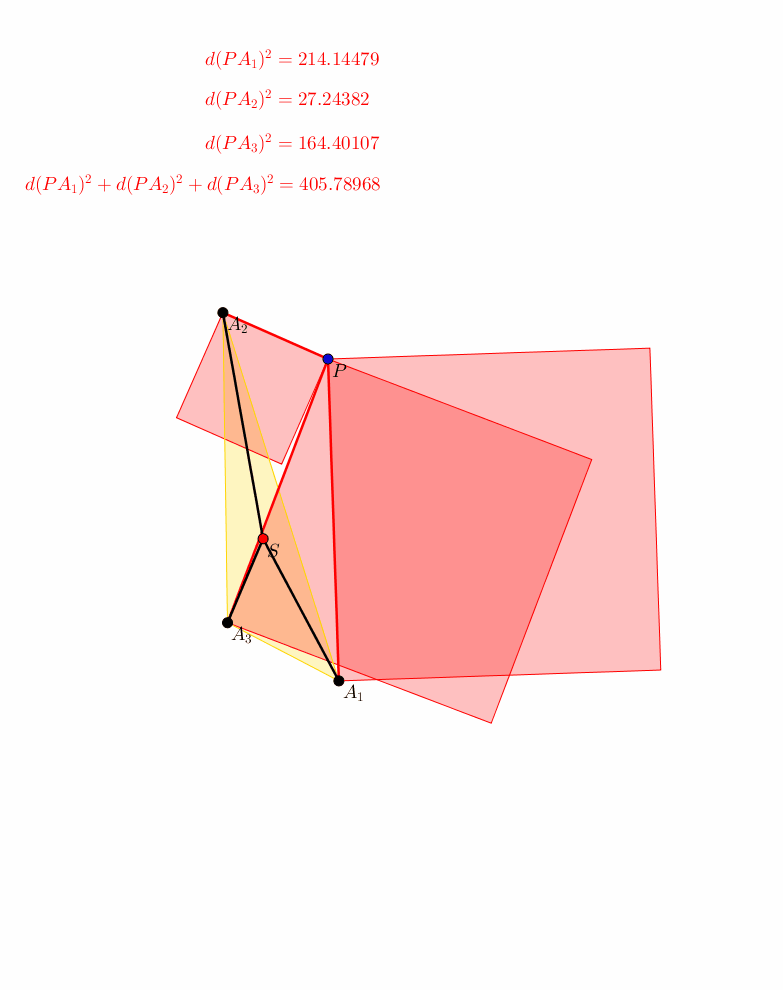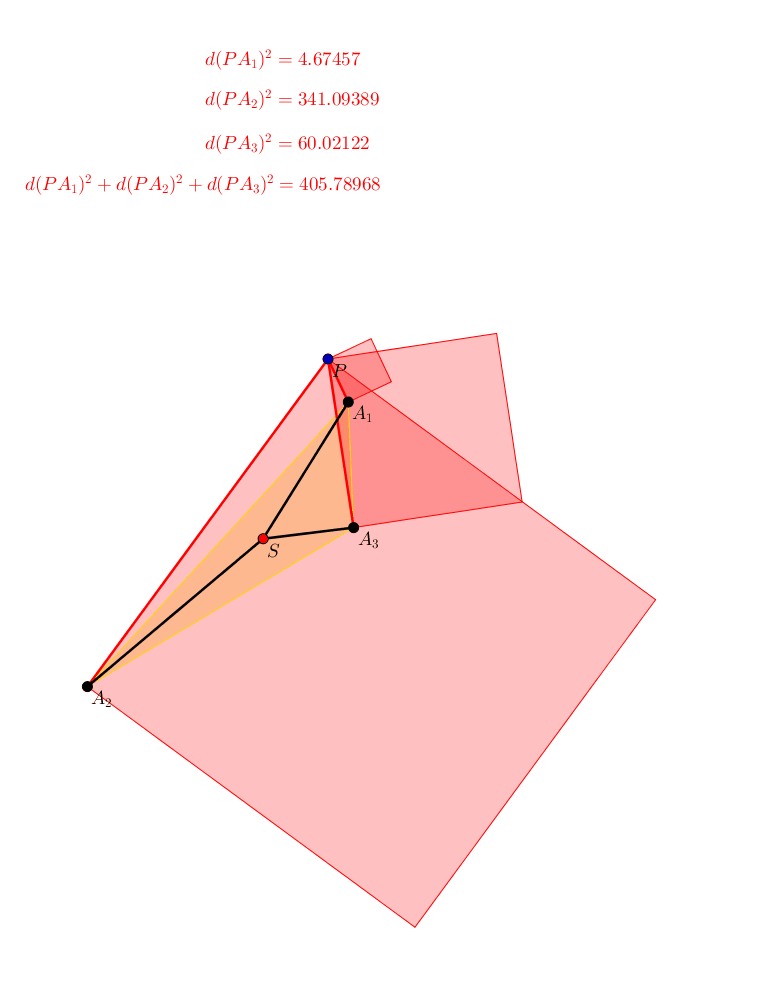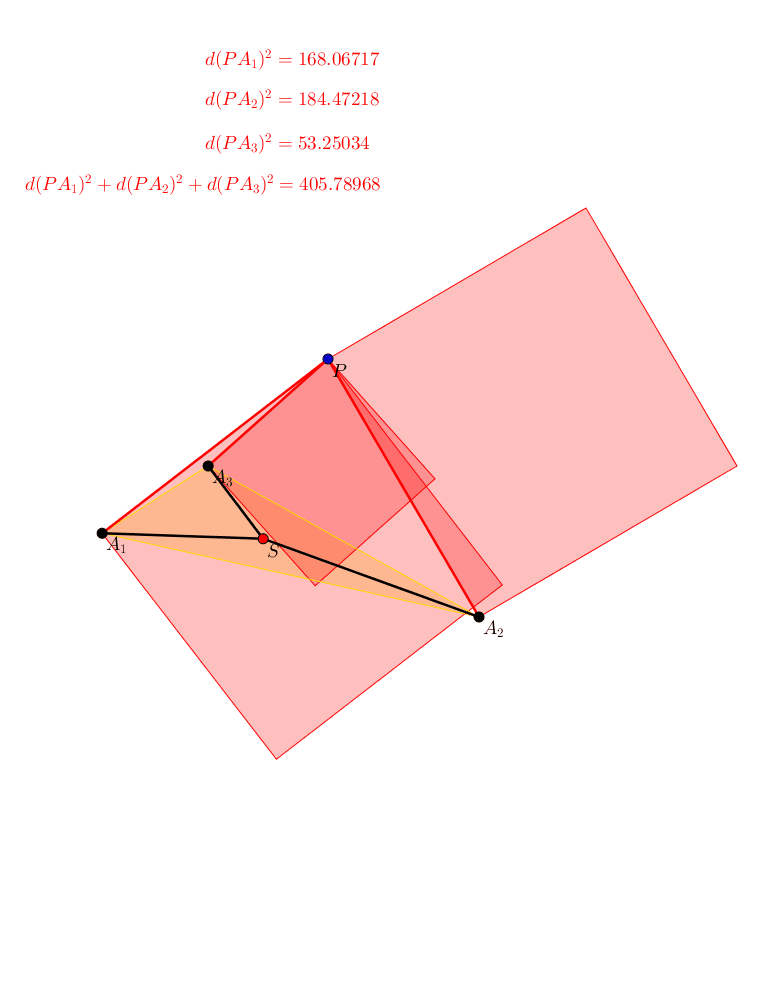
Abb. 6: Umkehrung der Sichtweise
Die Abbildung 7 zeigt ein Beispiel mit hoher Symmetrie. Der Radius des 5-Sternes ist 1, der Abstand des Punktes P von S ist 3. Aus (5) erhalten wir:
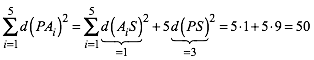 (10)
(10)
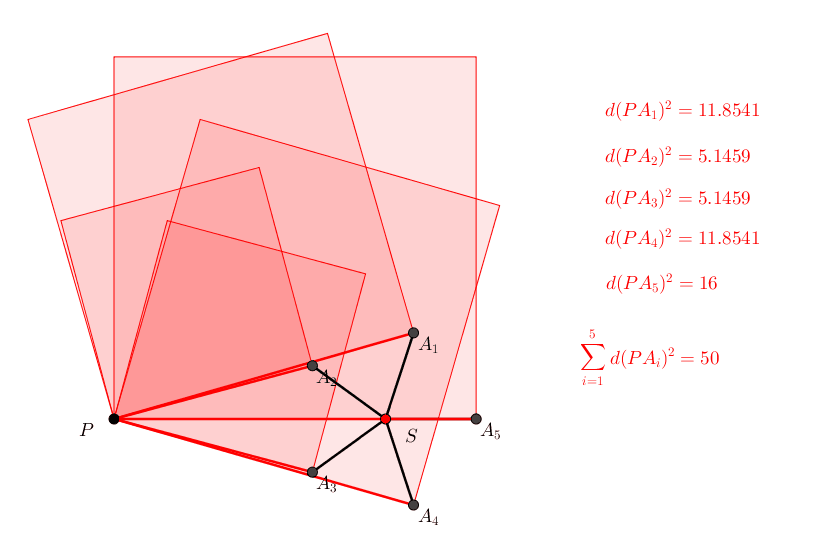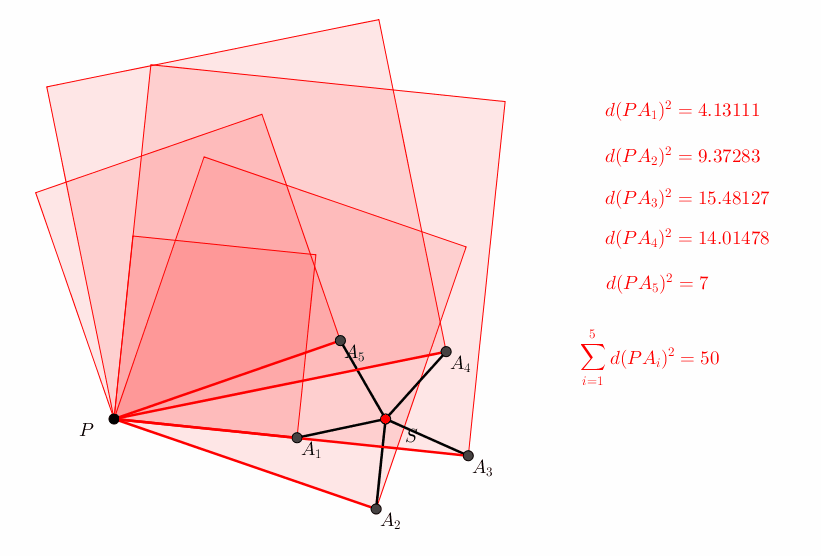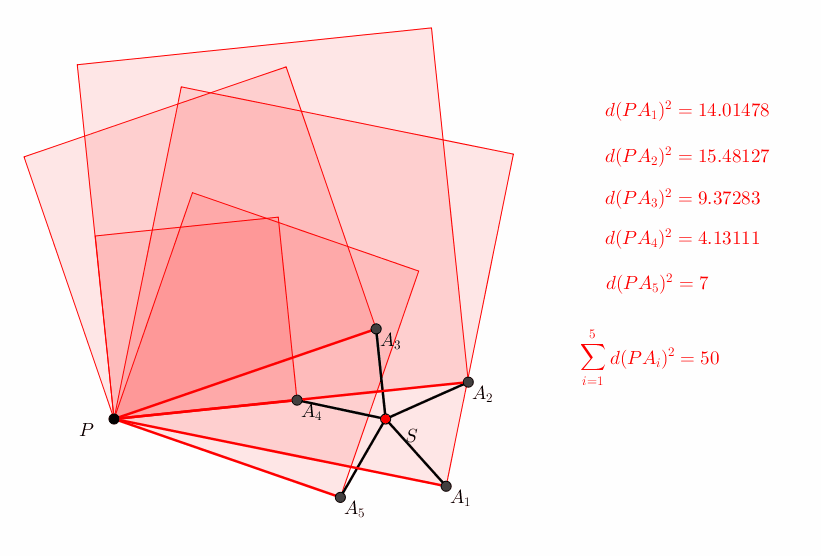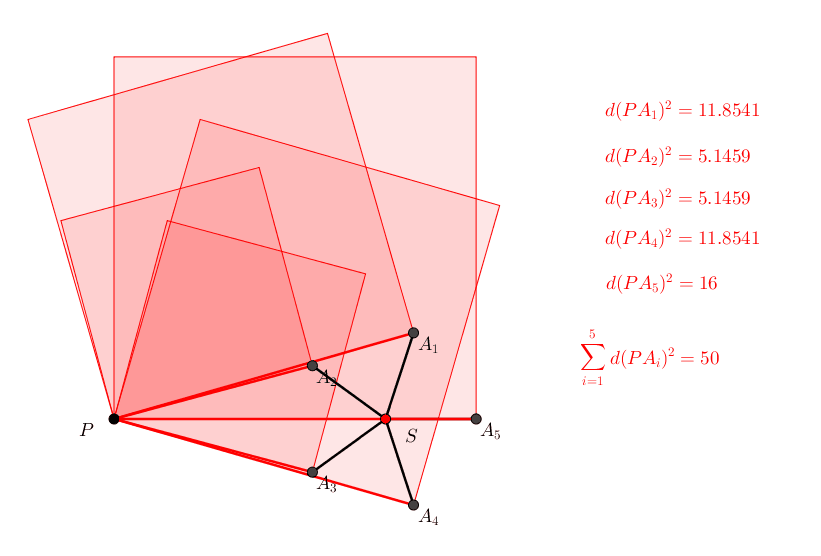
Abb. 7: Kinematik
Man beachte, dass die fnf Quadratecken rechts oben in jeder Position ein regelm§iges Fnfeck bilden. Ebenso die Ecken links oben.
7 Rechenbeispiele
7.1 Regelm§iges Vieleck
Dem Einheitskreis wird ein regelm§iges m-Eck einbeschrieben. Weiter whlen wir einen beliebigen Punkt P auf dem Einheitskreis. Wie gro§ ist die Summe der Quadrate der Abstnde von P zu den Ecken des m-Ecks?
Man kann die Aufgabe zunchst exemplarisch und dann allgemein mit Trigonometrie durchexerzieren (der Autor hat beides gemacht). Man lernt dabei einiges.
Das Ergebnis ist 2m. Dies folgt unmittelbar aus (5).
7.2 Regelm§iges Polyeder
Der Einheitskugel wird ein regelm§iges Polyeder (platonischer Krper) einbeschrieben. Weiter whlen wir einen beliebigen Punkt P auf der Einheitskugel. Wie gro§ ist die Summe der Quadrate der Abstnde von P zu den Ecken des Polyeders?
Das Ergebnis ist zweimal die Eckenzahl. Beim Wrfel also 8.
8 Gewichtung
Wir knnen die einzelnen Abstandsquadrate unterschiedlich gewichten. Damit die Summe invariant bleibt, mssen die Punkte A1, ... , Am bei der Schwerpunktbestimmung entsprechend gewichtet werden. Die Punktmenge H ist dann wieder eine n–1-Hypersphre um S.
In der Abbildung 8 ist der Punkt A2 gegenber dem Punkt A1 doppelt gewichtet.
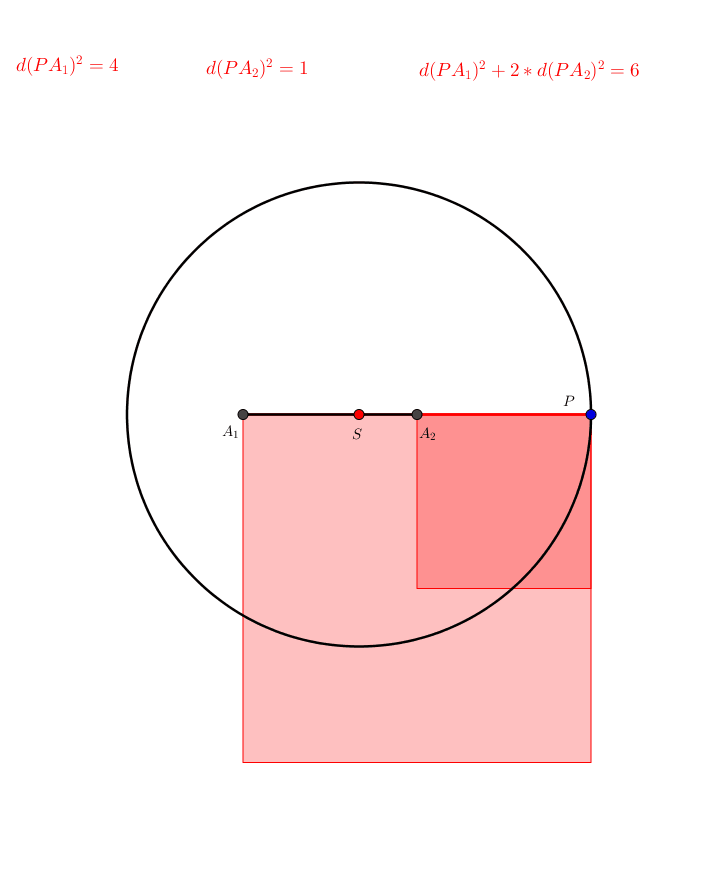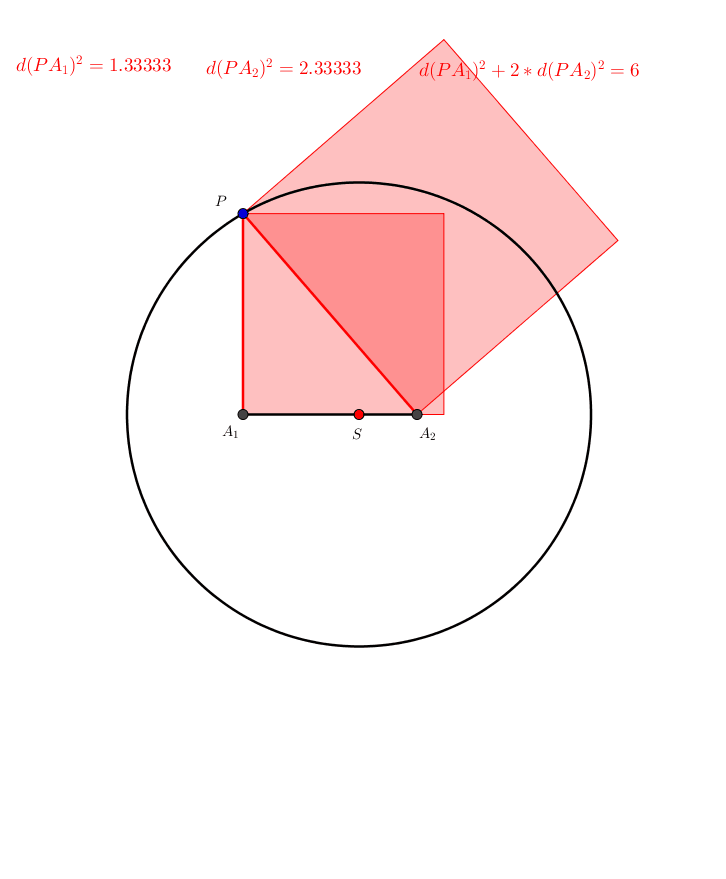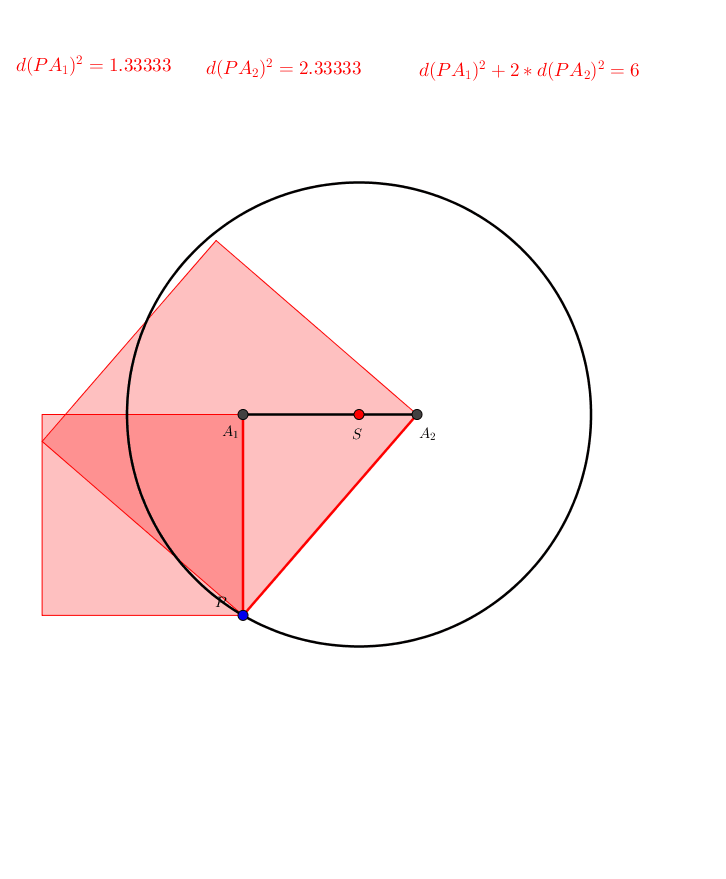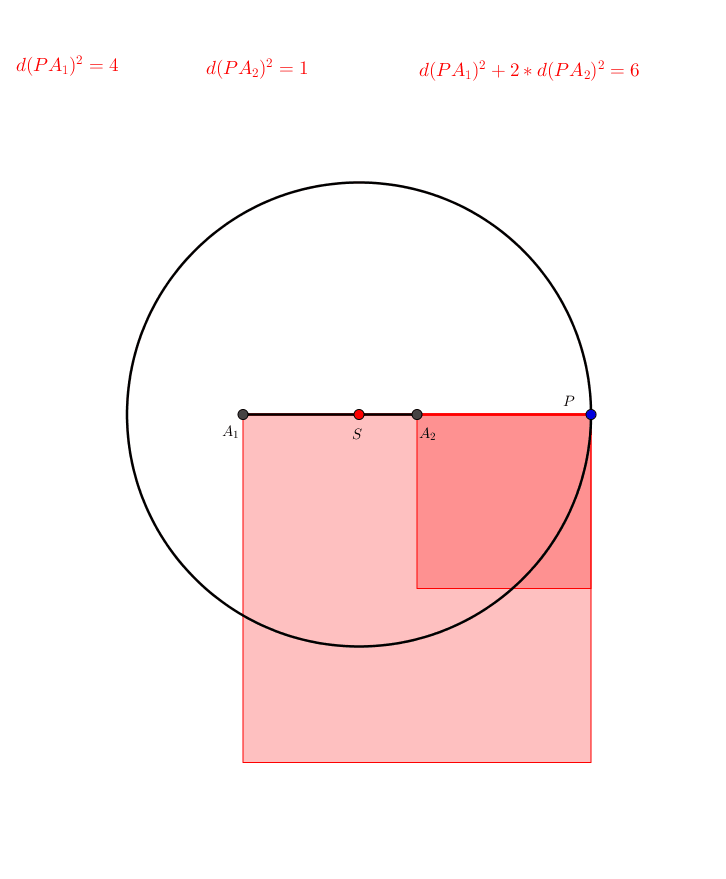
Abb. 8: Ungleiche Gewichtung
9 Link mit Statistik
Den
Begriffen Schwerpunkt und Summe der Abstandsquadrate vom Schwerpunkt
entsprechen in der Statistik die Begriffe Mittelwert
und Streuung.
10 Verallgemeinerung oder Sonderfall?
Der Satz des Pythagoras ist im Satz des al-Sijzi und in der Formel (5) als Sonderfall enthalten. Ebenso ist der Satz des al-Sijzi in der Formel (5) als Sonderfall enthalten.
Es wre nun aber falsch, aus der Formel (5) einen Beweis fr den Satz des Pythagoras oder den Satz des al-Sijzi abzuleiten. Wir haben nmlich bei der Herleitung von (5) den Satz des Pythagoras in (3) eingesetzt.
Die korrekte Formulierung ist wohl, dass man den Satz des Pythagoras, den Satz des al-Sijzi und die Formel (5) als quivalent bezeichnet.
Websites
Hans
Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi/index.html
Hans
Walser: Al-Sijizi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi2/Al-Sijzi2.htm
Hans
Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi3/Al-Sijzi3.htm
Hans
Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi4/Al-Sijzi4.htm