Hans Walser, [20210106]

Al-Sijzi

1 Worum geht es?

Kinematische Beispiele

2 Pythagoras und al-Sijzi

Nach dem Satz des Pythagoras bleibt beim rechtwinkligen Dreieck die Summe der Quadratflächen über den beiden Katheten invariant, wenn der Eckpunkt beim rechten Winkel auf dem Thaleskreis bewegt wird.

In einem beliebigen Dreieck ABC bleibt die Summe a² + b² invariante, wenn die Ecke C auf dem Kreis um den Mittelpunkt der Strecke AB und dem Radius s_c (von C ausgehende Schwerlinie) bewegt wird (Satz von al-Sijzi). Alternativ können wir auch s_c festlassen und die Strecke AB um ihren Mittelpunkt drehen (Abb. 1).

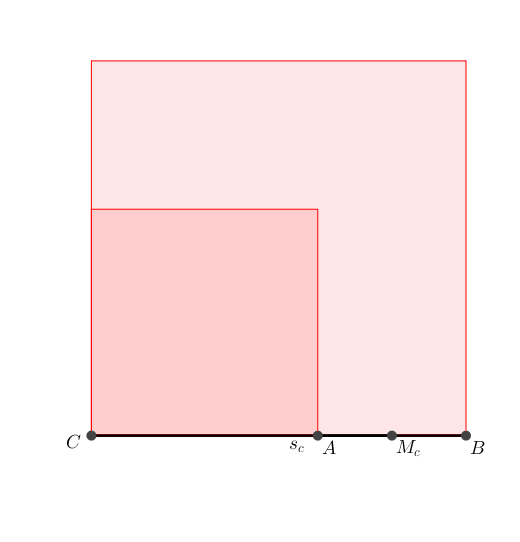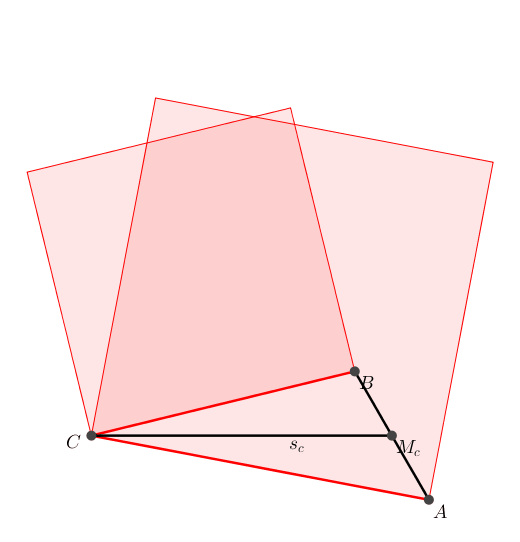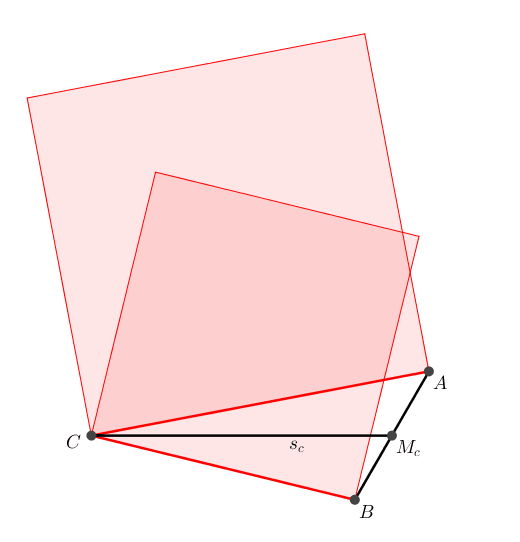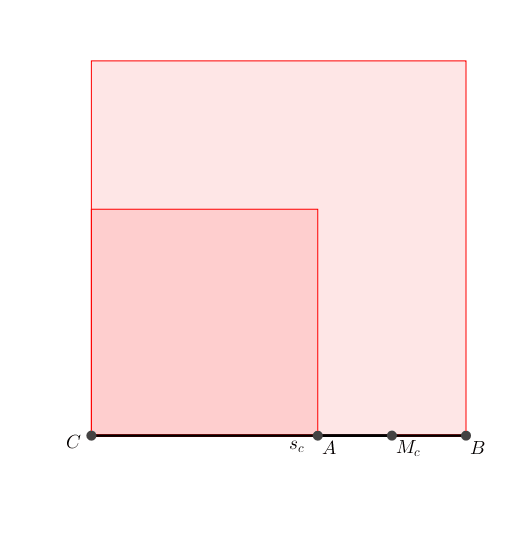
Abb. 1: Propeller. Invariante Quadratflächensumme

Es funktioniert auch mit einem dreiteiligen (oder n-teiligen) Propeller (Abb. 2).

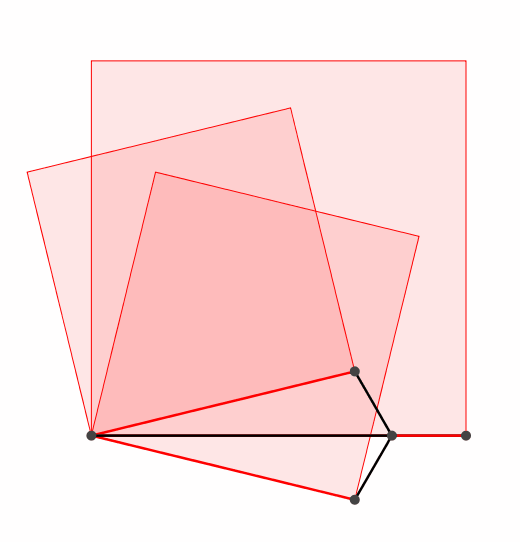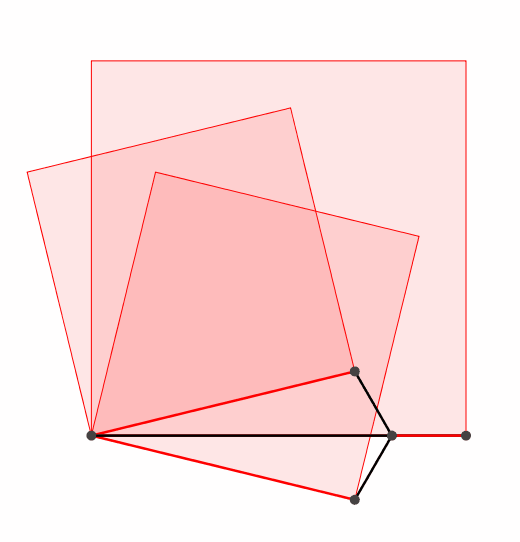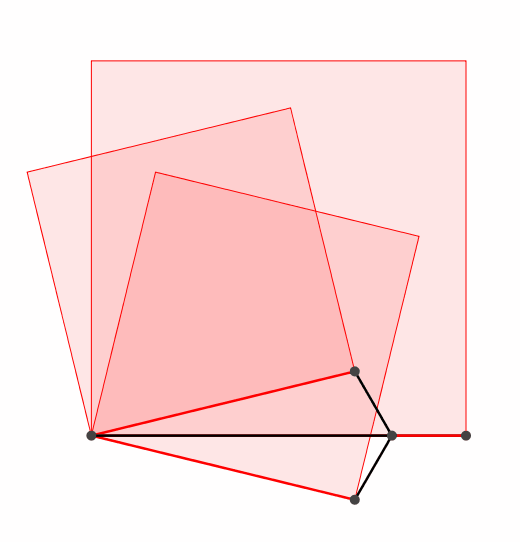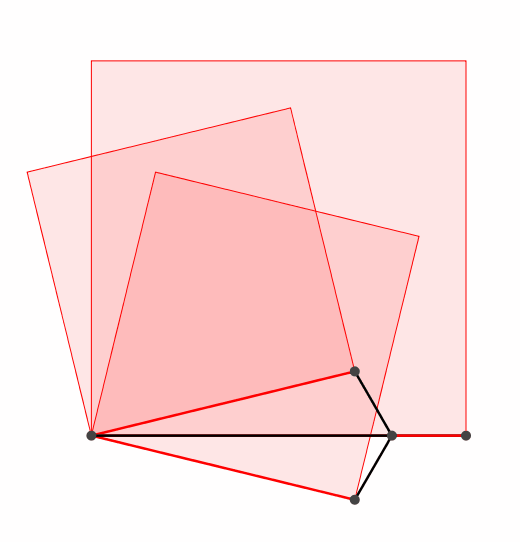
Abb. 2: Dreiteiliger Propeller

3 Noch mehr Kinematik

Wir lassen zwei Propeller synchron, aber phasenversetzt rotieren.

Die Flächensumme der angesetzten Quadrate ist invariant (Abb. 3).

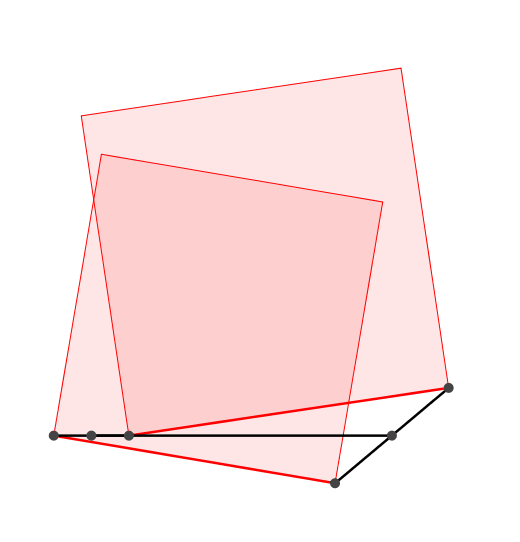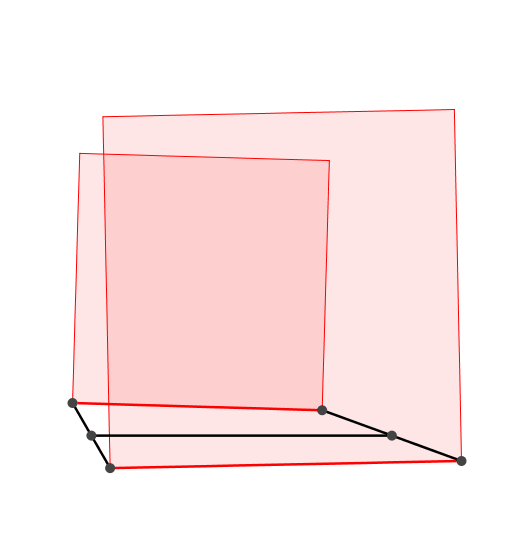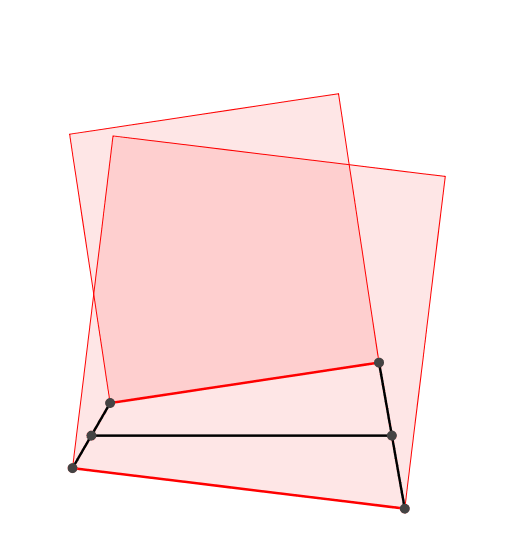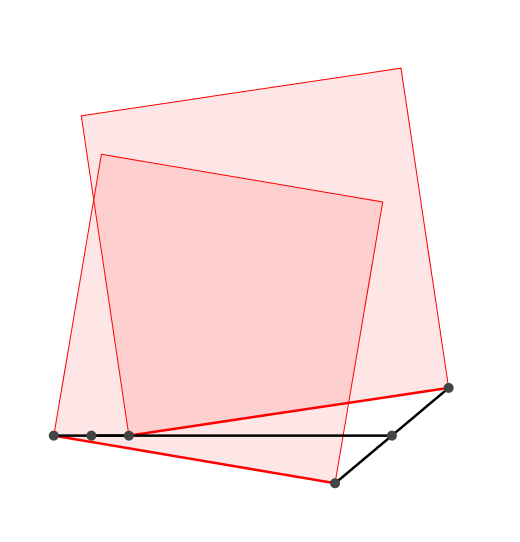
Abb. 3: Zwei Propeller

Beweis: Wir bezeichnen die Radien der beiden Propeller mit a beziehungsweise b. Im Standbild der Abbildung 4 ist nur eines der beiden Quadrate eingezeichnet, die folgende Überlegung gilt aber auch für das andere Quadrat.

Wir verschieben das Quadrat (rot) so, dass eine Ecke in das Drehzentrum des ersten Propellers zu liegen kommt. Der Verschiebungsvektor hat die Länge a. Das verschobene Quadrat ist grün gezeichnet. Der violett eingezeichnete Winkel ist die Phasenversetzung.

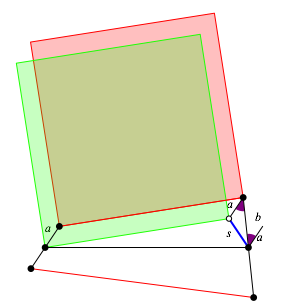
Abb. 4: Verschieben eines Quadrates

Das grüne Quadrat hat nun die linke untere Ecke fest. Die rechte untere Ecke rotiert mit dem Propellerarm s. Dieser lässt sich aus a und b sowie der Phasenversetzung berechnen.

Das grüne Quadrat ist also in der Situation der Abbildung 1.

Entsprechend kann das andere rote Quadrat verschoben werden. Aus dem Satz von al-Sijzi gemäß Abbildung 1 folgt daher die Invarianz der Flächensumme der Abbildung 3.

4 Vier Propeller

Wir können in die beiden rechten oberen Quadratecken der Abbildung 3 und ebenso in die beiden linken oberen Ecken je einen weiteren Propeller einpassen (Abb. 5).

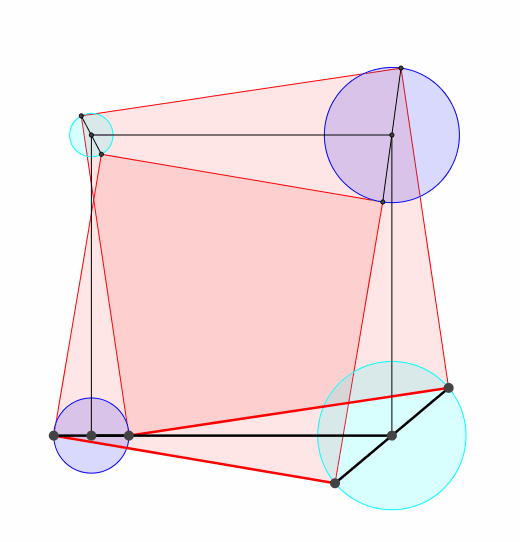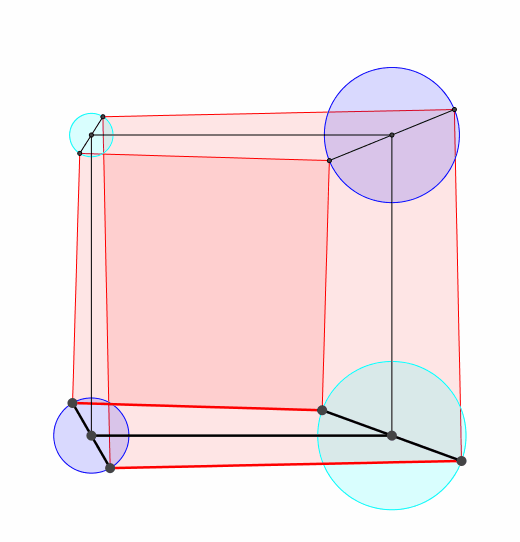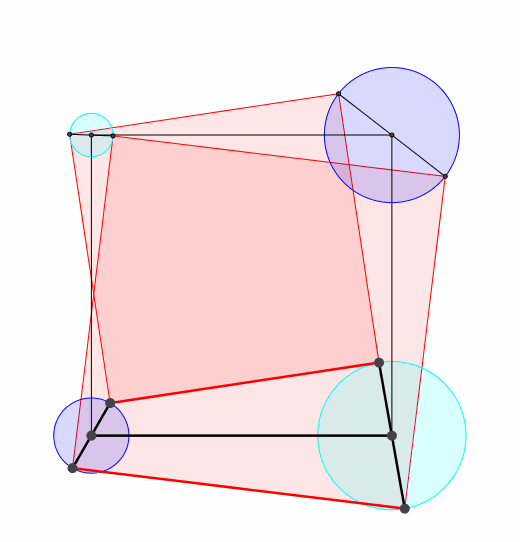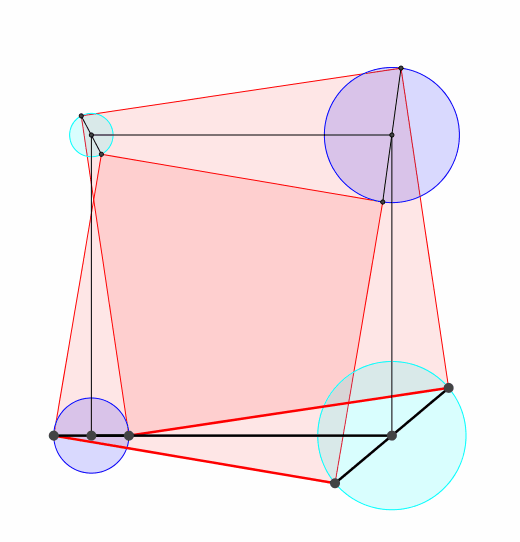
Abb. 5: Zwei weitere Propeller

Somit haben wir nun vier Propeller. Ihre Drehzentren bilden ein Quadrat. Für die zu den Propellern gehörenden Drehkreise gilt: Die alternierende Summe der Kreisflächen ist null. Es ist also dunkelblau = hellblau.

Um dies einzusehen ergänzen wir zunächst die Abbildung 4 durch die beiden neuen Zentren (Abb. 6). Die Radien der beiden zusätzlichen Propeller bezeichnen wir mit c beziehungsweise d.

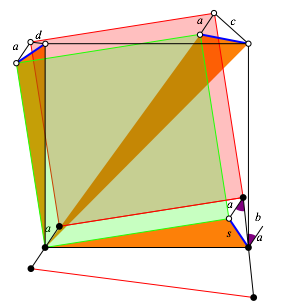
Abb. 6: Die vier Drehzentren

Die blauen Strecken der Abbildung 6 lassen sich zu einem Quadrat zusammenfügen (Abb. 7a). Ein dieses Quadrat passen auch die vier Radien a, b, c und d. Dies wird durch die Abbildung 7b illustriert.

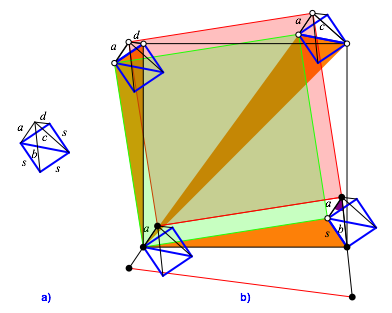
Abb. 7: Kleines Quadrat mit Radien

Aus der Figur 7a lässt sich eine Beziehung für die vier Radien herleiten. Wir arbeiten mit den Bezeichnungen der Abbildung 8b.

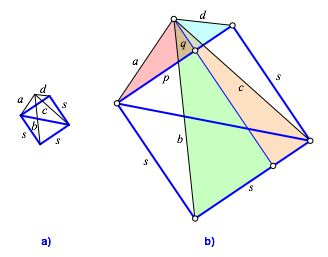
Abb. 8: Radien und Quadrat

Für die Quadrate der Radien ergibt sich mit dem Satz des Pythagoras:

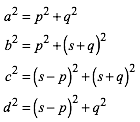(1)

Daraus ergibt sich, dass die alternierende Summe der Quadrate der Radien verschwindet:

(2)

Damit verschwindet aber auch die alternierende Summe der Kreisflächen in der Abbildung 5.

5 Weitere Beispiele

Die Summe der fünf roten Quadratflächen (Abb. 9) ist invariant. Die alternierende Summe der vier Fünfeckflächen ist null.

Abb. 9: Quadrate und Fünfecke

Die Summe der drei roten Dreiecksflächen (Abb. 10) ist invariant.

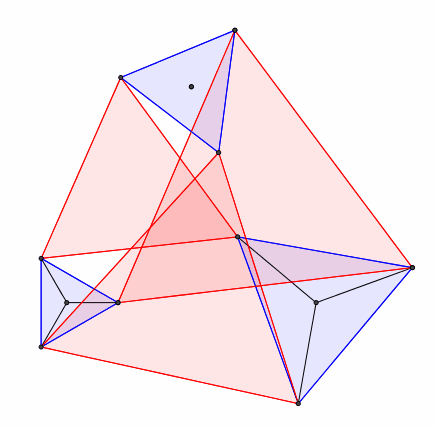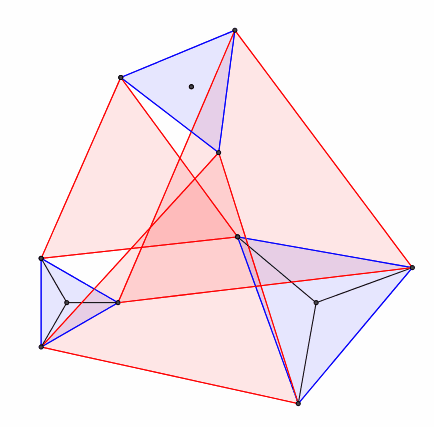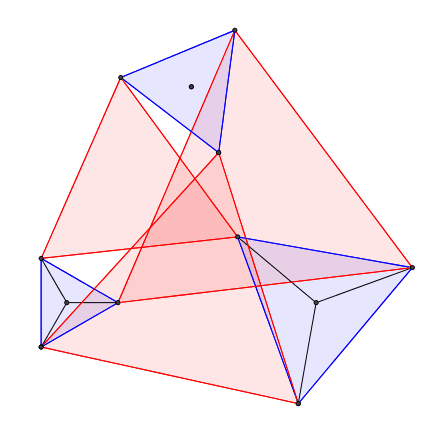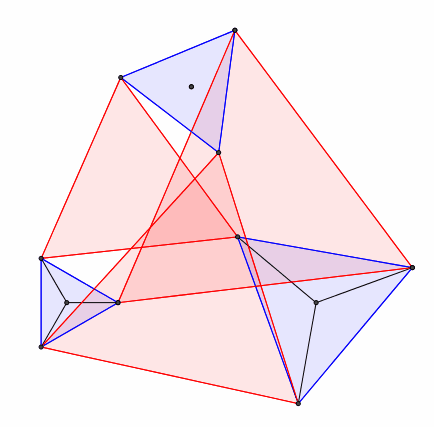
Abb. 10: Dreiecke und Dreiecke

Websites

Hans Walser: Al-Sijizi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi2/Al-Sijzi2.htm

Hans Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi/index.html

Hans Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi3/Al-Sijzi3.htm

Hans Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi4/Al-Sijzi4.htm

Hans Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi5/Al-Sijzi5.htm

Hans Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi7/Al-Sijzi7.htm

Hans Walser: Alternierende Quadratsummen
http://www.walser-h-m.ch/hans/Miniaturen/A/Alternierende_Quadratsummen/Alternierende_Quadratsummen.htm

Hans Walser: Alternierende Summe von Abstandsquadraten
http://www.walser-h-m.ch/hans/Miniaturen/A/Alternierende/Alternierende.htm