Hans Walser, [20210107]

Al-Sijzi

1 Worum geht es?

Beweis des Satzes von al-Sijzi mit dem Kosinussatz

2 Herleitung

Wir berechnen in einem beliebigen Dreieck ABC (Abb. 1a) die Quadratsumme a² + b².

Abb. 1: Dreieck

Im Dreieck CM_cB (Abb. 1b) erhalten wir mit dem Kosinussatz:

(1)

Im Nachbardreieck AM_cC ergibt sich analog:

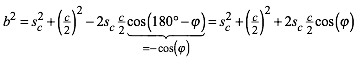(2)

Bei der Addition von (1) und (2) fällt der Kosinus-Anteil heraus:

(3)

Die Formel (3) ist die formelmäßige Formulierung des Satzes von Sijzi.

Die Abbildung 2 illustriert den Sachverhalt.

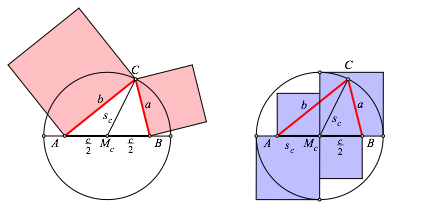
Abb. 2: Al-Sijzi: Rot = blau

Der Witz der Sache ist, dass der Winkel in (3) nicht vorkommt. Wenn wir ihn verändern, bleibt die Quadratsumme a² + b² invariant. Das sieht man auch bei den blauen Flächen in der Abbildung 2.

3 Zwei Sichtweisen

Wir können die Veränderung des Winkels auf verschiedene Weisen handhaben.

Wir können die Grundseite AB festhalten und die dritte Ecke auf dem Kreis um M_c mit Radius s_c bewegen (Abb. 3).

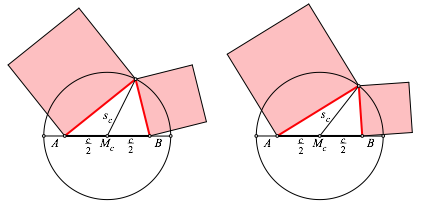
Abb. 3: Invariante Quadratsumme

Wir können aber auch die Schwerlinie s_c festhalten und die Grundseite um M_c drehen (Abb. 4 und 5).

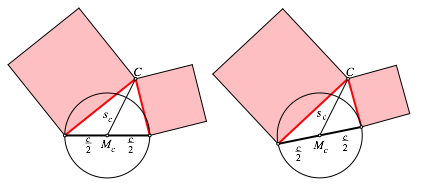
Abb. 4: Invariante Quadratsumme

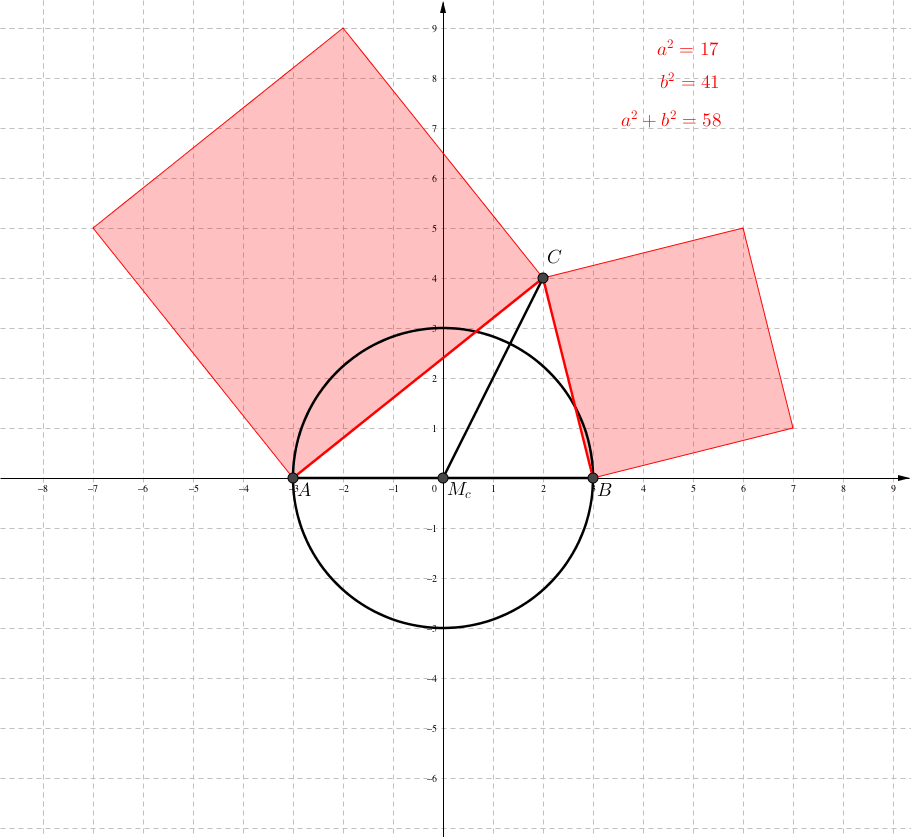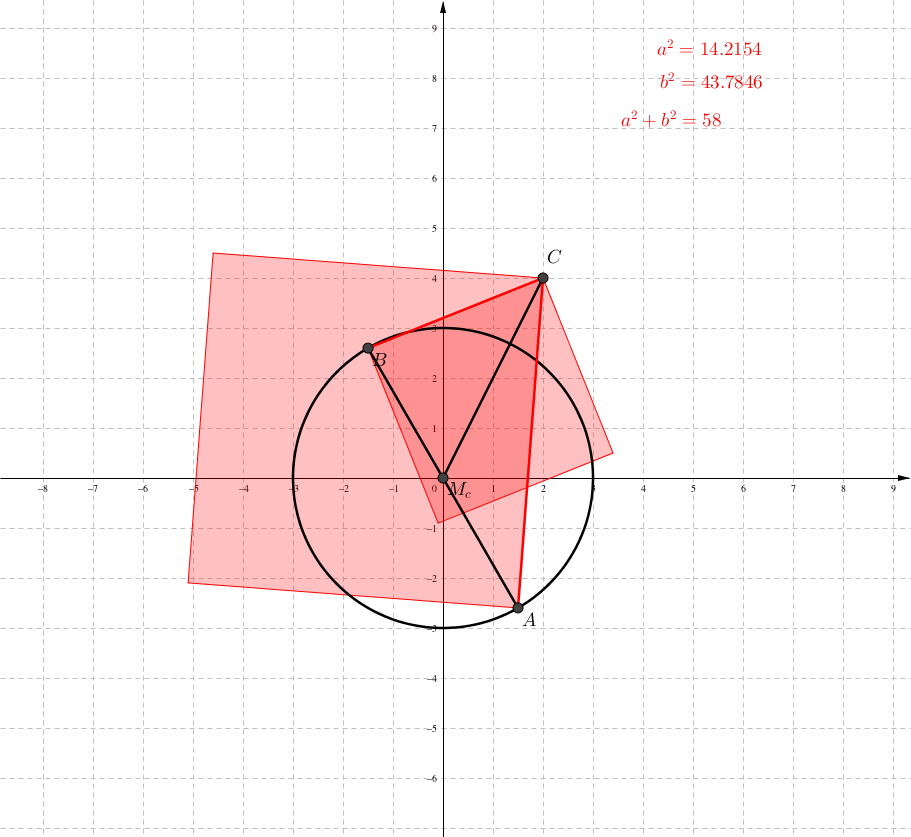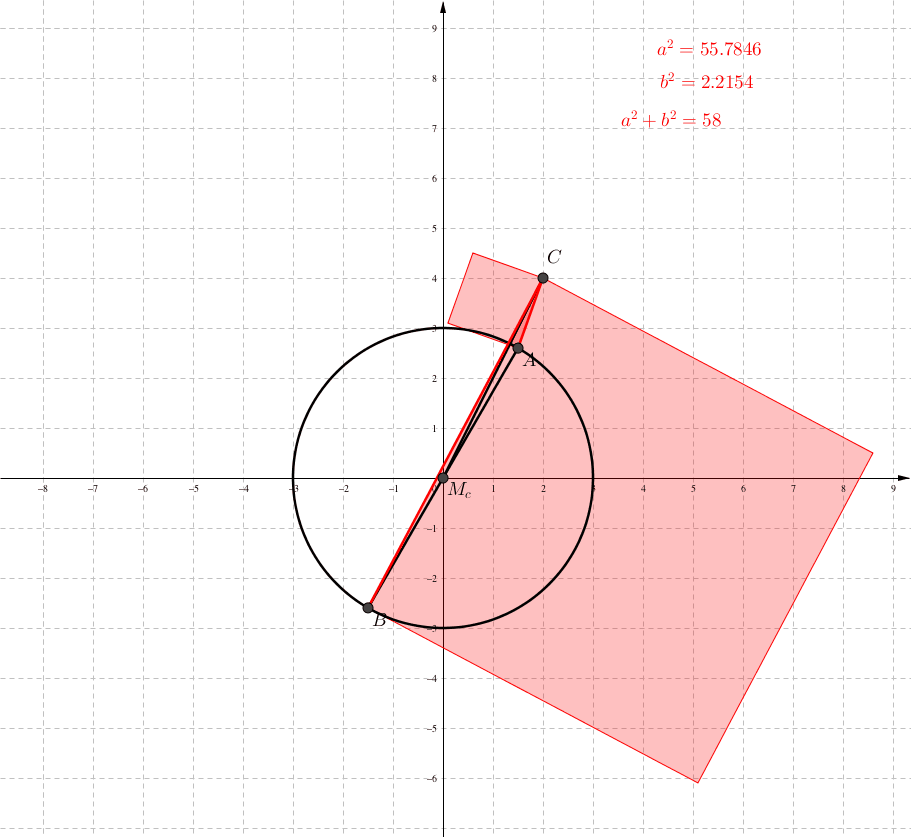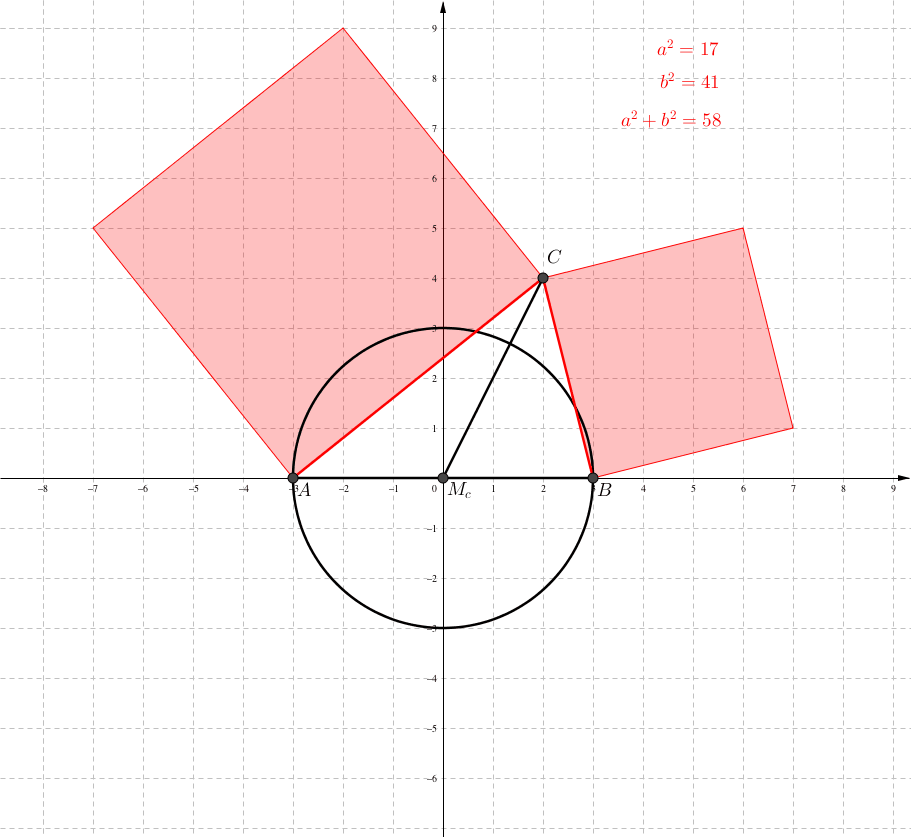
Abb. 5: Propeller

Websites

Hans Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi/index.html

Hans Walser: Al-Sijizi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi2/Al-Sijzi2.htm

Hans Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi3/Al-Sijzi3.htm

Hans Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi4/Al-Sijzi4.htm

Hans Walser: Al-Sijzi
http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi5/Al-Sijzi5.htm