Hans Walser, [20180119]

Alexander der Große und Pythagoras

Anregung: Chr. S., H.

1 Worum geht es?

Aus 4 Einzelquadraten können wir ein -Quadrat zusammenfügen (Abb. 1a) und analog aus 9 Einzelquadraten ein -Quadrat (Abb. 1b).

Lassen sich diese beiden Quadrate addieren im Sinne, dass ein neues Quadrat aus Einzelquadraten entsteht?

Abb. 1: Die beiden Quadrate

2 Schule

In Unterricht haben Schülerinnen und Schüler in der Reihenfolge a) bis g)

a) zu merken, dass es nicht geht

b) zu erforschen, ob es allenfalls mit anderen Zahlen geht

c) das Lehrerdreieck mit den Katheten 3 und 4 zu entdecken

d) das Dreieck mit den Katheten 5 und 12 zu entdecken

e) den semantischen Begriff des pythagoreischen Tripels zu erarbeiten

f) als Sternstunde eine Parametrisierung der pythagoreischen Tripel zu finden

g) als besondere Sternstunde zu zeigen, dass diese Parametrisierung alle pythagoreischen Tripel liefert

So steht es im Curriculum.

3 Wie es doch geht

Wir malen fünf Einzelquadrate rot an (Abb. 2a).

Und nun verfahren wir wie Alexander der Große vor dem gordischen Knoten. Wir zerschneiden. Zwar nicht mit dem Schwert, sondern zivilisiert mit der Schere.

Vier Einzelquadrate zerschneiden wir gemäß Abbildung 2b. Die orange Binneneinteilung (Halbieren und Dritteln) dient dazu, die Schnittlinie festzulegen.

Die verbleibenden vier Einzelquadrate zerschneiden wir gemäß Abbildung 2c.

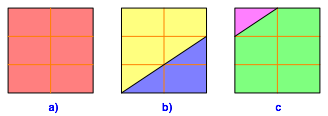
Abb. 2: Zerschneiden

Die Abbildung 3 zeigt eine Auslegeordnung unserer 13 Einzelquadrate.

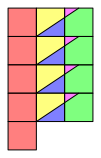
Abb. 3: Auslegeordnung

Nun können wir die Einzelteile zu einem Quadrat arrangieren (Abb. 4).

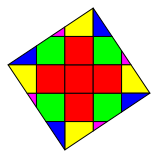
Abb. 4: Summenquadrat

Zugegeben, es handelt sich um einen alten Hut (Abb. 5).

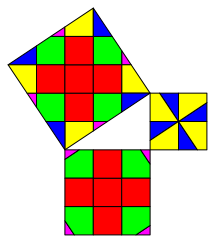
Abb. 5: Alter Hut

4 Die kleine Schwester des Pythagoras

Wie viele unzerschnittene rote Einzelquadrate gibt es im allgemeinen Fall?

Nun wird’s formal: Seien a und b natürliche Zahlen mit . Die Abbildung 6 zeigt im Quadratraster das zugehörige Rechteck für den Fall und . Wie viele Einzelquadrate werden von der eingezeichneten Diagonale zerschnitten?

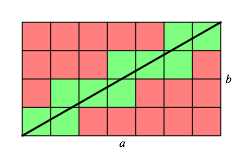
Abb. 6: Diagonale im Rasterrechteck

Von links nach rechts zählen wir mal a Positionen mit Einzelquadraten. An Stellen (Zaunpfahlproblem) sind zwei zerschnittene Einzelquadrate gestapelt. Somit haben wir insgesamt zerschnittene Einzelquadrate. Für die rote Treppe der unzerschnittenen Einzelquadrate unterhalb der Diagonale ergeben sich also

(1)

unzerschnittene Einzelquadrate.

Im Beispiel und (Abb. 7) gibt es Ärger. Die Formel (1) stimmt nicht. Das Ergebnis ist nicht einmal ganzzahlig.

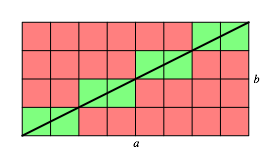
Abb. 7: Die Formel stimmt nicht

Das liegt wohl daran, dass a und b gemeinsame Teiler haben. Um uns diesen Ärger zu ersparen, verlangen wir zusätzlich, dass a und b teilerfremd seien.

Die Abbildung 8 zeigt illustriert, dass der Treppenrhythmus gelegentlich gestört ist. Aber das ist ein Thema für sich.

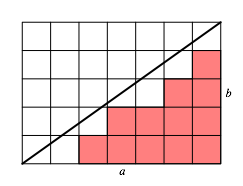
Abb. 8: Stolpertreppe

Zurück zum Beispiel und (Abb. 6). Wir komponieren die Hälften des Rechteckes zu einem Quadrat (Abb. 9). In der Mitte bleibt ein quadratisches Loch der Seitenlänge übrig, welches wir mit unzerschnittenen Einzelquadraten füllen.

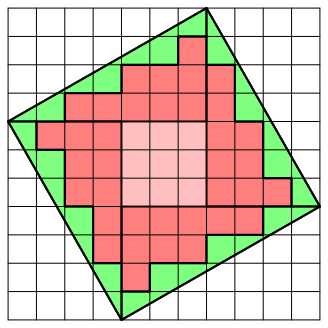
Abb. 9: Das Quadrat

Für die Gesamtanzahl R der unzerschnittenen roten Einzelquadrate erhalten wir daher und wegen (1):

(2)

Die Summe ist die kleine Schwester des Pythagoras.

5 Zerschneidungen

Wir zerschneiden in einem Raster mit b Spalten nebeneinander und a Zeilen untereinander (Abb. 10a). Darin führen wir die benötigten Zerschneidungen durch (Abb. 10b).

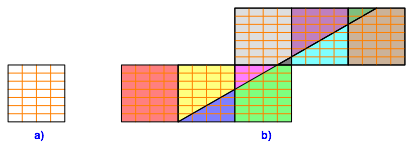
Abb. 10: Zerschneidung

Die Abbildung 11 schließlich zeigt den Zerschneidungsbeweis für unser Beispiel in aller Herrlichkeit und auf 95% reduziert.

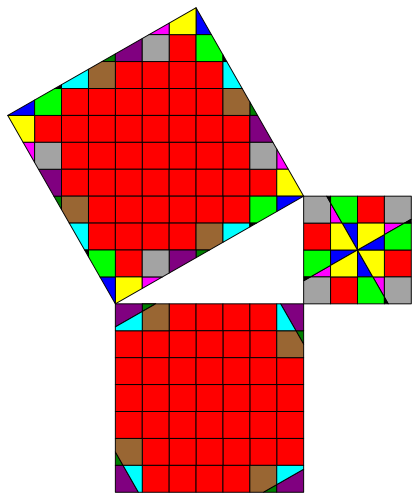
Abb. 11: Pythagoras