Hans Walser, [20150723]
Verallgemeinerung der Kegelschnitte
1 Worum es geht
Die Kegelschnitte werden in zweierlei Hinsicht verallgemeinert:
á Verwendung einer allgemeinen p-Norm
á Mehrere Brennpunkte
2 Norm
Die bliche Abstandsnorm (Pythagoras-Norm)
![]()
verallgemeinern wir zu:
![]()
Fr p = 2 ergibt sich die bliche Pythagoras-Norm.
Die
Abbildung 1 zeigt die Einheitskreise fr ![]() .
.
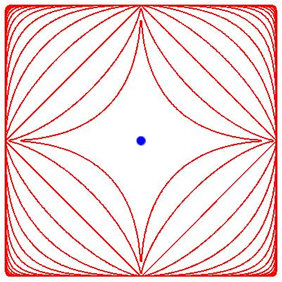
Abb. 1: Einheitskreise
Wir erkennen zuinnerst die Astroide (dass die Spitzen nicht ganz ausgefahren werden, hat mit Auflsungsproblemen zu tun), dann als bernchstes ein spitzstndiges Quadrat und als bernchstes den gewhnlichen Kreis. Die Figuren streben fr wachsende n gegen ein bodenstndiges Quadrat.
Die
Abbildung 2 zeigt das Entsprechende fr Ellipsen mit den Brennpunkten ![]() und
und ![]() sowie der
Abstandssumme (Schnurlnge bei der Grtnerkonstruktion) 4.
sowie der
Abstandssumme (Schnurlnge bei der Grtnerkonstruktion) 4.
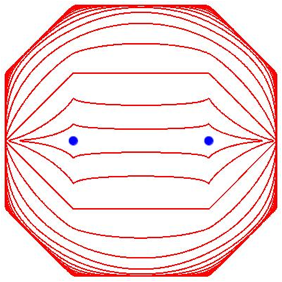
Abb. 2: Ellipsen
Zuinnerst sehen wie die Astrollipse, dann als bernchstes einen Diamanten und wieder als bernchstes die gewhnlichen Ellipse. Fr wachsendes n streben die Figuren gegen ein gleichwinkliges aber nicht gleichseitiges Achteck.
Jetzt ist es spannend, wie es bei Hyperbeln (Abb. 3) und Parabeln (Abb. 4) luft.
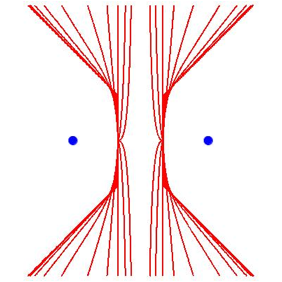
Abb. 3: Hyperbeln
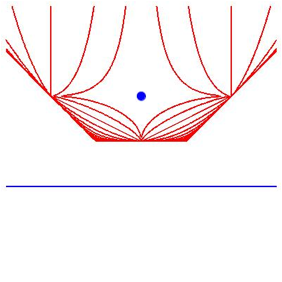
Abb. 4: Parabeln
3 Konfokale Scharen
Bis jetzt haben wir die Metrik variiert. Wir knnen auch konfokale Kurvenscharen bei konstanter Metrik ansehen.
Die Abbildung 5 zeigt konfokale Ellipsen im blichen Sinn.
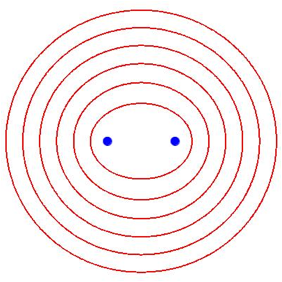
Abb. 5: Konfokale Ellipsen
Die
Abbildung 6 zeigt dieselben Ellipsen in den Metriken ![]() .
.
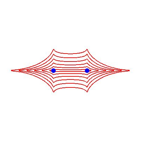
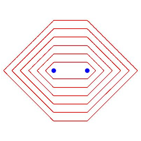
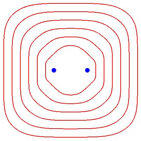
Abb. 6: Verschiedene Metriken
Fr die Metrik mit p = 1 ergeben sich immer geradlinige Polygonzge als Kurven.
4 Mehrere Brennpunkte
Die Abbildung 7 zeigt eine konfokale Ellipsenschar mit drei Brennpunkten. Wir arbeiten mit der Metrik p = 2.
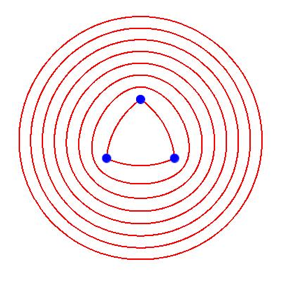
Abb. 7: Drei Brennpunkte
Die Idee dahinter ist einfach: Wir halten die Abstandssumme zu den drei Brennpunkten konstant.
Wenn wir
nun mit anderen Metriken arbeiten, zum Beispiel wieder mit ![]() , erleben wir eine berraschung (Abb. 8).
, erleben wir eine berraschung (Abb. 8).
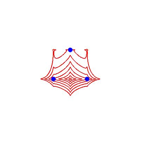
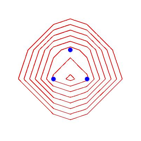
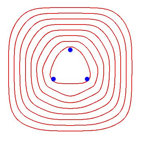
Abb. 8: Andere Metriken
Die
dreiteilige Symmetrie ist weg. Die Scharkurven der Abbildung 7 haben dieselben
Symmetrien wie das gleichseitige Dreieck mit den Brennpunkten in den Ecken. In
der Abbildung 8 haben wir nur noch eine senkrechte Achsialsymmetrie. Der Grund
liegt darin, dass die Metriken mt ![]() am
Koordinatensystem orientiert sind. Nur die Ausnahmemetrik mit p = 2 ist vom Koordinatensystem
unabhngig und damit eine rein geometrisch brauchbare Metrik. Das illustriert
die Bedeutung des Satzes von Pythagoras.
am
Koordinatensystem orientiert sind. Nur die Ausnahmemetrik mit p = 2 ist vom Koordinatensystem
unabhngig und damit eine rein geometrisch brauchbare Metrik. Das illustriert
die Bedeutung des Satzes von Pythagoras.
Die Abbildungen 8 und 9 zeigt ein Beispiel mit vier Brennpunkten, die aber bezglich des Koordinatensystems schief liegen. Fr p = 2 liegt nichts Besonderes vor (Abb. 8). Die Scharkurven haben dieselben Symmetrien wie das Brennpunktequadrat.
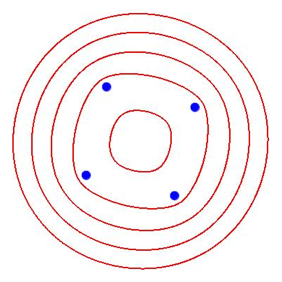
Abb. 9: Vier Brennpunkte
Fr ![]() sieht es
anders aus (Abb. 10).
sieht es
anders aus (Abb. 10).
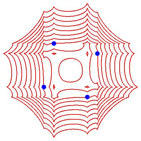
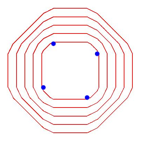
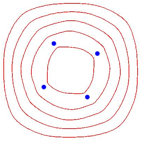
Abb. 10: Andere Metriken
Die Scharkurven haben zwar noch eine vierteilige Drehsymmetrie, aber keine Symmetrieachsen wie das Brennpunktequadrat.
5 Anziehende und absto§ende Brennpunkte
Bis jetzt haben wir alle Brennpunktabstnde additiv berechnet. Wir knnen aber auch einzelne Brennpunktabstnde subtraktiv aufnehmen. Die zugehrigen Brennpunkte werden als absto§ende Brennpunkte bezeichnet und mit einem spitzstndigen Quadrat dargestellt. Die Abbildung 11 zeigt ein Beispiel mit zwei anziehenden und einem absto§enden Brennpunkt fr p = 2.
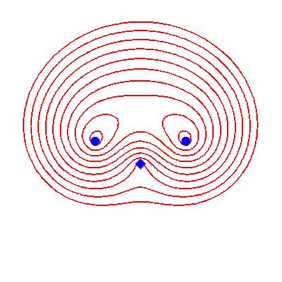
Abb. 11: Unterschiedliche Brennpunkte
Die
Abbildung 12 zeigt dieselben Kurvenscharen fr ![]() .
.
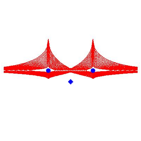
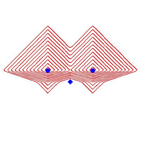
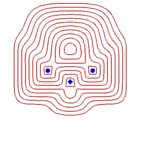
Abb. 12: Verschiedene Metriken
Die Abbildung 13 zeigt drehsymmetrisch verteilte Brennpunkte mit p = 2.
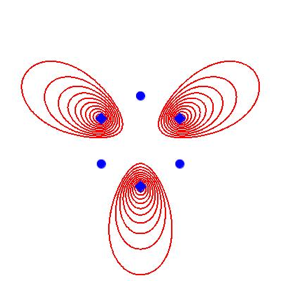
Abb. 13: Drehsymmetrisch verteilte Brennpunkte
Bei
anderen Metriken (![]() ) gibt es wiederum Probleme mit der Symmetrie (Abb.
14).
) gibt es wiederum Probleme mit der Symmetrie (Abb.
14).
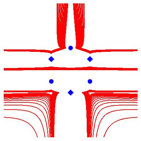
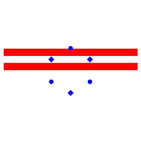
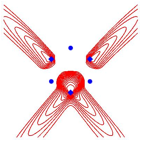
Abb. 14: Keine Drehsymmetrie
In der Abbildung 15 (mit p = 2) sind die Brennpunkte kompatibel zum Koordinatensystem gewhlt.
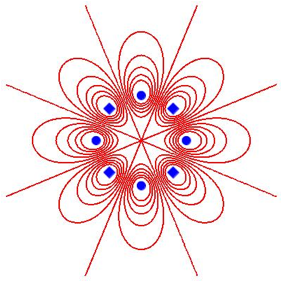
Abb. 15: Symmetrie zum Koordinatensystem
Die Abbildung 16 zeigt das entsprechende fr andere Metriken.
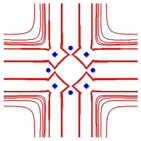

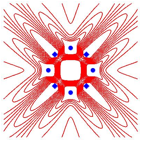
Abb. 16: Andere Metriken