Hans Walser, [20120721]

Allgemeine pythagoreische Dreiecke

1 Worum geht es?

Zu einem vorgegebenen Winkel mit suchen wir passende Dreiecke mit .

Im Sonderfall sind das die üblichen pythagoreischen Dreiecke.

2 Grundformeln

Kosinussatz:

Wir wählen nun und berechnen:

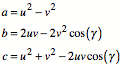
Die so berechneten a, b, c genügen dem Kosinussatz, wie durch Einsetzen verifiziert werden kann. Es ist nämlich:

und ebenso

3 Methode

Wir wählen nun speziell mit . Auf Grund der Voraussetzung ist dann auch . Wir haben also ein rationales Dreieck.

Nun frisieren wir a, b, c, indem wir mit dem kgV aller Nenner multiplizieren. Wir haben jetzt und unsere Aufgabe ist im Prinzip gelöst. Als Schönheitskorrektur dividieren wir noch durch den .

Es zeigt sich, dass wir nun jede Lösung doppelt haben, mit vertauschten Rollen von a und b. Daher standardisieren wir noch auf .

4 Beispiele

4.1 Rechter Winkel

Für den Sonderfall erhalten wir:

u	v	a	b	c
3	1	4	3	5
4	1	15	8	17
5	1	12	5	13
5	2	21	20	29
6	1	35	12	37
7	1	24	7	25
7	2	45	28	53
8	1	63	16	65
8	3	55	48	73
9	1	40	9	41
9	2	77	36	85
10	1	99	20	101
10	3	91	60	109

Das sind die üblichen pythagoreischen Dreiecke, allerdings nicht in der üblichen Reihenfolge.

4.2 Winkel von 60° und 120°

Für , also , erhalten wir:

u	v	a	b	c
2	1	1	1	1
3	1	8	5	7
4	1	15	7	13
5	1	8	3	7
5	2	21	16	19
6	1	35	11	31
7	1	48	13	43
7	2	15	8	13
7	3	40	33	37
8	1	21	5	19
8	3	55	39	49
9	1	80	17	73
9	2	77	32	67
9	4	65	56	61
10	1	99	19	91
10	3	91	51	79

Zuoberst ist das gleichseitige Dreieck.

Die Abbildung zeigt das zweite Beispiel:

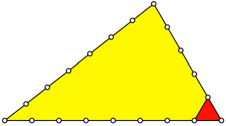
8, 5, 7

Für , also , erhalten wir:

u	v	a	b	c
3	1	8	7	13
4	1	5	3	7
5	1	24	11	31
6	1	35	13	43
7	1	16	5	19
7	2	45	32	67
8	1	63	17	73
9	1	80	19	91
9	2	77	40	103
10	1	33	7	37
10	3	91	69	139

Die Abbildung zeig das zweite Beispiel:

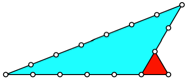
5, 3, 7

4.3

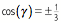
Der Winkel ist ein alter Bekannter. Es ist der Schnittwinkel der Diagonalen im DIN-Rechteck. Es ist auch der Diederwinkel (Schnittwinkel zwischen zwei Seitenflächen) im Tetraeder.

Für erhalten wir:

u	v	a	b	c
3	1	3	2	3
4	1	45	22	43
5	1	18	7	17
5	2	63	52	67
6	1	105	34	99
7	1	18	5	17
7	2	135	76	131
7	3	10	9	11
8	1	189	46	179
8	3	55	42	57
9	1	60	13	57
9	2	231	100	219
9	4	195	184	219
10	1	297	58	283
10	3	91	54	89

Die Abbildung zeigt das oberste Beispiel und den Link mit dem DIN-Format.

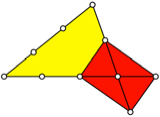
3, 2, 3. Link mit dem DIN-Format

Der Winkel ist der stumpfe Schnittwinkel der Diagonalen im DIN-Rechteck. Es ist auch der Diederwinkel (Schnittwinkel zwischen zwei Seitenflächen) im Oktaeder.

Für erhalten wir:

u	v	a	b	c
3	1	6	5	9
4	1	45	26	59
5	1	9	4	11
6	1	105	38	123
7	1	36	11	41
7	2	135	92	187
8	1	189	50	211
8	3	55	54	89
9	1	30	7	33
9	2	231	116	291
10	1	297	62	323
10	3	91	66	129

Die Abbildung zeigt das oberste Beispiel und den Link mit dem DIN-Format.

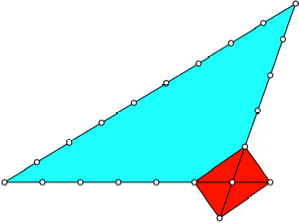
6, 5, 9. Link mit dem DIN-Format

Wer Lust hat, kann sich über das folgende Bild Gedanken machen.

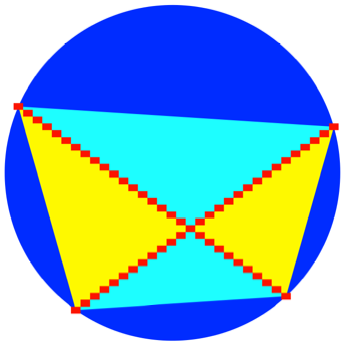
Was steckt hinter diesem Bild?