1 Problemstellung

Zu 2n gegebenen Punkten A_i(x_i,y_i), i = 1 .. 2n suchen wir die Punktmenge:

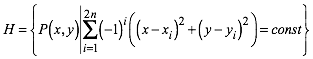(1)

Die alternierende Summe der Quadrate der Abstände soll konstant sein.

Bemerkung: Wenn wir statt der alternierenden Summe die gewöhnliche Summe nehmen, ist H ein Kreis um den Schwerpunkt der gegebenen Punkte (Satz von al-Sijzi).

2 Beispiele

2.1 Zwei Punkte

Bei zwei Punkten ist die Lösung für die Konstante null die Mittelsenkrechte dieser beiden Punkte (Abb. 1).

Abb. 1: Rot = blau

Für andere Konstanten ergeben sich zur Mittelsenkrechten parallele Geraden.

Der Autor ist wohl eine Erklärung schuldig, weshalb er die beiden Quadrate nicht spiegelbildlich gezeichnet hat. Ist doch die Mittelsenkrechte der Archetyp der Geradenspiegel-Symmetrie. Der Grund ist folgender: Ich habe das Quadrat so gezeichnet, dass die Umlaufsorientierung beginnend bei P über A_i immer positiv ist. Dies im Hinblick auf Beispiele mit mehr als zweien Punkten A_i (vergleiche Beispiel 2.2).

2.2 Reguläres Beispiel mit vier Punkten

Gegeben sind vier Punkte gemäß Abbildung 2. Die Punkte sind alternierend gefärbt. Die schwarze Gerade ist die gesuchte Punktmenge gemäß (1) für die Konstante null. Sie wurde mit implicitplot gezeichnet. Der schwarze Punkt ist der Schwerpunkt der vier gegebenen Punkte. Die Gerade verläuft (im allgemeinen) nicht durch den Schwerpunkt. Die Gerade ist also nicht so etwas wie eine Regressionsgerade in der beschreibenden Statistik.

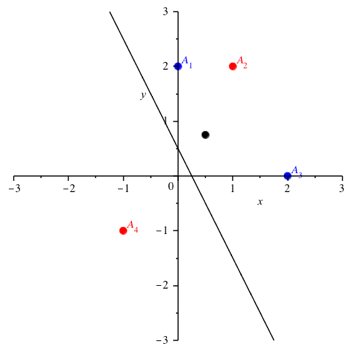
Abb. 2: Konstante null

Die Abbildung 3 illustriert den Sachverhalt mit Quadraten.

Abb. 3: Rot = blau

Die Gleichheit der roten Summe mit der blauen kann mit dem Autostereogramm-Trick überprüft werden. Man schaut durch das Bild hindurch, bis die beiden „Summe“-Wörter zur Deckung kommen. Dann sehen wir, dass auch die Zahlenangaben sich decken.

In der Abbildung 4 haben wir die Geradenschar für die natürlichen Zahlen als Konstanten. Es ist eine Schar von äquidistanten parallelen Geraden.

Abb. 4: Parallelenschar

2.3 Ein singuläres Beispiel

Die vier Punkte A₁, A₂, A₃und A₄ bilden ein Rechteck (Abb. 5.1).

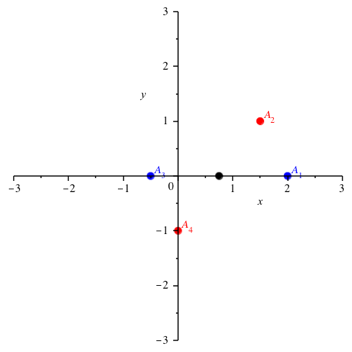
Abb. 5.1: Rechteck

Wenn wir nun mit implicitplot die Menge H für die Konstante null zeichnen, erhalten wir etwas Merkwürdiges (Abb. 5.2).

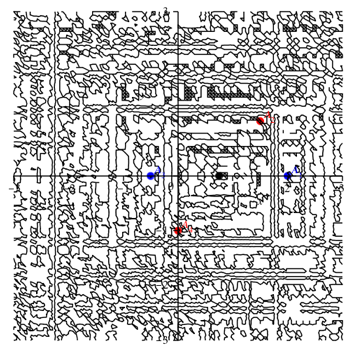
Abb. 5.2: Was ist denn hier los?

Für die Konstante 1 erhalten wir gar nichts, also nur die Abbildung 5.1.

3 Bearbeitung

Es ist:

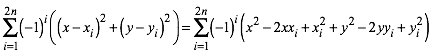(2)

Wegen den alternierenden Vorzeichen fallen alle x² und alle y² weg. Somit ist die Summe ein linearer Ausdruck in x und y. Die Punktmenge H also eine Gerade. Wenigstens im Regelfall.

Bemerkung: Wenn wir statt der alternierenden Summe die gewöhnliche Summe nehmen, ergeben sich 2nx² und 2ny². Daraus folgt, dass die Punktmenge ein Kreis ist.

Wenn in (2) einer der beiden Koeffizienten von x beziehungsweise y verschwindet, ergibt sich eine achsenparallele Gerade. Wenn beide verschwinden, gibt es entweder keine Lösung oder die ganze Ebene als Lösung. Letzteres ist im Beispiel der Abbildung 5.2 der Fall. Es sollte eigentlich die ganze Ebene schwarz sein.

Beim Rechteck der Abbildung 5.1 ist also für jeden Punkt P der Ebene die alternierende Summe der Quadrate der Abstände null.

Weitere solche singuläre Beispiele mit der Konstanten null sind zwei aufeinander fallende Punkte A₁ = A₂ sowie alle regelmäßigen 2n-Ecke. Es gibt aber noch weitere singuläre Beispiele.

In höheren Dimensionen funktioniert die Sache analog. Im Regelfall erhalten wir eine Schar von parallelen Hyperebenen.

Websites

Hans Walser: Al-Sijzi

http://www.walser-h-m.ch/hans/Miniaturen/A/Al-Sijzi5/Al-Sijzi5.htm

Hans Walser: Alternierende Quadratsummen
http://www.walser-h-m.ch/hans/Miniaturen/A/Alternierende_Quadratsummen/Alternierende_Quadratsummen.htm

Hans Walser: Autostereogramm
http://www.walser-h-m.ch/hans/Miniaturen/A/Autostereogramm/Autostereogramm.htm