Hans Walser, [20090117a], [20151203]
Alternierende Quadratsummen
1 Worum geht es?
Es werden Quadratketten konstruiert, deren alternierende Flchensumme null ist.
2 Vieleck mit aufgesetzten Quadraten
2.1 Die Quadratkette
In einem
Vieleck mit Eckenzahl n whlen wir
einen Punkt P und fllen die Lote auf
die Seiten. Dann setzen wir Quadrate auf gem§ Abbildung 1 (Figur fr ![]() ). Die alternierende Quadratflchensumme ist null.
). Die alternierende Quadratflchensumme ist null.
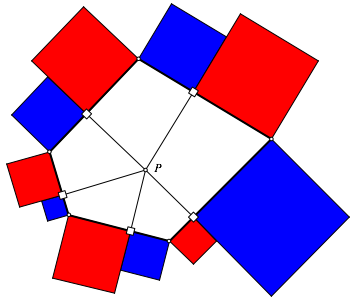
Abb. 1: rot = blau
2.2 Beweis
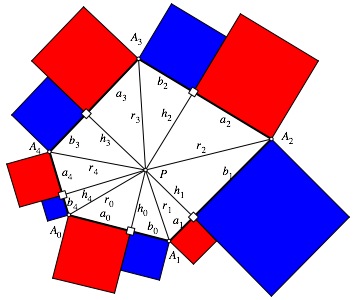
Abb. 2: Beweisfigur
Wir ergnzen gem§ Figur und beschriften und nummerieren zyklisch. Damit gilt:
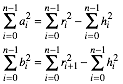 (1)
(1)
Wegen der
zyklischen Nummerierung modulo n ist ![]() . Daraus folgt:
. Daraus folgt:
Das ist die Behauptung.
2.3 Dreieck
Im Dreieck gilt allgemein die Figur der Abbildung 3.
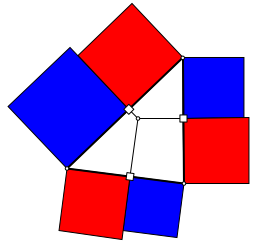
Abb. 3: rot = blau
2.4 Sonderfall im Dreieck
Wir schieben nun den Punkt P in eine Dreiecksecke (Abb. 4). Dann entsteht eine Figur mit einer Dreieckshhe und nur vier Quadraten.
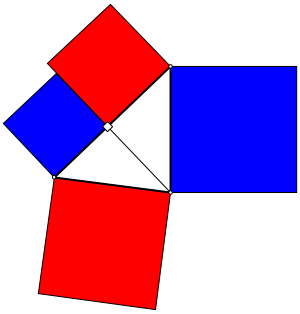
Abb. 4: rot = blau
3 Frage der Umkehrung
3.1 Dreieck
Im Dreieck gilt auch die Umkehrung. Wenn die alternierende Quadratsumme verschwindet, schneiden sich die Orthogonaltrajektorien in einem Punkt.
Wir arbeiten mit den Bezeichnungen der Abbildung 5.
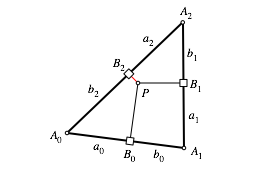
Abb. 5: Bezeichnungen
Zunchst gelten folgende vier Bedingungen:
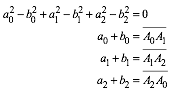 (3)
(3)
Wenn wir nun
zustzlich ![]() und
und ![]() whlen, werden
zum Beispiel
whlen, werden
zum Beispiel ![]() und
und ![]() festgelegt. Zusammen
mit (3) haben wir nun ein Gleichungssystem fr
festgelegt. Zusammen
mit (3) haben wir nun ein Gleichungssystem fr ![]() und
und ![]() ,
, ![]() . Dieses gibt uns
. Dieses gibt uns ![]() und damit rein
rechnerisch die Position von
und damit rein
rechnerisch die Position von ![]() .
.
Andererseits
legen ![]() und
und ![]() den Punkt P fest und vermge Abschnitt 2.1 denselben
Punkt
den Punkt P fest und vermge Abschnitt 2.1 denselben
Punkt ![]() . Das hei§t, dass die Orthogonaltrajektorien durch
. Das hei§t, dass die Orthogonaltrajektorien durch ![]() ,
, ![]() , kopunktal sind.
, kopunktal sind.
3.2 Viereck
Im Viereck gilt die Umkehrung nicht. Die Abbildung 6 zeigt ein Gegenbeispiel.
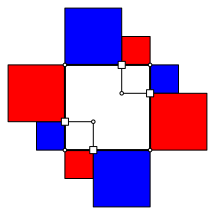
Abb. 6: Gegenbeispiel
Analoge Gegenbeispiele knnen fr Eckenzahlen > 4 konstruiert werden.
4 Verallgemeinerung
4.1 Quadratkette
Wir gehen zurck zum Fall des Vieleckes mit n Ecken und whlen auf jeder Lotgeraden durch P einen beliebigen Punkt. Dann ergnzen wir gem§ Abbildung 7. Wiederum verschwindet die alternierende Quadratsumme.
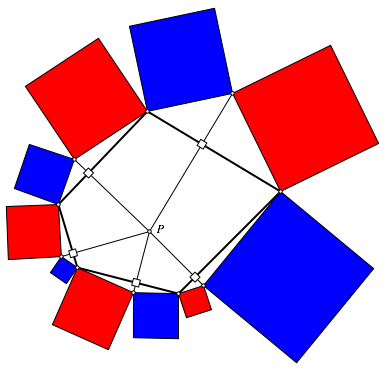
Abb. 7: rot = blau
4.2 Beweis
Wir beschriften und nummerieren zyklisch gem§ Abbildung 8.
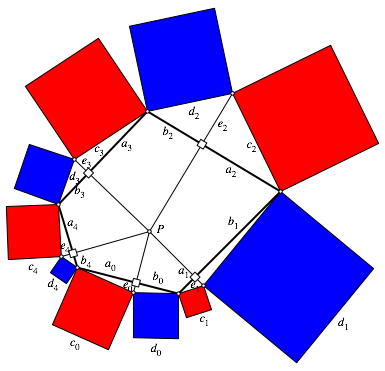
Abb. 8: Beweisfigur
Damit gilt:
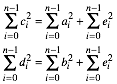 (4)
(4)
Wegen ![]() ist auch
ist auch ![]() . Das ist die Behauptung.
. Das ist die Behauptung.
4.3 Eine Schnittpunkteigenschaft im Dreieck
In einem (ersten) Dreieck (grn in Abb. 9) whlen wir einen Punkt P und fllen die Lote auf die Dreiecksseiten. Auf jedem Lot whlen wir einen beliebigen Punkt und verbinden diese drei Punkte zu einem (zweiten) Dreieck (orange in Abb. 9). Nun fllen wir von den Ecken des ersten (grnen) Dreiecks aus je das Lot auf eine Seite des zweiten (orangen) Dreiecks gem§ Abbildung 9. Diese drei Lote schneiden sich in einem gemeinsamen Punkt Q.
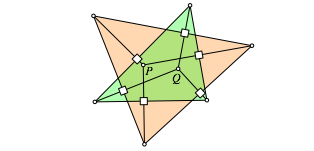
Abb. 9: Schnittpunkt Q
Die entstehende Figur ist begrifflich symmetrisch.
Zu den Ecken knnen wir Quadrate einzeichnen, deren alternierende Summe verschwindet (Abb. 10).
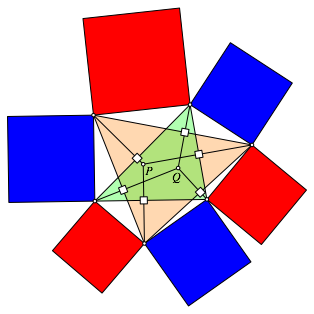
Abb. 10: Alternierende Quadrate
4.4 Sonderfall im Dreieck
Wir whlen den Punkt P als Hhenschnittpunkt und schneiden die Lotgeraden mit dem Umkreis (Abb. 11).
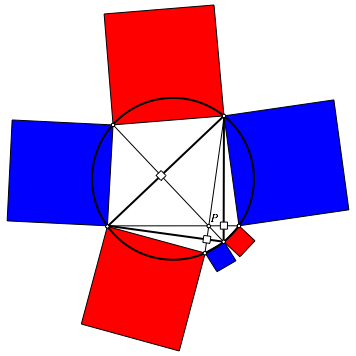
Abb. 11: Sonderfall im Dreieck
Die Quadrate sind dann paarweise kongruent. Beweis?
5 Orthogonales Achsenkreuz
Wir whlen auf den Achsen eines orthogonalen Achsenkreuzes je zwei beliebige Punkte und ergnzen mit Quadraten gem§ Abbildung 12. Wiederum verschwindet die alternierende Quadratsumme. Beweis?
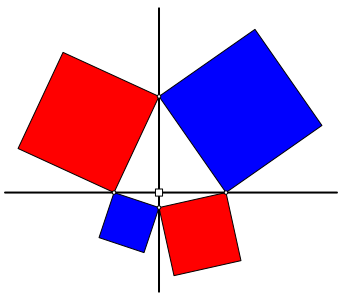
Abb. 12: Achsenkreuz