Hans Walser, [20100424a]

Amboss

1        Worum es geht

Anno salutis 2010 geisterte eine Aufgabe durch den pŠdagogischen BlŠtterwald, wo es um einen BehŠlter gemŠ§ Abbildung ging:

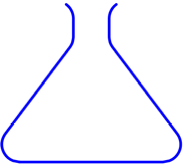
BehŠlter, Umriss

Der BehŠlter wird aus einem tropfenden Wasserhahn gleichmŠ§ig gefŸllt. Gefragt ist ein Kommentar Ÿber die FŸllhšhe in Funktion der Zeit. Insbesondere wird suggeriert, dass die FŸllhšhe linear mit der Zeit wŠchst.

Es handelt sich um eine offene Aufgabe. Das hei§t, jede Antwort ist richtig und daher sind alle SchŸlerinnen und SchŸler gemŠ§ HarmoS-Vorgaben gleichwertig begabt.

2        Lineare Zunahme der FŸllhšhe?

NatŸrlich denkt man an den Chemieunterricht, wo es solche Flaschen gab, welche Erlenmeyer genannt wurden.

Erlenmeyer

Im konischen Teil wŠchst die FŸllhšhe rasant, wie man aus dem FŸllen des konischen Teils einer PET-Flasche wei§, und dann spritzt es oben heraus.

3        Lineare Zunahme der FŸllhšhe

Sollte die FŸllhšhe wirklich linear mit der Zeit wachsen, muss die QuerschnittflŠche konstant sein.

Wenn wir, Erlenmeyer zu Ehren, den Boden kreisfšrmig lassen, arbeiten wir weiter oben am besten mit Ellipsen, deren FlŠche konstant bleibt. Der Kreuzriss (Ansicht gegenŸber dem Umriss oben um 90¡ gedreht) hat dann eine Profilfunktion, welche der Kehrwert der Profilfunktion des Umrisses ist.

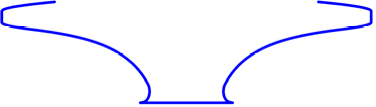
Kreuzriss

Der BehŠlter erhŠlt eine Form, welche an einen Amboss erinnert.

BehŠlter

      

        Umriss von vorn                               Kreuzriss von der Seite

 

 

Untersicht

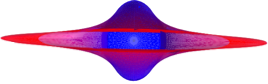
Sicht von oben

4        Symmetrisierung

Wie muss  das Ding aussehen, damit Umriss und Kreuzriss kongruent sind?

Eine mšgliche Lšsung arbeitet mit Exponentialfunktionen:

x:=(u,v)->exp(u)*cos(v):

y:=(u,v)->exp(-u)*sin(v):

z:=(u,v)->u:

 

u=-1..1, v=0..2*PI

Symmetrischer Amboss

    

Umriss von vorne                           Kreuzriss von der Seite

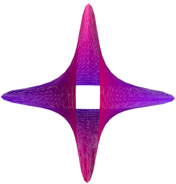
Sicht von oben