Hans Walser, [20190831]

Ameise

Idee und Anregung: Moore 2019

1 Worum geht es?

„Stellen Sie sich eine Ameise vor, die auf einem Gummiseil läuft, dessen Länge beliebig gestreckt werden kann. Nehmen wir an, die Ameise kriecht mit einer Geschwindigkeit von einem Zentimeter pro Sekunde, um das Ende eines einen Meter langen Seils zu erreichen. Während sie läuft, wird das Seil mit einer Geschwindigkeit von einem Meter pro Sekunde gespannt. Das bedeutet: Nach einer Sekunde ist die Ameise einen Zentimeter gelaufen, das Seil ist jetzt aber zwei Meter lang.“ (Moore 2019).

Die Frage ist, ob die Ameise das Ende des Gummiseils erreichen kann.

2 Überschlagsüberlegung

Für unsere Überschlagsrechnung nehmen wir die jeweilige Länge des Gummiseils als Einheit. Da diese Einheit gegenüber der Standardeinheit linear zunimmt, nimmt die Geschwindigkeit der Ameise umgekehrt proportional zur Zeit ab. Aufintegriert gibt das den Logarithmus. Dieser divergiert. Die Ameise erreicht also das Ende des Gummiseils.

Auf die Standardeinheit umgerechnet kommt noch ein Linearfaktor dazu.

3 Formales Vorgehen

Länge des Gummiseils:

(1)

Subjektiv zurückgelegter Weg der Ameise (lineare Funktion in t):

(2)

Man beachte, dass dt kein Differential ist, sondern das Produkt von d mit t. Das Differential schriebe man lege artis dt.

Im Eingangsbeispiel ist die Spanngeschwindigkeit b des Gummiseils hundertmal so groß wie das Tempo d der Ameise.

Mit bezeichnen wir den Abstand der Ameise vom Anfangspunkt des Gummiseils. Wir nehmen an, dass der Anfangspunkt festbleibt und der Endpunkt gemäß (1) gespannt wird. Somit ist:

(3)

4 Differentielles Vorgehen

Was passiert in der Zeiteinheit dt? Es ist einerseits:

(4)

Andererseits ist wegen (2):

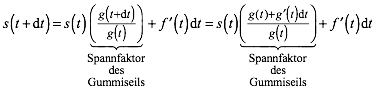(5)

Beim Spannen des Gummiseils wird die Ameise jeweils mitgenommen. Sie bewegt sich daher viel schneller als sie subjektiv meint.

Aus (1), (4) und (5) ergibt sich:

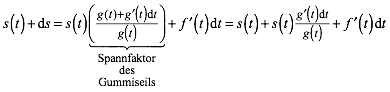(6)

Daraus erhalten wir die Differentialgleichung:

(7)

Zusammen mit der Anfangsbedingung (3) hat (7) die Lösung:

(8)

Wir haben das Produkt einer linearen Funktion mit einer Logarithmusfunktion, wie schon in der Überschlagsüberlegung. Dieses Produkt ist „stärker“ als die lineare Funktion (1). Die Ameise erreicht also das Ende des Gummiseils.

Die Ameise erreicht das Ende des Gummiseils nach

(9)

Zeiteinheiten.

5 Beispiele

5.1 Erstes Beispiel

Wir setzen a = 1, b = 1, c = 0, . Die Abbildung 1 zeigt blau den Verlauf von (1), also das Längenwachstum des Gummiseils in Abhängigkeit der Zeit und rot den Verlauf von (8). Die Ameise erreicht das Ende des Gummiseils nach Zeiteinheiten.

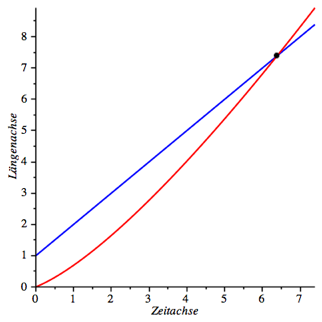
Abb. 1: Erstes Beispiel

5.2 Zweites Beispiel

Wir setzen a = 1, b = 1, c = 0, d = 0.01. Diese Daten entsprechen dem Beispiel in Moore 2019. Die Abbildung 2 zeigt blau den Verlauf von (1), also das Längenwachstum des Gummiseils in Abhängigkeit der Zeit und rot den Verlauf von (8). Die Ameise erreicht das Ende des Gummiseils nach Sekunden. Dies sind etwa Jahre.

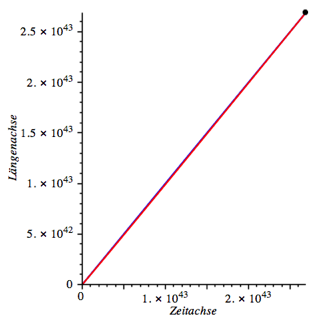
Abb. 2: Astronomisches Beispiel

5.3 Drittes Beispiel

Wir setzen a = 1, b = 1, c = 0, d = 1. In diesem Beispiel wird:

(10)

Die Abbildung 3 zeigt blau den Verlauf von (1), also das Längenwachstum des Gummiseils in Abhängigkeit der Zeit und rot den Verlauf von (8) respektive (9). Die Ameise erreicht das Ende des Gummiseils nach Zeiteinheiten.

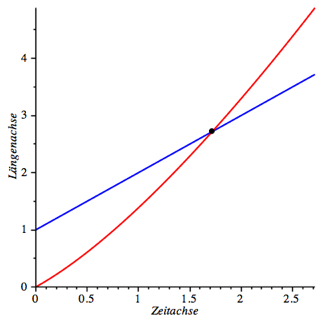
Abb. 3: Interessantes Beispiel

6 Varianten mit exponentiellem Wachstum

6.1 Das Gummiseil wird exponentiell gespannt

6.1.1 Gedankenexperiment

Zuerst ein Gedankenexperiment. Wir lassen in jeder Zeiteinheit zuerst die Ameise krabbeln und spannen anschließend das Gummiseil. Die Ameise krabbelt mit einem Meter pro Zeiteinheit. Das Gummiseil wird nach jeder Zeiteinheit längenmäßig verdoppelt.

Je nach der Startlänge des Gummiseils sieht es nun unterschiedlich aus.

6.1.1.1 Startlänge 1.5m

Bei einer Startlänge des Gummiseils von 1.5m schafft die Ameise in der ersten Zeiteinheit einen Meter und hat noch einen halben Meter vor sich. Nun werden die Längen verdoppelt, die Ameise hat jetzt einen Meter vor sich, den sie in der zweiten Zeiteinheit schafft. Geschafft.

6.1.1.2 Startlänge 2m

Bei einer Startlänge des Gummiseils von 2m schafft die Ameise in der ersten Zeiteinheit einen Meter und hat noch einen Meter vor sich. Nun werden die Längen verdoppelt, die Ameise hat jetzt zwei Meter vor sich und ist wieder in derselben Situation wie am Anfang. Und ewig rauschen die Wälder.

6.1.1.3 Startlänge 2.5m

Bei einer Startlänge des Gummiseils von 2.5m schafft die Ameise in der ersten Zeiteinheit einen Meter und hat noch einen 1.5m vor sich. Nun werden die Längen verdoppelt, die Ameise hat jetzt drei Meter vor sich, schlimmer als am Anfang. Die Ameise gerät immer mehr ins Hintertreffen.

6.1.2 Formalisierung

Wir ändern (1) ab in:

(11)

Am Fortkommen (2) der Ameise ändern wir nichts. Es bleibt hier bei einer linearen Funktion.

Wir zeigen wie oben drei exemplarisch verschiedene Fälle.

6.1.2.1 Erstes Beispiel

Es sei a = 0, b = 1. Die Spannfunktion für das Gummiseil ist die Standard-Exponentialfunktion. Weiter sei c = 0 und d = 2. Für die Differentialgleichung (7) erhalten wir die Lösung:

(12)

Das ist ebenfalls eine Exponentialfunktion. Dies, obwohl sich die Ameise subjektiv nur linear bewegt. Die Abbildung 4 zeigt das Weg-Zeit-Diagramm.

Die Ameise erreicht das Ende des Gummiseils nach Zeiteinheiten.

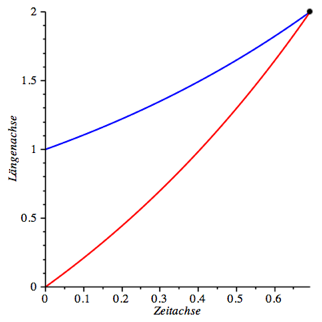
Abb. 4: Die Ameise schafft es

6.1.2.2 Zweites Beispiel

Es sei immer noch a = 0, b = 1. Die Spannfunktion für das Gummiseil ist die Standard-Exponentialfunktion. Weiter sei c = 0. Den Koeffizienten d ändern wir ab in d = 1. Für die Differentialgleichung (7) erhalten wir nun die Lösung:

(13)

Das ist ebenfalls die Exponentialfunktion, aber um eine Längeneinheit nach unten verschoben (Abb. 5). Die Ameise hat immer eine Längeneinheit vor der Nase (haben Ameisen eine Nase?).

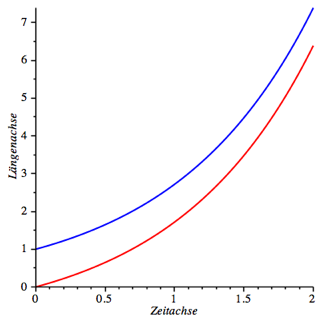
Abb. 5: Die frustrierte Ameise

6.1.2.3 Drittes Beispiel

Es sei nach wie vor a = 0, b = 1. Die Spannfunktion für das Gummiseil ist die Standard-Exponentialfunktion. Weiter sei c = 0. Den Koeffizienten d ändern wir ab in d = 0.5. Für die Differentialgleichung (7) erhalten wir nun die Lösung:

(14)

Die Abbildung 6 zeigt die Situation. Die Ameise gerät immer mehr ins Hintertreffen.

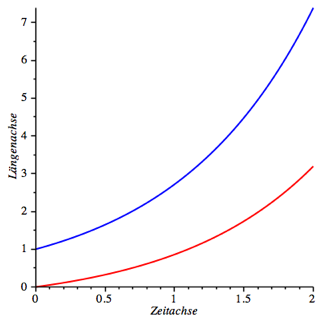
Abb. 6: Der Abstand zum Ziel wächst exponentiell

6.2 Beide Komponenten wachsen exponentiell

Wir ändern nun auch (2) ab, nämlich in:

(15)

Beispiel: Es sei a = 0, b = 1. Die Spannfunktion für das Gummiseil ist die Standard-Exponentialfunktion. Weiter sei c = –1 und d = 1. Für die Differentialgleichung (7) erhalten wir die Lösung:

(16)

Die Ameise schafft es in einer Zeiteinheit (Abb. 7).

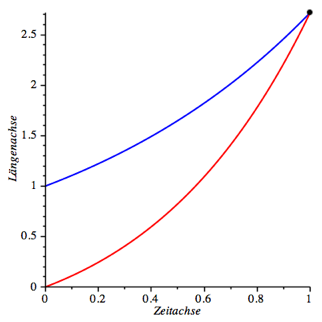
Abb. 7: Die Ameise schafft es locker

Literatur

Moore, Ben (2019): Rasende Ameisen und reisende Photonen. Das Magazin. No 35 – 31. August 2019. S. 7.