1 Worum es geht

Anschlagkonstruktion für das regelmäßige Neuneck.

Nach einem Satz von Gauß ist das regelmäßige Neuneck nicht mit Zirkel und Lineal konstruierbar. Damit sind auch das regelmäßige 18-Eck sowie die Winkel 5°, 10°, 20° , 40°, 80° etc. nicht mit Zirkel und Lineal konstruierbar. Es geht aber mit einer Anschlagkonstruktion.

2 Das Gerät

Die Abbildung 1 zeigt das Gerät in voller Aktion.

Das gelbe Zahnrad hat die Seitenlänge des gelben gleichseitigen Dreiecks als Teilkreisdurchmesser. Sein Zentrum ist die rechte untere Ecke des Dreiecks. Es ist fix mit dem Dreieck verbunden.

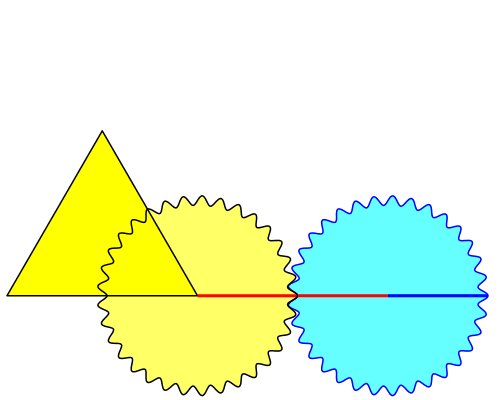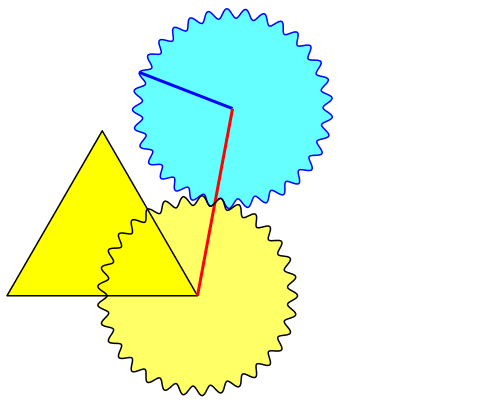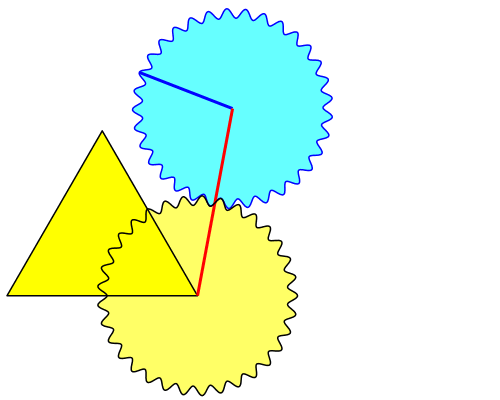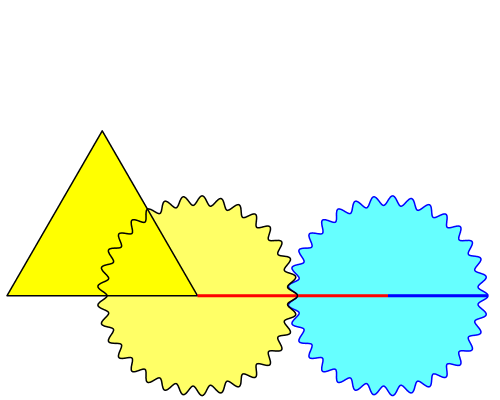
Abb. 1: Das Gerät

Das hellblaue Zahnrad ist gleich groß wie das gelbe. Es wird auf dem gelben abgedreht. Auf dem hellblauen Zahnrad ist ein Radius markiert, welcher in der Startposition horizontal liegt.

Das hellblaue Zahnrad wird gedreht bis zum Anschlag der Radiusmarkierung an der Spitze des Dreiecks. Daher die Bezeichnung „Anschlagkonstruktion“.

Die rote Verbindungsstrecke der beiden Zahnradmitten ist gleich der Seitenlänge des Dreiecks.

3 Geometrische Analyse

In der Abbildung 2 sind zusätzlich zwei Winkel eingezeichnet. Diese Winkel geben die Richtungsänderungen an, zunächst von der Dreiecksgrundseite zur roten Verbindungsstrecke und dann von dieser Verbindungsstrecke zum markierten Radius auf dem hellblauen Zahnrad. Die beiden Richtungsänderungen sind aus Symmetriegründen gleich groß.

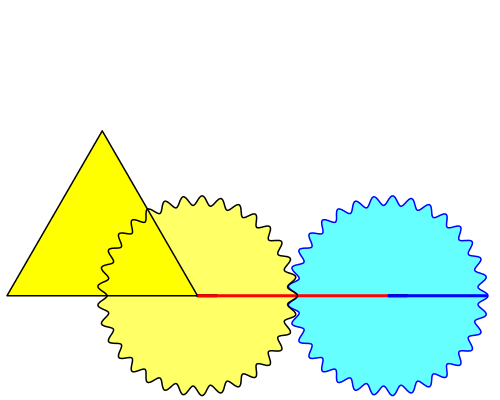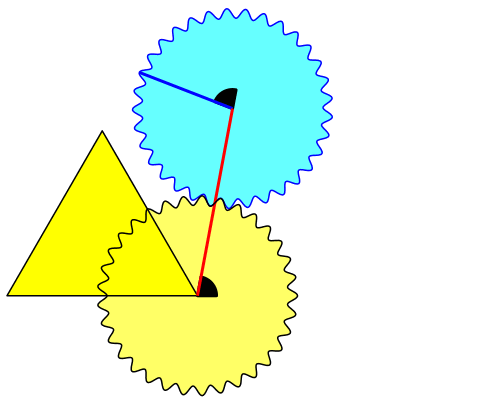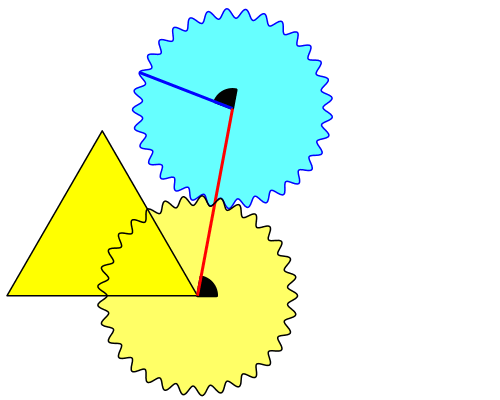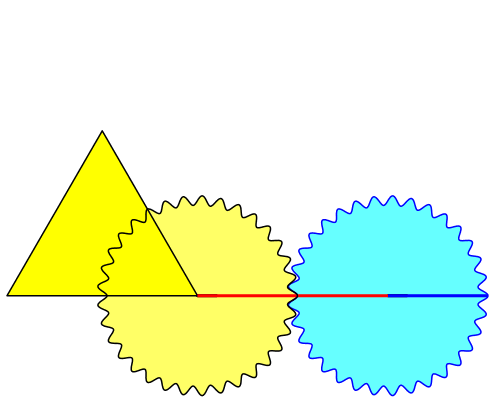
Abb. 2: Richtungsänderungen

Die Abbildung 3 zeigt die Situation am Anschlag. Die Richtungsänderung bis zum Anschlag bezeichnen wir mit λ.

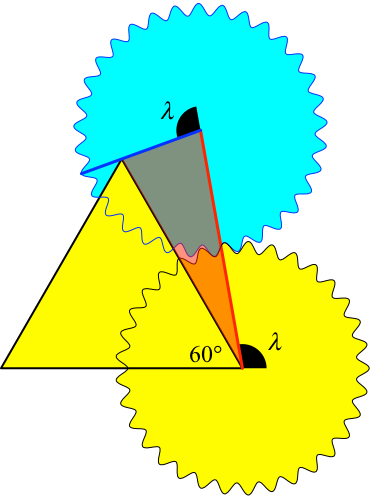
Abb. 3: Am Anschlag

Wir erhalten ein gleichschenkliges Dreieck. Die Richtungsänderung λ ist der Außenwinkel der beiden Basiswinkel. An der Spitze des gleichschenkligen Dreiecks ist der Außenwinkel insgesamt λ + 60°.

In einem Vieleck ist die Außenwinkelsumme 360°. Wir haben für λ also die Bedingung:

λ + λ + (λ + 60°) = 360°

Daraus ergibt sich λ = 100°. Das gleichschenklige Dreieck hat die Basiswinkel 80° und den Spitzenwinkel 20°. Damit haben wir die für das regelmäßige Neuneck (Abb. 4) und das regelmäßige 18-Eck (Abb. 5) relevanten Winkel zur Verfügung.

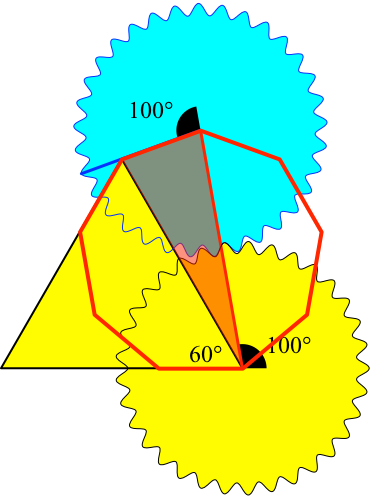
Abb. 4: Regelmäßiges Neuneck

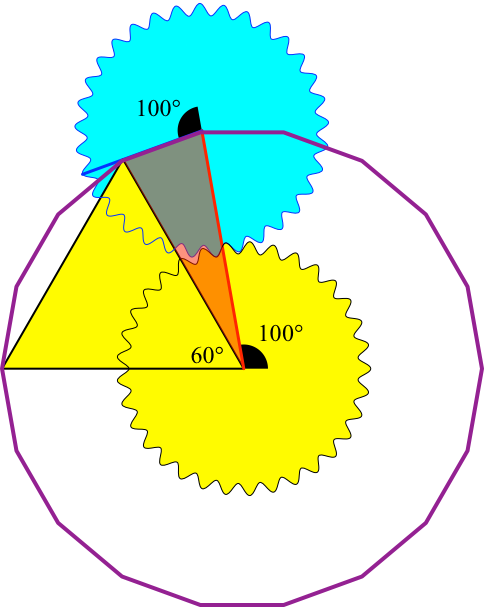
Abb. 5: Regelmäßiges 18-Eck

Weblinks

Hans Walser: 18-Eck

http://www.walser-h-m.ch/hans/Miniaturen/1/18-Eck_2/18-Eck_2.html

Hans Walser: 18-Eck

http://www.walser-h-m.ch/hans/Miniaturen/1/18-Eck/18-Eck.htm