Hans Walser, [20050813a], [20150112]
Antiprismen
Anregung: I. V., L.
1 Worum geht es?
Wenn wir bei einem Prisma mit quadratischer Grundflche die Deckflche um 45¡ verdrehen, entsteht ein Antiprisma mit einer Mantelflche, welche aus gleichschenkligen Dreiecken zusammengesetzt ist. Im Sonderfall von rechtwinklig gleichschenkligen Dreiecken auf der Mantelflche erhalten wir das Antiprisma der folgenden Figur.
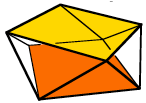
Antiprisma mit quadratischem Boden und quadratischer Deckflche
Wir untersuchen Krper, welche durch Aufeinanderstapeln von mehreren solchen Antiprismen entstehen und gehen insbesondere der Frage nach, wie diese Krper durch Flechtmodelle dargestellt werden knnen.
2 Flechtmodell des Antiprismas
Das Antiprisma kann berraschenderweise durch ein Flechtmodell dargestellt werden, welches einen einzigen Streifen bentigt. Der Streifen setzt sich aus netto 16 Quadraten zusammen; zur Stabilisierung versenden wir zwei zustzliche Quadrate, welche mit den ersten beiden zu berlappen sind. Die blauen Linien sind Faltlinien, alles Berg-Faltlinien.
![]()
Der Streifen
Deckflche und Boden des Flechtmodells bestehen ebenfalls aus rechtwinklig gleichschenkligen Dreiecken.

Antiprisma
Die Flechtstruktur entspricht topologisch einer vierfachen Schlinge. Die folgende Figur zeigt zwei verschiedene Darstellungen der Flechtstruktur


Flechtstruktur
3 Zwei Antiprismen
Wir stapeln nun zwei Antiprismen ber einander. Das Flechtmodell bentigt nun vier Streifen mit je nette 6 Quadraten. In den Streifen sind auch Tal-Faltlinien (rot) ntig. Die Abbildung zeigt einen der vier bentigten Streifen.
![]()
Streifen
Das Flechtmodell kann nun vierfarbig gestaltet werden.

Zwei Antiprismen
Das Modell sieht aus wie ein verdrckter Wrfel. Tatschlich hat es dieselbe Flechtstruktur wie der Schrg-Streifen-Wrfel. Sie besteht aus vier verschlungenen Ringen.

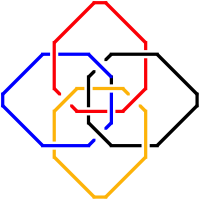
Flechtstruktur
4 Drei Antiprismen
Bei drei aufeinander geschichteten Antiprismen kommt man theoretisch mit einem Streifen der Nettolnge 32 aus. Fr das Flechten bentigte man allerdings mehr als zwei Hnde, so dass ich diesen Streifen in vier Teilstreifen zerlegt habe. Da es aber im Prinzip ein durchgehender Streifen ist, muss fr alle Teilstreifen dieselbe Farbe gewhlt werden.
![]()
Viertel eines Streifens
Das Modell sieht entsprechend monochrom aus.

Drei Antiprismen aufeinander
Die Flechtstruktur besteht aus einem einzigen, verschlungenen String.


Flechtstruktur
5 Vier Antiprismen
Wir bentigen zwei Streifen der Nettolnge 20. In der Flechtpraxis ist es allerdings einfacher, mit vier Halbstreifen der Nettolnge 10 zu arbeiten.
![]()
Halber Streifen
Das Modell kann zweifarbig gestaltet werden; auf der Mantelflche entsteht eine schraubenlinienartige Struktur.

Vier Antiprismen aufeinander
Die Flechtstruktur ist entsprechend zweifarbig.

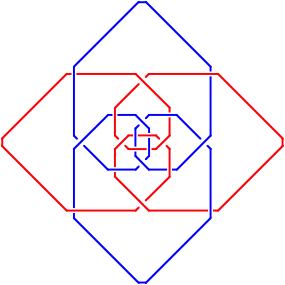
Flechtstruktur
6 Sechs Antiprismen
Hier bentigen wir wieder vier Streifen zu netto je 14 Quadraten.
![]()
Streifen
Das Modell wir vierfarbig.

Sechs Antiprismen
Die Flechtstruktur besteht aus vier mehrfach verschlungenen Kreisen.
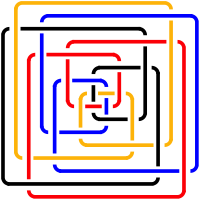
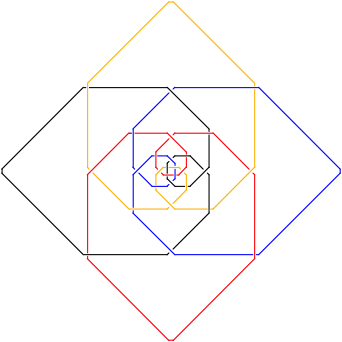
Flechtstruktur
7 Acht Antiprismen
Bei acht Antiprismen, wir ahnen es, gengen zwei Streifen. Sie haben die Nettolnge 36. Wir arbeiten allerdings auch hier mit zweimal zwei Halbstreifen der Nettolnge 18.
![]()
Halbstreifen
Das zweifarbene Flechtmodell weist wieder eine schraubenlinienartige Struktur auf.

Acht Antiprismen
In der Flechtstruktur zeigt sich ein farblicher Doppelrhythmus von innen nach au§en.
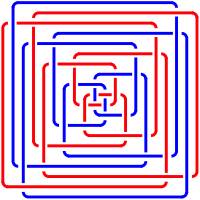
Flechtstruktur
8 bersicht
|
# Antiprismen |
# Streifen |
# Quadrate (netto) |
|
|
total |
pro Streifen |
||
|
1 |
1 |
16 |
16 |
|
2 |
4 |
24 |
6 |
|
3 |
1 |
32 |
32 |
|
4 |
2 |
40 |
20 |
|
5 |
1 |
48 |
48 |
|
6 |
4 |
56 |
14 |
|
7 |
1 |
64 |
64 |
|
8 |
2 |
72 |
36 |