Hans Walser, [20140819]

Anzahl Dreiecke im Dreiecksgitter

Anregung und Idee: T. H., A.

1     Worum es geht

In einem regulŠren Dreiecksgitter mit n Gitterpunkten an einer Seite und Spitze nach oben zeichnen wir gleichseitige Dreiecke ein. Die Dreieckseckpunkte sollen Gitterpunkte sein.

Die Abbildung 1 zeigt ein Beispiel mit n = 9.

 

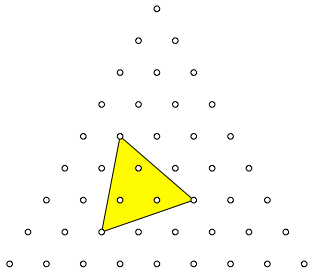
Abb. 1: Dreiecksgitter und Dreieck

 

Gesucht ist die Anzahl  der mšglichen gleichseitigen Dreiecke.

2     Gitterparallele Dreiecke mit Spitze nach oben

Jedes Dreieck kann in ein gitterparalleles Dreieck mit Spitze nach oben einbeschrieben werden (Abb. 2). Das gitterparallele Dreieck ist magenta gezeichnet.

 

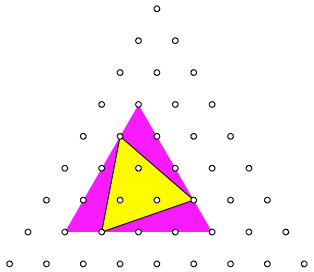
Abb. 2: Gitterparalleles Dreieck mit Spitze nach oben

 

Es gibt  gitterparallele Dreiecke mit Spitze nach oben und KantenlŠnge k. Dabei ist .

3     Einbeschriebene Dreiecke

Umgekehrt kšnnen in ein gitterparalleles Dreieck mit Spitze nach oben und KantenlŠnge k genau k gleichseitige Dreiecke einbeschrieben werden, wobei das gitterparallele Dreieck mitgezŠhlt wird (Abb. 3 fźr k = 4).

 

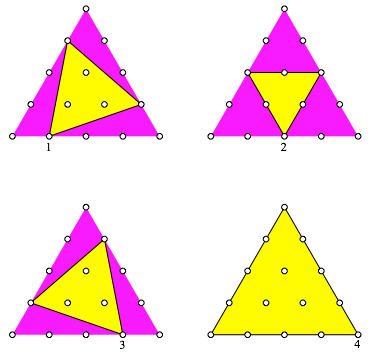
Abb. 3: Einbeschriebene Dreiecke

 

4     Die Anzahl der Dreiecke

Damit erhalten wir fźr die gesuchte Anzahl :

 

 

 

Einsetzen der einschlŠgigen Formeln fźr die drei Summen rechts ergibt:

 

 

5     HaifischzŠhne

Wie viele HaifischzŠhne (gitterparallele Dreiecke mit Spitze nach unten, Abb. 4) gibt es?

 

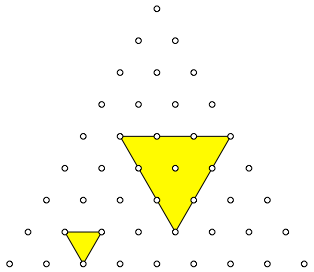
Abb. 4: HaifischzŠhne

 

5.1    Erster Lšsungsweg

Das umbeschriebene gitterparallele Dreieck (mit Spitze nach oben) eines Haifischzahns hat gerade KantenlŠnge. Zu jedem gitterparallelen Dreieck mit Spitze nach oben und gerader KantenlŠnge ist das Seitenmittendreieck ein Haifischzahn. Aus der Formel

 

 

folgt daher:

 

 

 

 

 

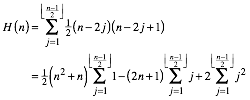
Fallunterscheidung bezźglich der ParitŠt von n.

n gerade: In diesem Fall ist . Wir erhalten:

 

 

 

Mit der źblichen Bearbeitung der einzelnen Summen ergibt sich schlie§lich:

 

 

n ungerade: In diesem Fall ist . Analoge Bearbeitung liefert:

 

 

5.2    Zweiter Lšsungsweg

Experimentieren mit verschiedenen n und verschiedenen k (SeitenlŠngen des Haifischzahns) fźhrt auf folgende Tabelle:

 

n \ k

1

2

3

4

H(n)

2

0

 

 

 

0

3

1

 

 

 

1

4

3

 

 

 

3

5

6

1

 

 

7

6

10

3

 

 

13

7

15

6

1

 

22

8

21

10

3

 

34

9

28

15

6

1

50

Tab. 1: Daten

 

Wir erkennen in den Spalten die Binomialkoeffizienten  mit einem ăhinkendenŇ Hšhenversatz 2.

Es ist:

 

 

 

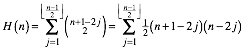
Das ist aber dieselbe Formel wie beim ersten Lšsungsweg.