Hans Walser, [20130203]

Approximation des Goldenen Schnittes

Anregung: T. W., L.

Wir beginnen mit dem regulären Dreiecksraster der Maschenweite (Seitenlänge der Dreiecke) 1 (Abb. 1).

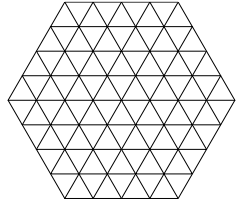
Abb. 1: Dreiecksraster

Nun drehen wir dieses Raster um einen Rasterpunkt um 90° und überlagern mit dem Ausgangsraster (Abb. 2).

Abb. 2: Gedrehtes Raster

Es wird ein Quadratraster sichtbar.

Frage 1: Stehen die blau und rot gezeichnete Strecke der Abbildung 3 im Verhältnis des Goldenen Schnittes?

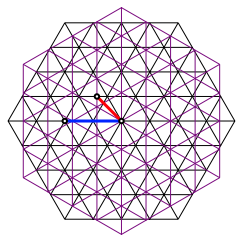
Abb. 3: Goldener Schnitt?

Bearbeitung:

Für die blaue Strecke haben wir die Seitenlänge 2.

Das Quadratraster hat die Maschenweite . Somit haben wir für die rote Strecke die Seitenlänge .

Für das Längenverhältnis ergibt sich:

Das ist etwas mehr als der Goldene Schnitt:

Wir haben lediglich eine Approximation des Goldenen Schnittes.

Frage 2: Kommen in der unendlich ausgedehnt gedachten Figur der Abbildung 2 weitere Rasterpunkt zur Deckung?

Antwort: Nein. Das liegt an der Irrationalität von .