Hans Walser, [20111229a]

Approximation der Zykloide

Idee: R. W., F.

1 Abrollen eines regelmäßigen n-Ecks

Wir rollen ein regelmäßiges n-Eck auf einer Geraden ab und verfolgen den Weg eines partikulären Eckpunktes. Beim Dreieck setzt sich dieser Weg aus zwei Kreisbogen zusammen, welche die Seitenlänge des Dreieckes als Radius haben (Abb. 1). Der Abrollprozess (besser wohl „Abkippprozess“) von links nach rechts wird durch die Farbveränderung von rot zu blau indiziert.

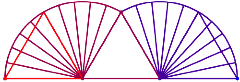
Abb. 1: Abrollen des Dreiecks

Beim Quadrat haben wir drei Kreisbogen, der Radius des mittleren Bogens ist gleich der Quadratdiagonalen.

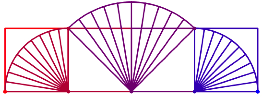
Abb. 2: Abrollen des Quadrates

Beim Siegeneck (Abb. 3) haben wir sechs Bögen, deren Radien der Reihe nach die Längen der von einem Eckpunkt ausgehenden Seiten und Diagonalen sind („Diagonalenfächer“). Bei einem n-Eck haben wir entsprechend Bögen.

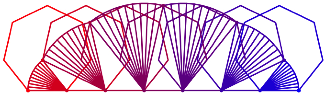
Abb. 3: Abrollen des Siebenecks

Für wachsendes n nähert sich die Bogenfigur der Zykloide an. Die Abbildung 4 zeigt die Situation für .

Abb. 4: Approximation der Zykloiden

2 Bezeichnungen und Berechnungen

Im regelmäßigen n-Eck mit Umkreisradius 1 bezeichnen wir mit den Abstand zweier Punkte und . Damit ist , weiter die Seitenlänge des regelmäßigen n-Ecks, und die Länge einer Diagonalen, welche Punkte überspringt. Den Mittelpunkt des Umkreises bezeichnen wir mit M, den Radius mit r. Die Längen sind also die sukzessiven Radien unserer Kreisbögen. Die zugehöreigen Kreissektoren haben alle den Zentriwinkel .

Da jede Seite von M aus unter einem Winkel von erscheint, ist . Analog ist .

Für die Länge des Bogens mit dem Radius erhalten wir also:

Der letzte Bogen ist nur noch ein Punkt, also . Wir dürfen also im Folgenden die Summationen von 1 bis n laufen lassen, obwohl wir nur Kreisbogen haben.

Für die Gesamtlänge der Kurve erhalten wir:

Wir bearbeiten zunächst die Summe . Dazu setzen wir die Ortsvektoren der entsprechenden Kreisteilungspunkte auf dem Einheitskreis zu einem Polygonzug zusammen. Die Abbildung 5 zeigt die Situation für .

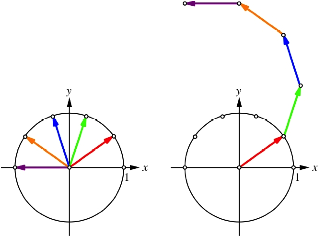
Abb. 5: Polygonzug aus Einheitsvektoren

Wir erhalten ein halbes regelmäßiges der Seitenlänge 1. Die gesuchte Sinus-Summe ist die vertikale „Höhe“ dieses . Dies ist der Inkreisdurchmesser, welcher die Länge hat.

Somit ist:

3 Grenzwert

Für erhalten wir die Zykloide. Wie lang ist diese? Wir suchen den Grenzwert:

3.1 Vermutung

Die Tabelle 1 gibt einige Werte an.

2	6.283185307
3	7.255197457
4	7.584475592
5	7.735062392
10	7.93409415
20	7.983543891
30	7.992687845
40	7.995887242
50	7.997367932
100	7.999342016

Tabelle 1: Werte von

Wir vermuten:

Fällt das tatsächlich raus?

3.2 Beweis

Wir berechnen mit Hilfe der Substitution und unter Anwendung der Regel von Bernoulli-de l’Hôpital. Es ist:

3.3 Differenzielle Herleitung

Wir greifen zurück zur Formel

und führen die Bezeichnung ein. Damit wird:

Für den Grenzübergang können wir schreiben:

Damit wird:

4 Parametrisierung der Zykloide

Die Abbildung 6 ist ein Teil der Abbildung 4. Zusätzlich sind zwei Radien des regelmäßigen 20-Ecks eingezeichnet.

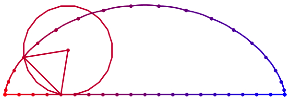
Abb. 6: Figur zum Anschauen

Der Grenzübergang führt entsprechend zur Figur der Abbildung 7 mit der Zykloide.

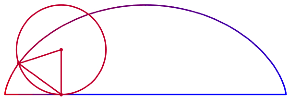
Abb. 7: Zykloide

Wir entnehmen daraus für die Zykloide die Parameterdarstellung:

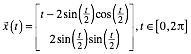
Diese Parameterdarstellung lässt sich umformen zur üblichen Parameterdarstellung:

Sie hat aber rechentechnische Vorteile. Aus

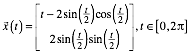
erhalten wir:

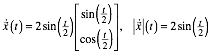
Damit ergibt sich für die Bogenlänge der Zykloide:

Mit der üblichen Parametrisierung wird die Berechnung des Integrals etwas aufwändiger.

5 Eine eigenartige Kurve

Die Abbildung 8 zeigt dasselbe wie die Abbildung 3, aber ohne die Siebenecke. Es sind nur die Sektoren gezeichnet.

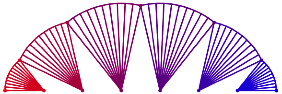
Abb. 8: Nur Sektoren

Nun denken wir uns Figur als ein bewegliches Modell aus Sektoren, welche an den Bogen-Enden gelenkig verbunden sind. In der Situation der Abbildung 8 haben wir zwischen aufeinander folgenden Sektoren jeweils einen Öffnungswinkel von (allgemein ). Nun klappen wir das Modell zusammen, so dass die Zwischenwinkel verschwinden (Abb. 9).

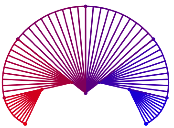
Abb. 9: Zusammengeklappte Sektoren

Die Abbildung 10 bis 12 zeigen die Figuren für , und .

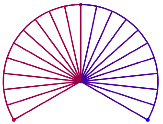
Abb. 10:

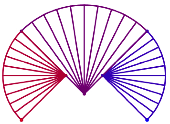
Abb. 11:

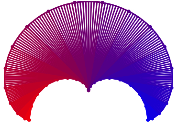
Abb. 12:

Es entsteht sowohl innen wie außen eine interessante Kurve. In der Abbildung 13 ist die Kurve durch approximiert. Zudem ist ein Referenzquadrat der Seitenlänge 4 eingezeichnet.

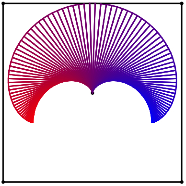
Abb. 13: Was für eine Kurve ist das?

Die Außenkurve hat natürlich dieselbe Länge wie die Zykloide, also 8. Sie ist die Evolvente der Innenkurve.

Die Länge der Innenkurve ist 4. Dies lässt sich leicht beweisen. Für ist die Innenkurve ein Polygonzug, dessen Streckenlängen die Differenzen aufeinander folgender sind. Die Gesamtlänge ist also:

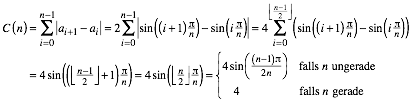
Somit ist:

Vermutung: Die halbe Innenkurve ist ähnlich zur halben Außenkurve (Drehstreckung, Drehung um , Streckfaktor 2).