Hans Walser, [20190330]
Archimedische Spirale
1 Worum geht es?
Es werden zwei falsche Grundvorstellungen im Kontext der archimedischen Spirale besprochen.
2 Die archimedische Spirale
Die Abbildung 1 zeigt die archimedische Spirale.
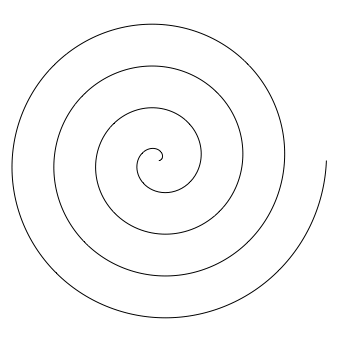
Abb. 1: Archimedische Spirale
Die archimedische Spirale hat die Parameterdarstellung:
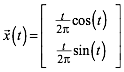 (1)
(1)
2.1 Gleichdick
Eine falsche Grundvorstellung ist die Annahme, die
archimedische Spirale sei berall ãgleich dickÒ. Der
Kreis, der sich einpassen lsst, habe berall den gleichen Durchmesser. Die
Abbildung 2 zeigt ein Gegenbeispiel (bestimmt mit CAS und DGS).
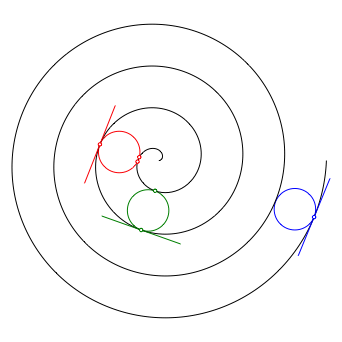
Abb.
2: Gleich gro§e Kreise
Es sind
drei gleich gro§e Kreise eingezeichnet, je mit dem Durchmesser 0.99. Die drei
Kreise berhren au§en die Spirale. Dies ist durch die jeweilige Tangente
angedeutet.
Der
innerste Kreis (rot) schneidet die Spirale auf der dem Berhrungspunkt gegenberliegenden
Seite in zwei Punkten. Er ist also fr das Einpassen an dieser Stelle zu gro§.
Der
u§erste Kreis (blau) berhrt schneidet die Spirale auf der Gegenseite nicht.
Er ist fr das Einpassen an dieser Stelle zu klein.
Nach dem
Zwischenwertsatz von Bolzano gibt es dazwischen eine Stelle, wo der Kreis auf
der Gegenseite gerade noch berhrt (grn).
Eine Figur, die insinuiert, eine Folge von gleichen Kreisen sei einer archimedischen Spirale eingepasst (Abb. 3), ist also gemogelt.
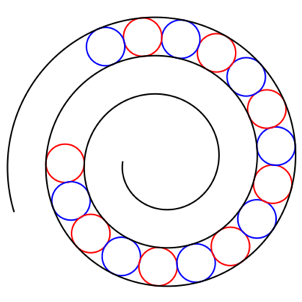
Abb. 3: Gemogelte Figur
Es ist ebenso prinzipiell falsch, ein aufgewickeltes Seil konstanter Dicke als archimedische Spirale zu modellieren (Abb. 4).

Abb. 4: Unsicheres Kletterseil
2.2 Arithmetische Folge
Die Abbildung 5 zeigt die archimedische Spirale gem§ der Parameterdarstellung (1), mit Farbwechseln.
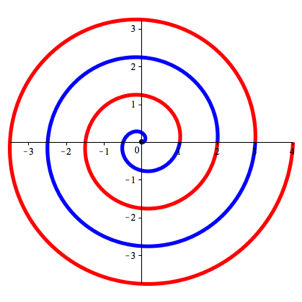
Abb. 5: Farbwechsel
Fr ![]() ergibt sich der erste Bogen (blau), fr
ergibt sich der erste Bogen (blau), fr ![]() der zweite Bogen (rot) und so
alternierend weiter.
der zweite Bogen (rot) und so
alternierend weiter.
Eine falsche Grundvorstellung ist die nun Annahme, die
jeweiligen Bogenlngen von Farbwechsel zu Farbwechsel bildeten eine
arithmetische Folge mit dem Zuwachs 2¹.
Dies kann numerisch widerlegt werden. Aus (1) ergibt sich das Bogenelement:
![]() (2)
(2)
Der n-te Bogen hat daher die Lnge:
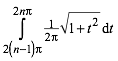 (3)
(3)
Die Tabelle 1 gibt die ersten numerischen Werte.
|
n |
Bogenlnge |
Zuwachs |
|
0 |
3.383044285 |
– |
|
1 |
9.479749375 |
6.096705090 |
|
2 |
15.74019423 |
6.260444855 |
|
3 |
22.01402936 |
6.27383513 |
|
4 |
28.29208540 |
6.27805604 |
|
5 |
34.57202478 |
6.27993938 |
|
6 |
40.85296955 |
6.28094477 |
|
7 |
47.13451475 |
6.28154520 |
|
8 |
53.41644718 |
6.28193243 |
|
9 |
59.69864408 |
6.28219690 |
|
10 |
65.98102985 |
6.28238577 |
|
11 |
72.26355480 |
6.28252495 |
|
12 |
78.54618558 |
6.28263078 |
|
13 |
84.82889878 |
6.28271320 |
|
14 |
91.11167695 |
6.28277817 |
|
15 |
97.39450765 |
6.28283070 |
|
16 |
103.6773804 |
6.28287275 |
|
17 |
109.9602912 |
6.2829108 |
|
18 |
116.2432306 |
6.2829394 |
|
19 |
122.5261956 |
6.2829650 |
|
20 |
128.8091822 |
6.2829866 |
Tab. 1: Bogenlngen und Zuwachs
Wir
sehen, dass der Zuwachs nicht
konstant ist. Wir haben daher keine
arithmetische Folge. Hingegen ist zu vermuten, dass sich der Zuwachs der Zahl ![]() annhert.
annhert.
3 Pseudoarchimedische Spiralen
Die beiden oben beschriebenen falschen Grundvorstellungen lassen sich mit pseudoarchimedischen Spiralen beheben. Diese sind aus Kreisbogen zusammengesetzt.
Dazu als Einstiegshilfe eine Kreisschar.
3.1 Kreisschar
Die Abbildung 6 zeigt eine quidistante Kreisschar.
Trivialerweise lassen sich Kreise mit dem Durchmesser 1 einpassen.
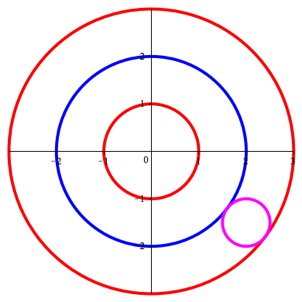
Abb. 6: Kreisschar
Da die
Radien von Kreis zu Kreis um eins zunehmen, nehmen die Umfnge um ![]() zu. Wir haben eine arithmetische Folge.
zu. Wir haben eine arithmetische Folge.
3.2 Pseudoarchimedische Spirale
Die
Abbildung 7 zeigt nun eine pseudoarchimedische Spirale. Sie ist aus Halbkreisen
zusammengesetzt. Die oberen Halbkreise haben den Punkt ![]() als Zentrum und echt halbzahlige Radien.
Die unteren Halbkreise haben den Koordinatenursprung als Zentrum um und
ganzzahlige Radien.
als Zentrum und echt halbzahlige Radien.
Die unteren Halbkreise haben den Koordinatenursprung als Zentrum um und
ganzzahlige Radien.
Der Abstand zwischen den Kurven ist eins, es lassen sich Kreise mit dem Durchmesser eins einpassen.
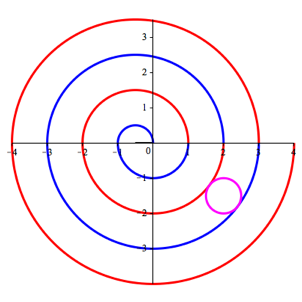
Abb. 7: Pseudoarchimedische Spirale aus Halbkreisen
Wir
berechnen die Bogenlngen von Farbwechsel zu Farbwechsel, oder anders gesagt zwischen
den Kurvenpunkten mit den Koordinaten ![]() .
Wir erhalten die Werte der Tabelle 2.
.
Wir erhalten die Werte der Tabelle 2.
|
n |
Farbe |
Bogenlnge |
Zuwachs |
|
0 |
blau |
|
|
|
1 |
rot |
|
|
|
2 |
blau |
|
|
|
3 |
rot |
|
|
Tab. 2: Bogenlngen und Zuwachs
Der
Zuwachs von Runde zu Runde ist ![]() .
Wieder eine arithmetische Folge.
.
Wieder eine arithmetische Folge.
Analoges gilt fr eine aus Drittelkreisen zusammengesetzte pseudoarchimedische Spirale (Abb. 8). Die Zentren sind die Eckpunkte des gelb eingezeichneten regelm§igen Dreieckes. Der Umfang dieses Dreieckes ist eins.
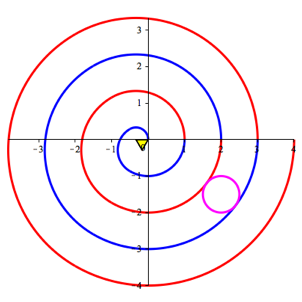
Abb. 8: Aus Drittelkreisen zusammengesetzt
Wir knnen die pseudoarchimedische Spirale entstanden denken wie folgt. Um das Dreieck wickeln wir einen (unendlich dnnen) Faden. Dann wickeln wir ihn wieder ab und zeichnen die Bahnkurve des Fadenendes.
Die Abbildung 9 zeigt die analoge aus Viertelkreisen zusammengesetzte pseudoarchimedische Spirale. Die Zentren der Viertelkreise sind die Ecken eines Quadrates mit dem Umfang eins.
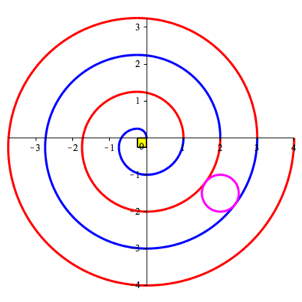
Abb. 9: Viertelkreise
Wir
knnen die Eckenzahl des regelm§igen Vieleckes im Zentrum beliebig erhhen.
Dabei soll der Umfang immer eins bleiben. Die Lngen der einzelnen Umlufe von
Farbwechsel zu Farbwechsel bilden eine arithmetische Folge mit dem Zuwachs ![]() .
Und wir knnen berall Kreise mit dem Durchmesser eins einpassen.
.
Und wir knnen berall Kreise mit dem Durchmesser eins einpassen.
Die
Abbildung 10 zeigt die Situation fr die Eckenzahl ![]() .
Wir haben im Zentrum einen gelben Kreis mit dem Umfang eins. Die Abwickelkurve
wird in diesem Kontext als Evolvente (oder
Involute) bezeichnet.
.
Wir haben im Zentrum einen gelben Kreis mit dem Umfang eins. Die Abwickelkurve
wird in diesem Kontext als Evolvente (oder
Involute) bezeichnet.
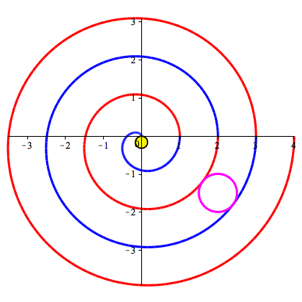
Abb. 10: Evolvente
Auf Grund
einer Grenzwertberlegung erhalten wir fr die Bogenlngen von Farbwechsel zu
Farbwechsel wiederum eine arithmetische Folge mit dem Zuwachs ![]() .
.
Wer der
Grenzwertberlegung nicht traut, ist zur Rechnung eingeladen. Die Evolvente der
Abbildung 10 hat mit ![]() folgende Parameterdarstellung:
folgende Parameterdarstellung:
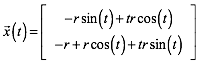 (4)
(4)
Fr ![]() ergibt sich der erste Bogen (blau), fr
ergibt sich der erste Bogen (blau), fr ![]() der zweite Bogen (rot) und so
alternierend weiter.
der zweite Bogen (rot) und so
alternierend weiter.
Ferner ist:
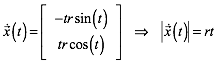 (5)
(5)
Fr das Bogenelement erhalten wir also:
![]() (6)
(6)
Der n-te Bogen hat daher die Lnge:
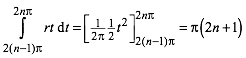 (7)
(7)
Das ist
eine arithmetische Folge mit dem Zuwachs ![]() .
.
Weblinks
Hans Walser: Evolvente
http://www.walser-h-m.ch/hans/Miniaturen/E/Evolvente/Evolvente.htm
Hans Walser: Karo-Spirale
http://www.walser-h-m.ch/hans/Miniaturen/K/Karospirale/Karospirale.htm