Hans Walser, [20201117]
Archimedische Spirale
1 Worum geht es?
€hnlichkeit der archimedischen Spiralen
2 Standardspirale und allgemeine Spirale
Die Parameterdarstellung
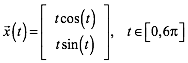 (1)
(1)
gibt die
archimedische Standardspirale der Abbildung 1a mit drei Windungen. Die obere
Grenze des Parameterintervalls kann natźrlich beliebig verŠndert werden. Bei
der Obergrenze ![]() haben wir n Windungen.
haben wir n Windungen.

Abb. 1: Standardspirale und allgemeine Spirale
Die Parameterdarstellung
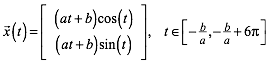 (2)
(2)
gibt die allgemeine Form der archimedischen Spirale mit drei Windungen (Abb. 1b fźr a = 0.6 und b = 1.4).
3 Transformation des Parameters
Mit
![]() (3)
(3)
kann (2) in der Form
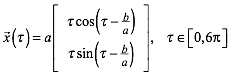 (4)
(4)
geschrieben werden.
4 Transformation der Spirale
Die durch (2) gegebene Spirale (Abb. 1b) dann durch eine Drehstreckung in die Standardspirale źberfźhrt werden. Dabei ist:
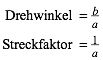 (5)
(5)
In der Abbildung 2b ist die Drehung gemŠ§ (5) durchgefźhrt (grźne Spirale). Wir sehen, dass Anfang und Ende im Vergleich mit der Standardspirale passend auf der x-Achse liegen. Die Grš§e stimmt noch nicht.

Abb. 2: Drehung
In der Abbildung 3b ist nun auch die Streckung gemŠ§ (5) vollzogen worden (blaue Spirale). Wir haben die Standardspirale erreicht.
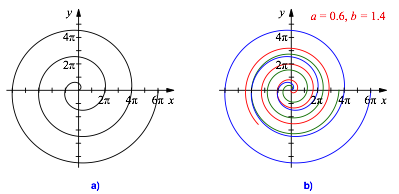
Abb. 3: Streckung
5 €hnlichkeit
Somit kann jede archimedische Spirale mit einer Drehstreckung auf die archimedische Standardspirale (mit gleicher Windungszahl) abgebildet werden. Daraus folgt aber, dass zwei beliebige archimedische Spiralen (mit gleicher Windungszahl) Šhnlich sind.
Es gibt also im Wesentlichen nur eine archimedische Spirale.
Bemerkung: Bei den logarithmischen Spiralen ist die Situation všllig anders. Da eine logarithmische Spirale einen vom Zentrum ausgehenden Strahl unter konstantem Winkel schneidet, gibt es zu jedem Schnittwinkel eine andere logarithmische Spirale. Zwei verschiedene logarithmische Spiralen sind nicht Šhnlich. Hingegen ist eine logarithmische Spirale zu sich selbst Šhnlich. Sie kann durch geeignete Drehstreckungen mit sich selber zur Deckung gebracht werden (dabei wir die Spirale unendlich lang gedacht). Diese SelbstŠhnlichkeit wiederum ist bei den archimedischen Spiralen nicht vorhanden.
Weblinks
Hans Walser: Lotschnittpunkt
http://www.walser-h-m.ch/hans/Miniaturen/L/Lotschnittpunkt2/Lotschnittpunkt2.htm
Hans Walser: Lotschnittpunkt
http://www.walser-h-m.ch/hans/Miniaturen/L/Lotschnittpunkt/Lotschnittpunkt.htm
Hans Walser: Archimedische Spirale
http://www.walser-h-m.ch/hans/Miniaturen/A/Arch_Spirale/Arch_Spirale.htm