Hans Walser, [20210724]

Archimedische Spirale und Tangenten

1 Worum geht es?

Zusammenhang zwischen Tangenten an archimedische Spiralen und Parabeltangenten

2 Schritt für Schritt

Wir beginnen mit einer Schar von gleichmäßig verdrehten archimedischen Spiralen (Abb. 1).

Abb. 1: Archimedische Spiralen

Ein vom Zentrum ausgehender Strahl wird von den Spiralen in gleichmäßigen Abständen geschnitten (Abb. 2).

Abb. 2: Gleichmäßig verteilte Schnittpunkte

Wir zeichnen nun in diesen Schnittpunkten die Tangenten an die jeweiligen Spiralen (Abb. 3).

Abb. 3: Tangenten

Die Tangenten sind nicht parallel. Sie werden gegen außen immer steiler.

Die Enveloppe dieser Tangenten ist eine Parabel (Abb. 4).

Abb. 4: Parabel

Die Normalen an die Spiralen in den Schnittpunkten verlaufen durch einen gemeinsamen Punkt (Abb. 5). Dieser ist der Brennpunkt der Parabel.

Abb. 5: Normalen und Brennpunkt

Nachweis durch Rechnen.

3 Animationen

Statt einer Schar von verdrehten archimedischen Spiralen können wir eine einzige Spirale abdrehen (Abb. 6).

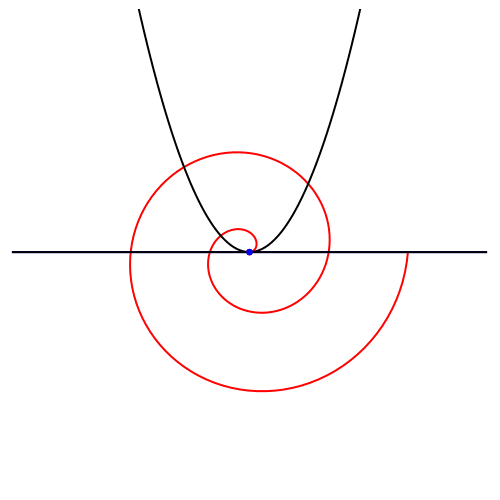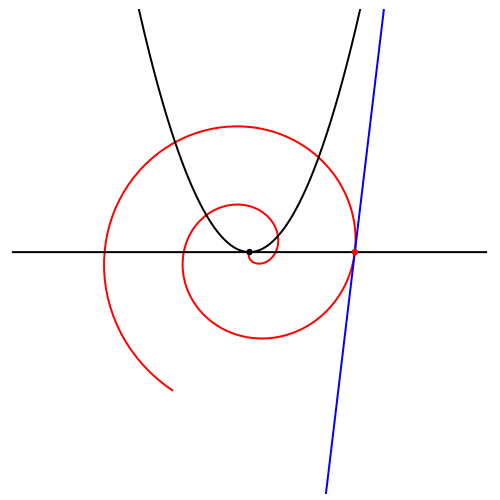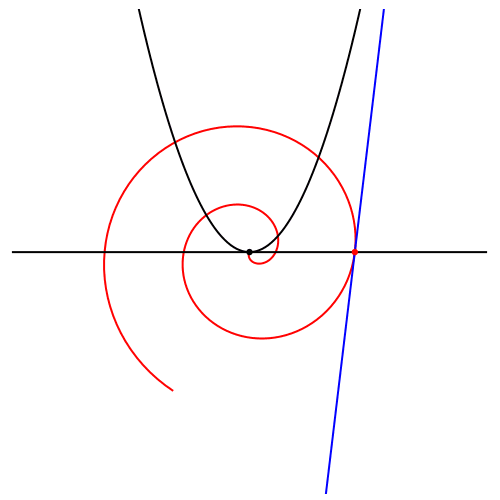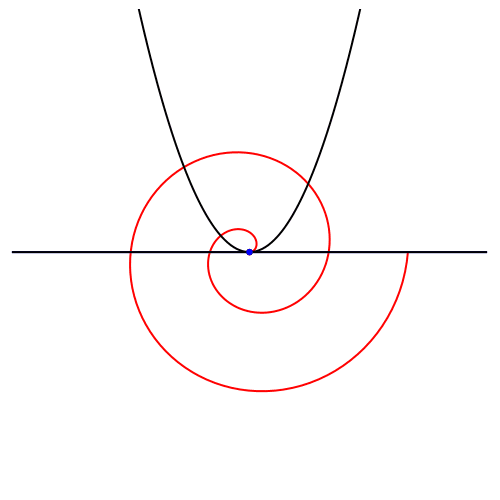
Abb. 6: Drehen der Spirale

In der Abbildung 7 ist auch die jeweilige Normale gegeben. Zudem wird auch der linke Ast der Parabel bewirtschaftet.

Abb. 7: Variante