Hans Walser, [20201125]
Aufwickel-Pythagoras
1 Worum geht es?
Kinematische Illustration des Satzes von Pythagoras mit archimedischen Spiralen. Der Focus wird dabei auf die Invarianz der Summe der Kathetenquadrate gelegt.
2 Pythagoras mit Kreisen
In der Pythagoras-Ikone zeichnen wir die Inkreise der Quadrate (Abb. 1). Nach dem Satz des Pythagoras ist die FlŠchensumme der beiden roten Kathetenkreise gleich dem FlŠcheninhalt des blauen Hypotenusenkreises.
Der Hypotenusenkreis ist gleich gro§ wie der Thaleskreis des Dreieckes.
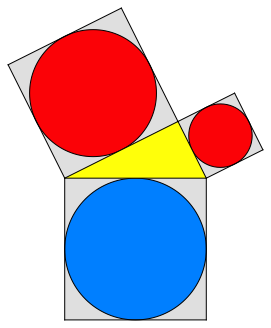
Abb. 1: Rot = blau
Die Animation 1 illustriert den Sachverhalt. Der flŠchenmŠ§igen Zunahme des einen roten Kreises entspricht eine Abnahme des anderen.

Animation 1: Rot = blau
3 Pythagoras mit Spiralen
Wir approximieren die roten Kreise durch Aufwickel-Spiralen (Abb. 2). Ich habe diese mit archimedischen Spiralen angenŠhert.
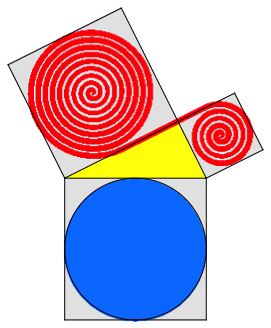
Abb. 2: Spiralen
Die Animation 2 zeigt das Auf- und Abwickeln. Dem entspricht das Wachsen und Abnehmen der roten KreisflŠchen.

Animation 2: Spiralen
4 Pythagoras in der Kugel
Nun hat aber die Figur der Abbildung 2 einen kleinen systematischen Fehler. Das gradlinige Verbindungsstźck der beiden Spiralen variiert beim Animationsprozess in der LŠnge. Die FlŠchenźbergabe von einer roten FlŠche in die andere ist also nicht gleichmŠ§ig.
Eine Lšsung des Problems besteht darin, das †bergangstźck auf einen Punkt zu schrumpfen. Dazu gehen wir in den Raum. Wir setzen die Kreisscheiben (vgl. Abb. 1) rechtwinklig an die Dreiecksebene an und zwar so, dass jede Dreiecksseite Durchmesser ihres Kreises wird (Abb. 3a). Die Gesamtfigur passt in eine Kugel mit demselben Durchmesser wie der Hypotenusenkreis (Abb. 3b). Das rechtwinklige Dreieck liegt in der Ebene des Nullmeridians. Der Hypotenusenkreis wird zum €quator.
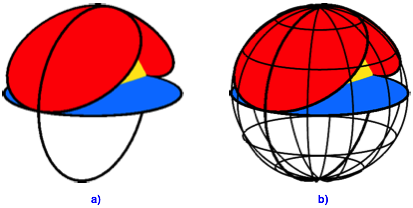
Abb. 3: Pythagoras-Kreisscheiben in der Kugel
Die Animation 3 illustriert den Sachverhalt.
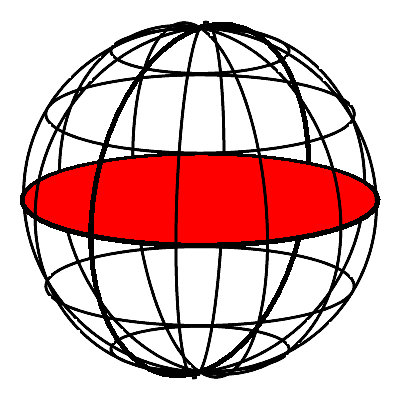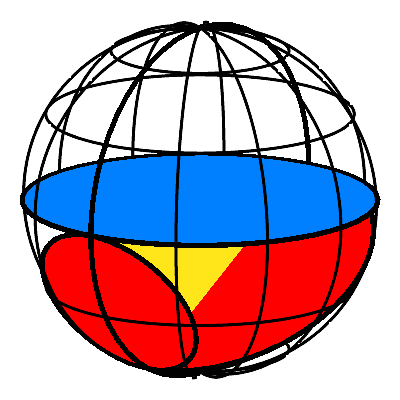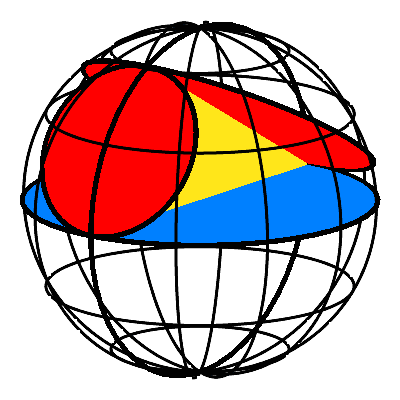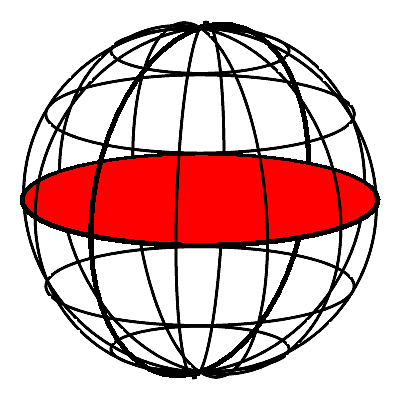
Animation 3: Pythagoras-Kreisscheiben in der Kugel
5 Spiralen in der Kugel
Wir kšnnen wieder die roten Kreise durch Spiralen ersetzen (Abb. 4). Der †bergangspunkt der beiden Spiralen ist bei der Dreiecksecke mit dem rechten Winkel.

Abb. 4: Spiralen
Die folgenden Animationen zeigen verschiedene Sichten.
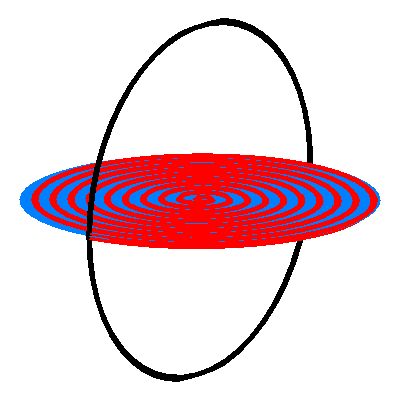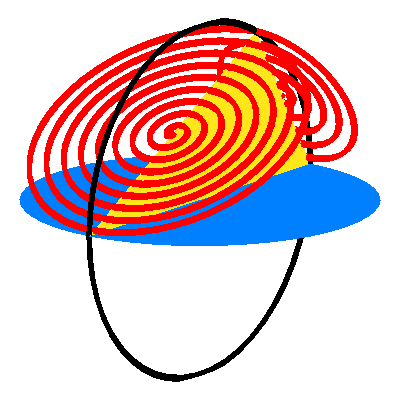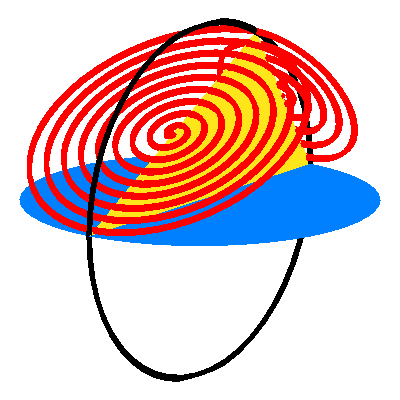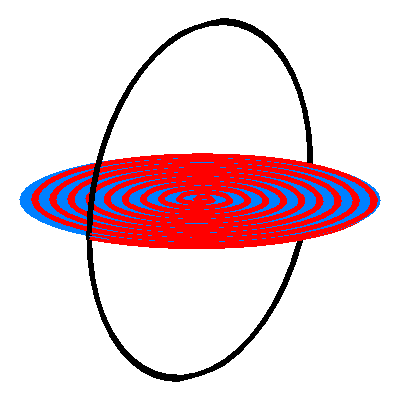
Animation 4: Ansicht
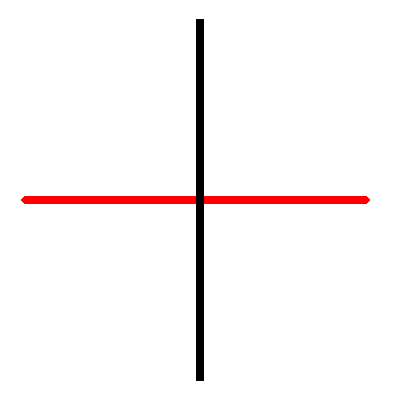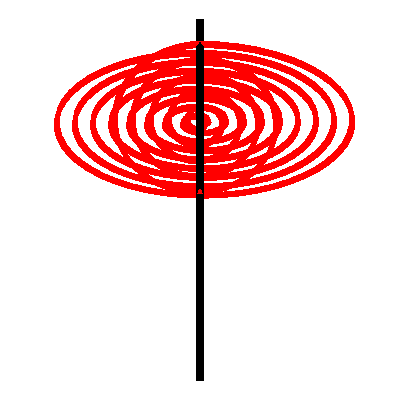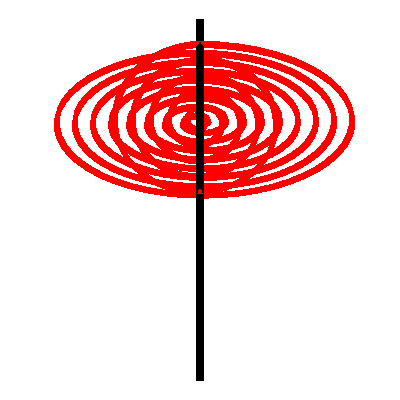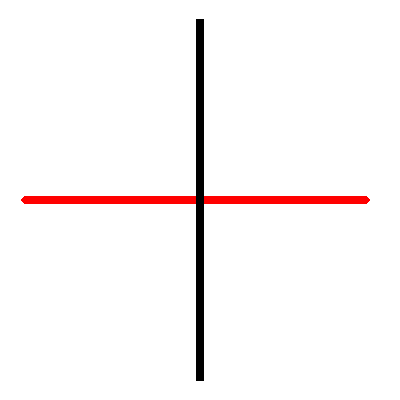
Animation 5: Sicht von vorne
Animation 6: Sicht von der Seite

Animation 7: Sicht von oben
Weblinks
Hans Walser: Pythagoras in der Kugel
http://www.walser-h-m.ch/hans/Miniaturen/P/Pythagoras_i_Kugel/Pythagoras_i_Kugel.htm
Hans Walser: Aufwickel-Pythagoras
http://www.walser-h-m.ch/hans/Miniaturen/A/Aufwickel-Pythagoras2/Aufwickel-Pythagoras2.htm
Hans Walser: Aufwickel-Pythagoras
http://www.walser-h-m.ch/hans/Miniaturen/A/Aufwickel-Pythagoras/Aufwickel-Pythagoras.htm