Hans Walser, [20240534]
Ausgebüxte n-Ecke
1 Worum es geht
Regelmäßige Vielecke, Symmetrie, Teilbarkeit
Schöne Figuren
2 Aus dem Fünfeck
Wir zeichnen ein regelmäßiges Fünfeck bis auf die letzte Seite (Abb. 1). Diese letzte Seite zeichnen wir nach außen.

Abb. 1: Fast vollständiges Fünfeck
Die nach außen ausgebüxte Seite ergänzen wir zu einem zweiten fast vollständigen Fünfeck (Abb. 2).

Abb. 2: Zweites Fünfeck
Entsprechend fahren wir fort (Abb. 3 und Abb. 4).

Abb. 3: Drittes Fünfeck
Es kommt zu Überschneidungen.

Abb. 4: Viertes Fünfeck
Nach insgesamt zehn Schritten schließt sich die Figur (Abb. 5).

Abb. 5: Schließungsfigur
3 Allgemein
Wir verfahren analog mit anderen fast vollständigen regelmäßigen n-Ecken (Abb. 6).

Abb. 6: Die ersten Beispiele
4 Anzahl Schritte
Die Anzahl s der Schritte bis zur Schließungsfigur variiert (Tab. 1). Wir erkennen aber eine Gesetzmäßigkeit.
|
n |
Anzahl Schritte s |
|
3 |
6 = 2•3 |
|
4 |
4 |
|
5 |
10 = 2•5 |
|
6 |
3 = ½ •6 |
|
7 |
14 = 2•7 |
|
8 |
8 |
|
9 |
18 = 2•9 |
|
10 |
5 = ½ •10 |
|
11 |
22 = 2•11 |
|
12 |
12 |
|
13 |
26 = 2•13 |
|
14 |
7 = ½ •14 |
|
15 |
30 = 2•15 |
|
16 |
16 |
|
17 |
34 = 2•17 |
|
18 |
9 = ½ •18 |
|
19 |
38 = 2•19 |
|
20 |
20 |
Tab. 1: Anzahl Schritte bis zur Schließungsfigur
Wir nehmen eine Fallunterscheidung vor je nach der Anzahl n der Ecken des Start-n-Eckes.
4.1 Ungerade Eckenzahl
Für ungerades n ist die Anzahl der Schritte das Doppelte der Eckenzahl.
4.2 Gerade Eckenzahl
4.2.1 Kein Vielfaches von 4
Die Anzahl der Schritte ist die Hälfte der Eckenzahl.
4.2.2 Vielfache von 4
Die Anzahl der Schritte ist gleich der Eckenzahl.
5 Verdichtung der Figur
Für gerade Eckenzahlen, die kein Vielfaches von 4 sind, fügen wir im Drehsinn mittig eine Kopie der Figur ein (Abb. 7 für n = 6, blaue Kopie).

Abb. 7: Verdichtung
Damit erhalten wir für sämtliche geraden n ein einheitliches Erscheinungsbild (Abb. 8, monochrom).
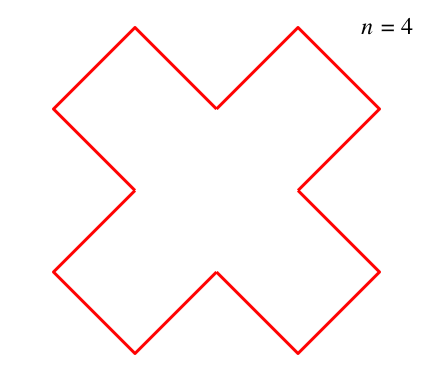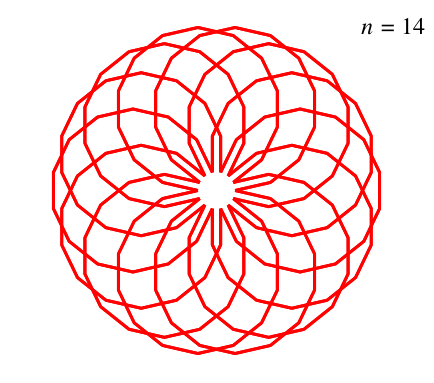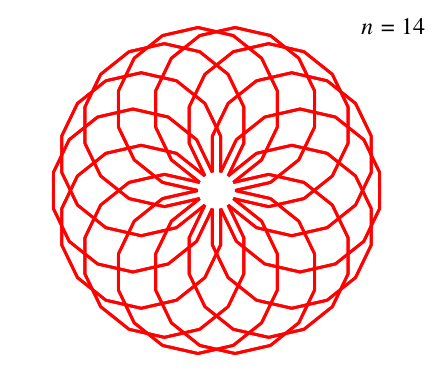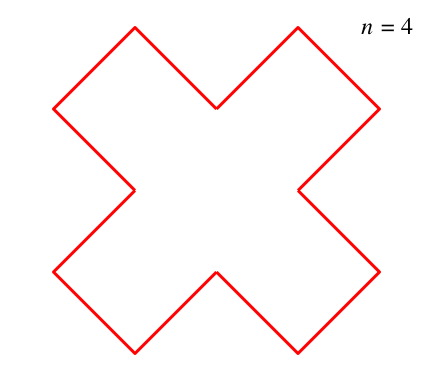
Abb. 8: Verdichtung
Schließlich können wir die teilweise bereits verdichteten Figuren mit geradem n weiter verdichten (Abb. 9 für n = 6).
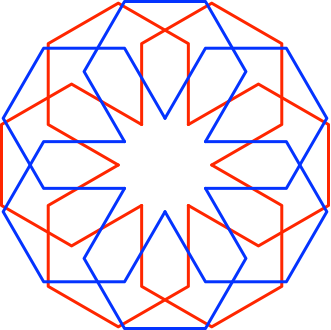
Abb. 9: Weitere Verdichtung
6 Einheitliches Erscheinungsbild
Damit erhalten wir ein einheitliches Erscheinungsbild für sämtliche n (Abb. 10). Im Zentrum ergibt sich jeweils ein Stern mit 2n Spitzen.

Abb. 10: Einheitliches Erscheinungsbild
Nun variiert allerdings die Anzahl der Schließungsfiguren in der Gesamtfigur (Tab. 2). Wir sehen aber eine Gesetzmäßigkeit.
|
n |
Anzahl Schließungsfiguren |
|
3 |
1 |
|
4 |
2 |
|
5 |
1 |
|
6 |
4 |
|
7 |
1 |
|
8 |
2 |
|
9 |
1 |
|
10 |
4 |
|
11 |
1 |
|
12 |
2 |
|
13 |
1 |
|
14 |
4 |
|
15 |
1 |
|
16 |
2 |
|
17 |
1 |
|
18 |
4 |
|
19 |
1 |
|
20 |
2 |
Tab. 2: Anzahl Schließungsfiguren