Hans Walser, [20201203]

Affinreguläres Vieleck

1 Worum geht es?

Ein Unterteilungsverfahren führt zu affinregulären Vielecken.

2 Das Verfahren

Wir arbeiten mit einem beliebigen n-Eck. Wir unterteilen die Seiten zyklisch im Verhältnis . Die Teilpunkte sind die Ecken des nachfolgenden n-Eckes (Abb. 1a). Dann iterieren wir den Prozess (Abb. 1b).

In der Abbildung 1 ist n = 5 und . Es sind außer dem Startfünfeck die ersten zehn nachfolgenden Fünfecke gezeichnet.

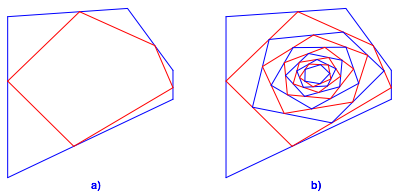
Abb. 1: Unterteilung der Seiten

3 Vermutung

Bei fortschreitender Iteration tendieren die n-Ecke gegen ein affinreguläres n-Eck, also ein affines (lineares) Bild eines regulären n-Eckes.

Die Abbildung 2 zeigt ein reguläres Fünfeck (grün) und ein affinreguläres Fünfeck (blau). Das innerste Fünfeck der Abbildung 1b entspricht schon recht gut diesem affinregulären Fünfeck.

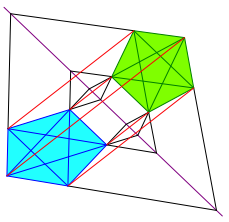
Abb. 2: Affinreguläres Fünfeck

Bei einer affinen Abbildung werden Längen und Winkel verzerrt.

Hingegen bleibt die Parallelität erhalten. Im affinregulären Fünfeck ist jede Diagonale parallel zur einer Seite wie im regulären Originalfünfeck.

Ebenso bleiben die Längenverhältnisse von parallelen Strecken erhalten. Jede Diagonale verhält sich zur parallelen Seite im Goldenen Schnitt (etwa 1.618) wie im Original.

Das affinreguläre Bild kann als Schatten bei Parallelbeleuchtung des regulären Originals gesehen werden.

4 Beweis fehlt

Einen allgemeinen Beweis für die Vermutung habe ich nicht.

5 Beispiele und Sonderfälle

5.1 Reguläres Startvieleck

Ist das Starvieleck regulär, sind es aus Symmetriegründen auch alle nachfolgenden Vielecke (Abb. 3 mit n = 7, und 50 Iterationen).

Abb. 3: Reguläres Startvieleck

5.2 Dreieck

Für erhalten wir eine Folge (längenmäßig eine abnehmende geometrische Folge) von zum Startdreieck ähnlichen Dreiecken (Abb. 4). Die Dreiecksflächen sind ebenfalls eine abnehmende geometrische Folge, mit dem Faktor .

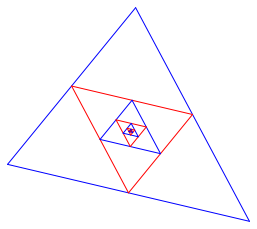
Abb. 4: Folge ähnlicher Dreiecke

Für erhalten wir eine alternierende Doppelfolge (Abb. 5).

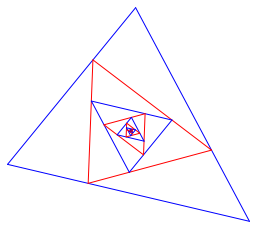
Abb. 5: Doppelfolge

Alle blauen Dreiecke sind ähnlich zum blauen Startdreieck. Sie gehen durch eine zentrische Streckung am Schwerpunkt des Startdreiecks mit dem Faktor auseinander hervor. Die Flächeninhalte werden also mit dem Faktor verkleinert.

Die roten Dreiecke bilden ebenfalls eine Folge ähnlicher Dreiecke mit denselben Verkleinerungen wie die blauen. Die roten und die blauen sind aber nicht ähnlich. Das erste rote Dreieck ist flächenmäßig ein Drittel des blauen Startdreieckes. Beweis dieser Sachverhalte siehe [1].

Für andere Teilverhältnisse sind keine Folgen erkennbar (Abb. 6).

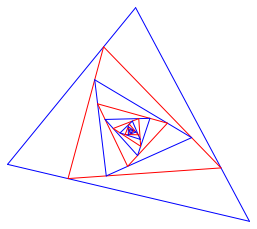
Abb. 6: Allgemeiner Fall

Da alle Dreiecke affin regulär sind, ist die Vermutung trivialerweise erfüllt. Wir brauchen keine Grenzfigur-Überlegung.

5.3 Viereck

Für ist bereits das erste Folgeviereck ein Parallelogramm, also affin regulär (Abb. 7). Dies ist der Satz von Varignon (1710) (Pierre de Varignon 1654-1722).

Wir erhalten zwei alternierende Folgen von zueinander ähnlichen Parallelogrammen. Der Flächeninhalt aufeinanderfolgender Vierecke wird jeweils halbiert.

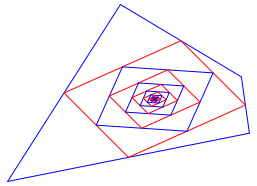
Abb. 7: Satz von Varignon

Wenn die Parallelogramme Quadrate sein sollen, muss das Startviereck zwei orthogonale und gleich lange Diagonalen haben (Abb. 8, [2]).

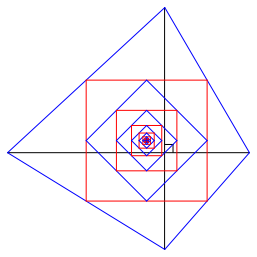
Abb. 8: Sonderfall mit Quadraten

Im allgemeinen Fall sind die Vierecke keine Parallelogramme, nähern sich aber einem solchen an (Abb. 9 mit ).

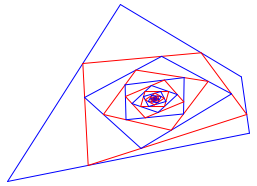
Abb. 9: Allgemeiner Fall

5.4 Fünfeck

Für lässt sich aus Walser (2000) ein Beweis ableiten. Für den allgemeinen Fall habe ich keinen Beweis.

5.5 Strahle und Spiralen

Die Abbildung 10 zeigt den optischen Effekt der Veränderung des Teilverhältnisses .

Abb. 10.1: Lambda = 0.5

Abb. 10.2: Lambda = 0.45

Abb. 10.3: Lambda = 0.4

Literatur

Walser, Hans (2000): Pascal-Türme. MNU. Der mathematische und naturwissenschaftliche Unterricht. 53/1 (15.1.2000), S. 12 – 17

Websites

[1] Hans Walser: Dreieck Dritteln

http://www.walser-h-m.ch/hans/Miniaturen/D/Dreieck_dritteln/Dreieck_dritteln.htm

[2] Hans Walser: Orthogonale Diagonalen

http://www.walser-h-m.ch/hans/Miniaturen/O/Orthogonale_Diagonalen/Orthogonale_Diagonalen.htm