Hans Walser, [20220704]

arctan

1 Worum geht es?

Eine Serie von Beweisen ohne Worte.

2 Beispiele

Es wird jeweils die Formel angeschrieben und anschließend der Beweis ohne Worte.

2.2

2.3

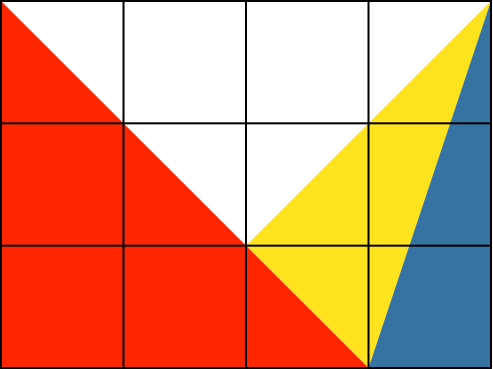
2.4

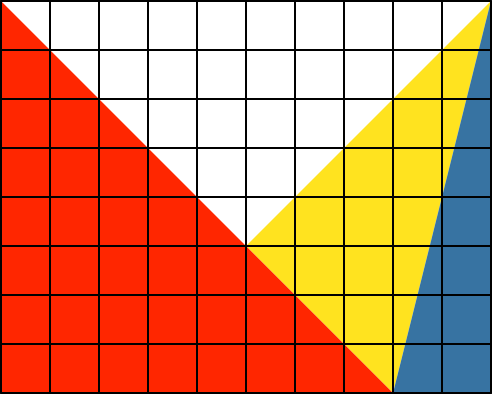
2.5

2.6

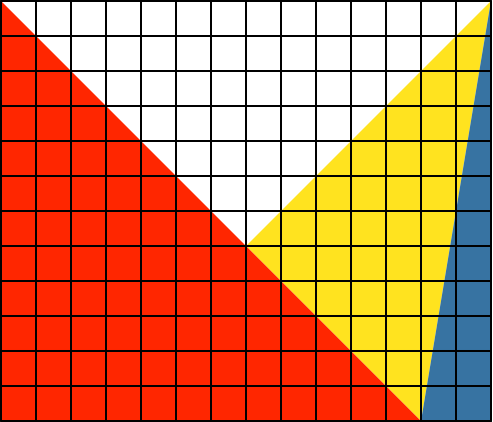
2.7

2.8

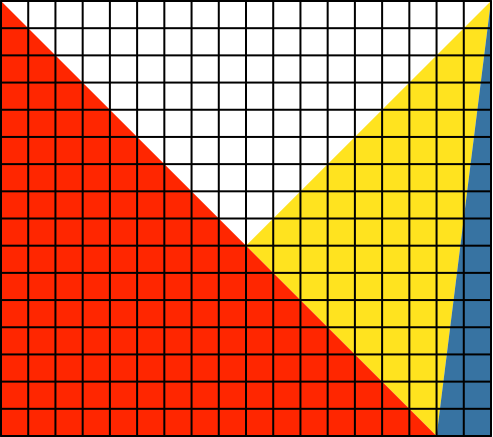
2.9

3 Allgemein

Allgemein gilt:

4 Beweis

Der Beweis erfolgt rechnerisch mit den Additionstheoremen des Tangens. Zunächst ist:

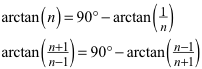
Eingesetzt in die zu beweisende Formel ergibt:

Auf Grund des Additionstheorems für den Tangens ist:

Daraus folgt die zu beweisende Formel.

Wie aus dem Beweis ersichtlich ist, kann n durch eine beliebige reelle Zahl größer als 1 ersetzt werden.

5 Bemerkungen

5.1 Paritätsproblem

Wir sehen sowohl bei den Formeln wie bei den Figuren ein unterschiedliches Verhalten bezüglich der Parität von n. Bei ungeradem n ist das Rechteck n Einheiten hoch, bei geradem n aber 2n Einheiten.

5.2 Grenzfigur

Für wachsendes n verschwindet das blaue Dreieck und wir erhalten die nachfolgende Grenzfigur.

Grenzfigur

Wegen

erhalten wir die zugehörige Formel:

Literatur

Alsina, Claudi & Nelsen, Roger B. (2013): Bezaubernde Beweise: eine Reise durch die Eleganz der Mathematik. Berlin: Springer Spektrum.

Nelsen, Roger B. (2000): Proofs without Words. MAA, The Mathematical Association of America. ISBN 978-0883857007

Weblink

Hans Walser: Tetraeder in Halbkugel

http://www.walser-h-m.ch/hans/Miniaturen/T/Tetraeder_in_Halbkugel/Tetraeder_in_Halbkugel.html